Mutlak Değer

Bir sayının, sayı doğrusunda başlangıç noktasına olan uzaklığına, bu sayının mutlak değeri denir.

\[ |a| = \begin{cases} a & \text{, } a \geq 0 \\ -a & \text{, } a < 0 \end{cases} \]

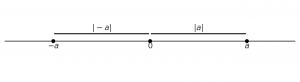
Örnek:

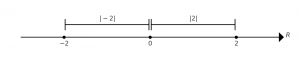
$$ |2| = 2 \quad, 2 > 0 \quad\text{olduğu için} $$

$$|-2| =- (- 2) \quad, -2 < 0 \quad \text{olduğu için} $$

Uyarı:

Mutlak değer ve çift kuvvetten köklü ifade negatif değer alamaz.

$$ \sqrt[2n]{ a^{2n} } = |a | ≥ 0 \quad (n \in Z^+)$$

$$ |x | ≥ 0 \; , \sqrt{ x} ≥ 0 \;, \sqrt[4]{x } \cdots \text{gibi} $$

Örnekler:

$ \bullet \quad a<b \; \text{ise } a-b<0 \; \text{olduğundan } \quad | a-b| = – (a-b) = b-a $ olur

$ \bullet \quad a<b< 0 \; \text{ise } a+b<0 \; \text{olduğundan } \quad | a+b| = – (a+b) =-a-b $ olur

$ \bullet \quad |x| + 2 > 0 \quad \text{olduğundan } |\;|x|\;+\; 2 | = |x|\;+ \;2$ olur

Mutlak Değerin Özellikleri:

$ 1). \; | \;a\;| = | \;-a\; | \quad ( \;| \;a\;-\;b\; | = | \;b\;- \;a\; | \;) $

$ 2). \; | \;a\; \cdot b\;| = | \;a\; | \cdot | \;b\; | $

$ 3). \; \large{\left| \frac{a}{b} \right| = \frac{|a|}{|b|} } \quad b\neq0 $

$ 4). \; \left| \; a^n\; \right| = \left| \; a \; \right|^n$

$ 5). \; \sqrt[2n]{a^{2n} } = \left| \; a\; \right| \quad n \in Z^+$

Soru 1

\[ a < 0 < b \;\text{ise} | a-b | – | a | + | b | \] ifadesinin eşiti nedir?

\[
\text{A) } a \quad
\text{B) } 2a \quad
\text{C) } 0 \quad
\text{D) } b \quad
\text{E) } 2b
\]

Çözüm:

$ a\; < \; b $ ise $ a \;- \; b\; < \; 0 $ olduğundan, $ |a – b | = – ( a- b) = -a + b $ ,

$ a < 0$ olduğundan $ |a | = -a $ , $ b > 0$ olduğundan $ |b | = b $ dir. Buradan

$$ |a\; -\; b | \;-\; |\;a\; | + | \;b\; |= -a + b\; – \;(\;-a) + b= 2b $$

$\textbf{Cevab: E} $

Soru 2

\[ a = 2 \sqrt{2 } – 3 \quad \text{ise } \quad \frac{\sqrt[4]{ a^4} \; + \; \sqrt[3]{ (-a)^3} }{\sqrt[3]{ a^3} } \;- \;a -1 \] işleminin sonucu nedir?

\[
\text{A) } 0 \quad
\text{B) } -1 \quad
\text{C) } 1 \quad
\text{D) } -2 \sqrt{2 } \quad
\text{E) } 2 \sqrt{2 }
\]

Çözüm:

$$ \frac{ \sqrt[4]{ a^4} \;+\;\sqrt[3]{ (-a)^3} } {\sqrt[3]{ a^3} }\; -a\;-\; 1 = \frac{ |a | \;-\; a }{a}\; -\;a \;-\;1$$

$$ a = 2 \sqrt{2 } – 3 \quad \text{olduğundan } |a | = – a $$

$$ =\frac{ -a -a}{a} -a -1 $$

$$ = -2 -a -1 $$

$$ = -2 -(2 \sqrt{2 }-3 ) -1 $$

$$ = -2 \sqrt{2 } $$

$\textbf{Cevab: D} $

Soru 3

\[ a < b < 0 \;\;\;\; \text{ise } \;\; | a\;+\; | a \;+\;b| \;| \;-\; |a| + b \] işleminin sonucu nedir?

\[
\text{A) } a \quad
\text{B) } -a \quad
\text{C) } b \quad
\text{D) } -b \quad
\text{E) } 0
\]

Çözüm:

$ a <0 $ olduğundan $ | a | = -a , \;\;$

$ a<0, \;\; $ ve $ b < 0 \;\;$ için $a + b < 0 $ olduğundan

$$ |a + b | = – (a+b) = -a-b \quad \text{dir. Buradan, } $$

$$ |a + |a+b| – |a|+ b = | a-a-b| – (-a) + b$$

$$ = |-b | + a + b$$

$b < 0 $ ise $-b>0 $ olduğundan $ |-b | = -b$ dir. Buna göre, $ = -b + a + b =a $ olur.

$\textbf{Cevab: A} $

Soru 4

\[ x \neq 1, x =< -\frac{1}{2}, \quad \frac{\sqrt{ 4x^2+ 4x + 1} \; + \; x }{-1 \;+\; \sqrt{ x^2} } \] işleminin sonucu nedir?

\[
\text{A) } -x \quad
\text{B) } x \quad
\text{C) } -1 \quad
\text{D) } 1 \quad
\text{E) } 2
\]

Çözüm:

$$= \frac{\sqrt{ 4x^2+ 4x + 1} \; + \; x }{-1 \;+\; \sqrt{ x^2} } = \frac{ \sqrt{ (2x + 1)^2} +x }{-1 + |x |} $$

$$ = \frac{| 2x +1 | + x }{-1 + | x|} $$

$$x < -\frac{1}{2} \quad \text{için } 2x \; + \; 1 < 0 \quad \text{olduğundan } $$

$$= \frac{-(2x +1 ) + x }{-1 \;+\; (-x)} $$

$$ = \frac{-2x – 1 + x }{ -1 -x } = 1 $$

$\textbf{Cevab: D} $

Soru 5

\[ a < | a | \quad \text{ve } b < a \quad \text{ise } \frac{ \sqrt[7]{ a^7} } {a }\; + \; \frac{ \sqrt[4]{ b^4} } {b }\; – \;\frac{ \sqrt{ a^3 b} } {ab } \] ifadesinin eşiti nedir?

\[
\text{A) } 1 \quad
\text{B) } 0 \quad
\text{C) } -1 \quad
\text{D) } -a \quad
\text{E) } a
\]

Çözüm:

$a < |a | $ ise $a < 0 $ ve $ b< a $ olduğundan $ b < 0 $ dır.

$$= \frac{ \sqrt[7]{ a^7} } {a }\; + \; \frac{ \sqrt[4]{ b^4} } {b }\; – \;\frac{ \sqrt{ a^3 b} } {ab } $$

$$= \frac{a}{a} + \frac{|b|}{b} – \;\frac{ \sqrt{ a^3 b} } {ab } = 1 + \frac{-b}{b} – \sqrt{a^2 } $$

$$= 1 – 1 – |a | $$

$$= -\; (-a ) = a $$

$\textbf{Cevab: E} $

Soru 6

\[ A = 7 + \frac{ | a| + |b | }{|a-b|} \] ise A nın alabileceği en küçük değer kaçtır?

\[
\text{A) } 7 \quad
\text{B) } 8 \quad
\text{C) } 9 \quad
\text{D) } 10 \quad
\text{E) } 11
\]

Çözüm:

$$ |\; a\; -\; b| ≤ |a |\; + \;|b | \Rightarrow \frac{|a\;-\; b|}{|a\;- \;b|} ≤ \frac{|a |\; + \;|b |}{|a\;-\; b|} $$

$$ \Rightarrow 1 ≤ \frac{|a | \;+\; |b | }{| a\;- \;b |} $$

Buradan $$ = \frac{|a| \;+ |\;b | }{| a \;- \;b|} $$ ifadesinin en küçük değeri 1 olacağından, A nın en küçük değeri

$$ 7\;+\;1 =8 \;\;\; \text{dir. } $$

$\textbf{Cevab: B} $