Ters Orantı
İki çokluktan biri artarken diğeri de ayni oranda azalıyorsa veya biri azalırken diğeri de ayni oranda artıyorsa bu iki çokluk ters orantılıdır denir.
Ters orantılı iki çokluğun çarpımı sabittir. \(y, x \) ile ters orantılı ise,
\[ y \cdot x = k \quad \text{veya } \quad y= \frac{k}{ x } \quad \text{tir. } \]
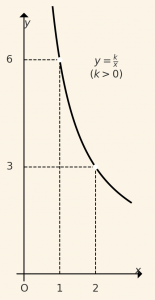
\[ y \cdot x = k \Rightarrow 6 \cdot 1 = 3 \cdot 2\]
\[ k= 6\]
Örnek:
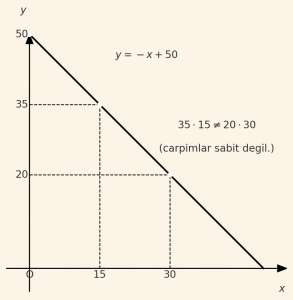
\( y= -x +50 \) ise \( x = 15 \) için \( y = 35 \)
\( x = 30 \) için \( y = 20 \)
burada x iki katına çıkarken y yarına inmediğinden \( y, x \) ile ters orantılı değildir.
Uyarı:
\( y, x \) ile doğru ve z ile ters orantılı ise
\[ y= \frac{k \cdot x }{z} \]
şeklinde yazılır.
Soru 1
Ali elindeki cevizleri, üç kardeşine küçükten büyüğe doğru sırasıyla 2, 3 ve 4 sayıları ile doğru orantılı olarak paylaştırmıştır. Ortanca kardeşi, diğer iki kardeşinin aldığı cevizlerin toplamından 90 ceviz eksik almıştır.
Buna göre, Ali’nin paylaştırdığı ceviz sayısı kaçtır?
\[
\text{A)} 250 \quad
\text{B) } 260 \quad
\text{C) } 270 \quad
\text{D) } 280 \quad
\text{E) } 290
\]
Çözüm:
Ali’nin kardeşlerinin aldığı cevizlerin sayısı sırasıyla
\( x = 2k, \; y = 3k \) ve \( z= 4k \) olsun. Ortanca kardeşin aldığı cevizlerin sayısı, diğer iki kardeşin aldığı cevizlerin sayısının toplamından 90 eksik olduğuna göre
\[ 3k = 2k+ 4k\; – \; 90 \Rightarrow k =30 \] bulunur. Buna göre toplam ceviz sayısı
\[x + y + z = 2k + 3k + 4k = 9k= 9 \cdot 30=270 \]
\(\textbf{Cevab: C} \)
Soru 2
380 sayısı, biri 3 ile diğeri 5 ile ters orantılı, üçüncüsü de 2 ile doğru orantılı üç sayıya ayrılırsa, en büyük sayı ile en küçük sayının farkı ne olur?
\[
\text{A)} 230 \quad
\text{B) } 240 \quad
\text{C) } 250 \quad
\text{D) } 260 \quad
\text{E) } 270
\]
Çözüm:
Sayılar sırasıyla \(x, y \) ve \(z\) olsun.
\[ x = \frac{k}{3} , \; y= \frac{k}{5} \quad \text{ve } \quad z = 2k \]
\[x + y+ z = 380 \Rightarrow \frac{k}{3} + \frac{k}{5} + 2k = 380 \Rightarrow k = 150 \]
\[y = \frac{k}{5} = \frac{150}{5} = 30, \quad z= 2k = 2 \cdot 150 =300 \quad \text{dür. } \]
Buna göre \(z- y= 300 \; – \;30 =270 \) dir
\(\textbf{Cevab: E} \)
Soru 3
Birbirini çeviren üç çarktaki toplam diş sayısı 165 tir. Birinci çark 2 devir yapınca ikinci çark 5, üçüncü çark 8 devir yapmaktadır. Buna göre ikinci çarkın diş sayısı kaçtır?
\[
\text{A)} 40 \quad
\text{B) } 45 \quad
\text{C) } 50 \quad
\text{D) } 55 \quad
\text{E) } 60
\]
Çözüm:
Birinci, ikinci ve üçüncü çarkın diş sayıları sırasıyla \( x, y \) ve \( z \) olsun. Diş sayısı ile devir sayısı ters orantılı olduğundan,
\[ x = \frac{k}{2}, \quad y= \frac{k}{5}, \quad z =\frac{k}{8} \] şeklinde yazılırsa,
\[x + y + z = 165 \Rightarrow \frac{k}{2} + \frac{k}{5} + \frac{k}{8} = 165 \]
\[\Rightarrow k = 200 \quad \text{ve } y = \frac{200}{5} = 40 \]
\(\textbf{Cevab: A} \)
Soru 4
Bir a sayısı \( (a- 1) \) ile doğru. \( (b + 1)^2 \) ile ters orantılıdır. \( a=2 \) iken \( b = – 2 \) oluyorsa, \(b = 1 \) iken a nedir?
\[
\text{A)} -1 \quad
\text{B) } 1 \quad
\text{C) } 2 \quad
\text{D) } 3 \quad
\text{E) } 4
\]
Çözüm:
\[ a = \frac{k \cdot (a-1 )}{(b+1)^2} \Rightarrow a= 2, \;\; \text{için} \ b= -2 \quad \text{oluyorsa} \]
\[ \quad 2 = \frac{k \cdot (2-1)}{(-2+1)^2} \]
\[ \Rightarrow k= 2 \quad \text{bulunur. } \]
\[ b= 1 \quad \text{için} \quad a= \frac{2 \cdot (a-1 )}{(1+1)^2} \Rightarrow 4a = 2a – 2 \]
\[ \Rightarrow a =-1 \]
\(\textbf{Cevab: A} \)
Problemlerde Orantı Kurulurken İzlenecek Yol:
Orantı problemlerinde aynı cins çokluklar alt alta gelecek sekilde yazılır. Daha sonra orantıların cinsi tespit edilir. Doğru orantı için çapraz, ters orantı için paralel oklar çizilir. Oklar yönünde çarpma yapılıp bulunan iki çarpım birbirine eşitlenir.
Soru 5
Mustafa, 800 sayfalık bir kitabın 300 sayfasını 12 günde okumuştur. Buna göre Mustafa, bu kitabın tamamını kaç günde okuyabilir?
\[
\text{A)} 24 \quad
\text{B) } 26 \quad
\text{C) } 28 \quad
\text{D) } 30 \quad
\text{E) } 32
\]
Çözüm:
\[
\begin{aligned}
&\text{12 günde} \quad \quad \quad\quad 300 \ \text{sayfa okursa} \quad \quad \quad \quad \quad \quad \\[1cm]
&\text{x günde} \quad \quad\quad\quad 800 \ \text{sayfa okur} \quad \quad \quad \quad \quad \quad \quad \\[1cm]
\hline \\[0.3cm]
&\textbf{Doğru orantı}
\end{aligned}
\]
Gün sayısı arttıkça okunan sayfa sayısı da ayni oranda artar. Bu nedenle doğru orantı var. Buna göre
\[ 12 \cdot 800 = x \cdot 300 \Rightarrow x = 32 \]
\(\textbf{Cevab: E} \)
Soru 5
300 tane askere 6 ay yetecek kadar yiyecek vardır. 100 tane asker terhis olursa, bu yiyecek kalan askerlere kaç ay yeter?
\[
\text{A)} 7 \quad
\text{B) } 8 \quad
\text{C) } 9 \quad
\text{D) } 10 \quad
\text{E) } 11
\]
Çözüm:
\[
\begin{aligned}
&\text{300 tane Askere } \quad \quad \quad\quad 6 \ \text{ ay yeterse} \quad \quad \quad \quad \quad \quad \\[1cm]
&\text{200 tane Askere } \quad \quad\quad\quad x \ \text{ ay yeter } \quad \quad \quad \quad \quad \quad \quad \\[1cm]
\hline \\[0.3cm]
&\textbf{Ters orantı}
\end{aligned}
\]
Asker sayısı arttıkça, yiyeceğin bitme süresi ayni oranda azalır. Bu nedenle ters orantı var. Buna göre
\[ 300 \cdot 6 = 200 \cdot x \Rightarrow x = 9\]
\(\textbf{Cevab: C} \)
Soru 6
\(4 \) isçi \(3 \) gün çalışarak \(24\; m^2\) halı dokuyabiliyor. \(5 \) isçi \(2 \) gün çalışarak kaç \( m^2\) halı okuyabilir?
\[
\text{A)} 10 \quad
\text{B) } 12 \quad
\text{C) } 18 \quad
\text{D) } 20 \quad
\text{E) } 24
\]
Çözüm:
\[
\begin{aligned}
&4 \; \text{ işçi } \quad \quad \quad\quad 3 \ \text{ gün çalışarak } \quad \quad \quad 24 \; \; m^2 \ \text{ gün çalışarak } \quad \quad \quad \\[1cm]
&5 \;\text{işçi } \quad \quad\quad\quad 2\ \text{ gün çalışarak } \quad \quad \quad \quad x \;\; m^2\text{ gün çalışarak } \quad \quad \quad \\[1cm]
\hline \\[0.3cm]
&\textbf{Ters orantı Doğru Orantı}
\end{aligned}
\]
işçi sayısı arttıkça işin bitme süresi de ayni oranda azalır. Çalısılan gün sayısı arttıkça dokunan halı miktarı da ayni oranda artar. Bu nedenle isçi sayısı ile çalışılan süre arasında ters orantı, çalısılan süre ile yapılan iş arasında ise doğru orantı vardır. Buna göre,
\[4 \cdot 3 \cdot x = 5 \cdot 2 \cdot 24 \Rightarrow x= 20 \; m^2 \; \text{dir. } \]
\(\textbf{Cevab: D} \)
← Önceki Sayfa | Sonraki Sayfa →