Birinci Dereceden İki Bilinmeyenli Denklemler
\( a,\; b, \; c \in R\) ve \(a \neq 0, \; b \neq 0\) olmak üzere, \(ax + by + c = 0 \) şeklindeki denklemlere birinci dereceden iki bilinmeyenIi denklemler denir.
\(ax + by + c = 0 \) şeklindeki bir denklemi sağlayan \( (x, y) \) ikililerinin kümesi analitik düzlemde bir doğru belirtir ve bu doğru üzerinde sonsuz nokta vardır. Bundan dolayı, birinci dereceden iki bilinmeyenli bir denklemin çözüm kümesi sonsuz elemanlıdır.
Örnek:
\( 2x + 3y-7 = 0 \) denkleminde \( x= t \) dönüşümü yapılırsa
\[2x + 3y -7= 0 \Rightarrow 2t+ 3y -7 = 0 \]
\[\Rightarrow y = \frac{7-2t}{3} \] olur. Buradan \( t \in R \) olmak üzere verilen denklemi sağlayan \( t, \frac{7-2t}{3} \) gibi sonsuz ikilinin var olduğu görülür.
Birinci Dereceden iki Bilinmeyenli Denklem Sistemi:
\[ a_1x +b_1y+c_1=0\]
\[ a_2x +b_2y+c_2=0\]
şeklindeki iki denklemden meydana gelen sisteme, birinci dereceden iki bilinmeyenli denklem sistemi denir.
Çözüm Kümesinin Bulunmasi:
\[ d1: \;\; a_1x +b_1y+c_1=0\]
\[d2: \;\; a_2x +b_2y+c_2=0\]
denklemleri, analitik düzlemde d1 ve d2 doğrularını belirtmek üzere, birinci dereceden iki bilinmeyenli bir denklem sisteminin çözümü için üç durum söz konusudur:
1. Durum
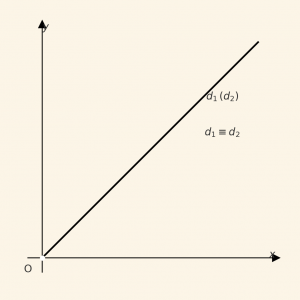
\[ \;\; \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\] ise denklem sisteminin çözüm kümesi sonsuz elemanlıdır. Çünkü bu durumda doğrular çakışıktır. Çakışık doğrular üzerindeki bütün noktalar (denklemleri sağlayan her \((x, y)\) ikilisi) çözüm kümesinin elemanlardır.
\[ 1) \;\; \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} \Rightarrow d_1 \equiv d_2\] ise sonsuz çözüm vardır.
Soru 12
\[ abx-2y -3 =0 \]
\[ 2x+4y-b=0 \]
denklem sisteminin çözüm kümesi sonsuz elemanlı ise a kaçtır?
\[
\text{A)} \frac{1}{6} \quad
\text{B) } \frac{1}{3} \quad
\text{C) } \frac{1}{2} \quad
\text{D) } 1 \quad
\text{E) } 2
\]
Çözüm:
Çözüm kümesinin sonsuz elemanlı olması için
\[ \frac{ab}{2} = \frac{-2}{4} =\frac{-3}{-b} \Rightarrow \frac{-2}{4} = \frac{-3}{-b} \Rightarrow b = -6 \]
ve
\[ \frac{ab}{2} = \frac{-2}{4} \Rightarrow a = \frac{1}{6} \]
\(\textbf{Cevab: A} \)
2. Durum
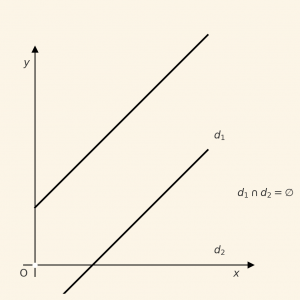
\[ \;\; \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}\] ise denklem sisteminin çözüm kümesi boş kümedir. Çünkü bu durumda doğrular paraleldir. Paralel doğrular kesişmeyeceğinden dolayı ortak noktaları yoktur.
\[ 1) \;\; \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2} \Rightarrow d_1 // d_2\] ise \[Ç = Ø\]
Soru 13
\[ x + ay + 5 =0 \]
\[ (a-2)x-y-4=0 \]
denklem sisteminin çözüm kümesi boş küme ise a kaçtır?
\[
\text{A)} -2\quad
\text{B) } -1\quad
\text{C) } 0 \quad
\text{D) } 1 \quad
\text{E) } 2
\]
Çözüm:
Çözüm kümesinin sonsuz elemanlı olması için
\[ \frac{1}{a-2} = \frac{a}{-1} \neq \frac{-5}{-4} \]
\[ \Rightarrow -1 = (a-2) \cdot a \]
\[ \Rightarrow a^2 – 2a + 1= 0 \]
\[ \Rightarrow a = 1 \]
\(\textbf{Cevab: D} \)
3. Durum
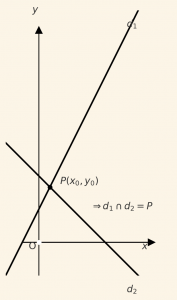
\[ \;\; \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \] ise denklem sisteminin çözüm kümesi tek elemanlıdır. Çünkü bu durumda doğrular bir noktada kesişirler. Doğruların kesim noktası çözüm kümesinin elemanıdır.
\[ \;\; \frac{a_1}{a_2} \neq \frac{b_1}{b_2} \Rightarrow d_1 \cap d_2 = P(x_0, \; y_0) \]
Denklem Sisteminin Çözüm Yöntemleri:
a) \[a_1 x+b_1y+c_1=0 \]
\[a_2 x+b_2y+c_2=0 \]
denklem sisteminde bilinmeyenlerden birinin, örneğin \(x\) in katsayıları aynı yapılır. Daha sonra bu iki denklem taraf tarafa çıkarılır. Böylelikle \(y \) bulunmuş olur. Bu \(y \) değeri denklemlerin herhangi birinde yerine yazılarak \( x\) bulunur.
Örnek:
\[
\begin{aligned}
2x + 3x = 8 \\
x + y = 3
\end{aligned}
\]
denklem sisteminin çözüm kümesini bulalim. Denklem sisteminde ikinci denklemin iki yanını 2 ile çarparak taraf tarafa çıkaralım.
\[
\begin{aligned}
2x + 3x &= 8\\
– \quad \quad 2x +2 y &= 6\\
\hline
y &=2
\end{aligned}
\]
elde edilir. \(y = 2 \) değeri ikinci denklemde (veya birinci denklemde) yerine yazılırsa,
\[ x +2 = 3 \Rightarrow x= 1 \] bulunur. O halde, \[ Ç=\{(1,2)\} \] dir.
b)
\[
\begin{aligned}
a_1x + b_1y+ c_1=0
a_2x + b_2y+ c_2=0
\end{aligned}
\]
denklem sisteminde birinci (veya ikinci) denklemden bilinmeyenlerden biri, örneğin \(y, x \) cinsinden bulunur. Bu ifade diğer denklemde yerine yazılır. Böylelikle elde edilen bir bilinmeyenli denklem çözülür. Bulunan \(x \) değeri denklemlerden herhangi birinde yerine yazılarak \(y\) bulunur.
Örnek:
\[
\begin{aligned}
y-3x=2 \\
x + 3y = 16\\
\end{aligned}
\]
denklem sisteminin çözüm kümesini bulalım. Denklem sisteminde birinci denklemden \( y = 3x + 2 \) elde edilerek ikinci denklemde yerine yazılırsa,
\[
\begin{aligned}
x +3 (3x+2) =16 \Rightarrow 10x + 6 = 16\\
\Rightarrow x =1
\end{aligned}
\]
\(x = 1 \) değeri ikinci denklemde yerine yazılırsa,
\[1+ 3y = 16 \Rightarrow y= 5 \] bulunur. O halde, \[ Ç= \{(1,5)\} \] tir.
Soru 14
\[
\begin{aligned}
\frac{1}{x} \;- \;\frac{2}{y} &= 3\\
\\
\frac{2}{x} \;+ \; \frac{1}{y} &= 7\\
\end{aligned}
\]
denklem sistemini sağlayan x değeri kaçtır?
\[
\text{A) } 1 \quad
\text{B) } \frac{5}{3} \quad
\text{C) } \frac{3}{5} \quad
\text{D) } \frac{17}{5} \quad
\text{E) } \frac{5}{17}
\]
Çözüm:
Denklem sisteminde ikinci denklemin her iki yanını 2 ile çarparak taraf tarafa toplayalım.
\[
\begin{aligned}
\frac{1}{x}\; -\; \frac{2}{y} \;=\; &3\\
\\
+ \quad \frac{4}{x}\; +\; \frac{2}{y} = &14\\
\hline
\\
\frac{5}{x} =17
\end{aligned}
\]
\[ \frac{5}{x} = 17 \Rightarrow 5 = 17 x \Rightarrow x = \frac{5}{17}
\]
\(\textbf{Cevab: E} \)
Soru 15
\[
\begin{aligned}
\frac{x+y}{3} -x = 2\\
\\
\frac{x+y}{2} -y = 1\\
\end{aligned}
\]
denklem sistemini sağlayan x değeri kaçtır?
\[
\text{A) } -10 \quad
\text{B) } -9 \quad
\text{C) } -8 \quad
\text{D) } 7 \quad
\text{E) } 6
\]
Çözüm:
Her iki denklemi taraf tarafa toplayalım.
\[
\begin{aligned}
\frac{x+y}{3}\; -\; x \;=\; &2\\
\\
+ \quad \frac{x+y}{2}\; -\; y = \;&1\\
\hline
\\
\frac{5(x+y)}{6}\; – \;(x+y)\;=\;3
\end{aligned}
\]
\[\Rightarrow x+y= -18 \]
bu değer birinci denklemde yerine yazılırsa
\[ -\frac{18}{3} \;- \;x =\; 2 \Rightarrow x \;=\; -8\]
\(\textbf{Cevab: C} \)
Soru 16
\[
\begin{aligned}
\frac{1}{x}\; -y \; &= -1\\
\\
x\; -\; \frac{1}{y} & = \;2\\
\end{aligned}
\]
ise \( \Large \frac{x^2+y^2}{xy} \) kesrinin değeri kaçtır?
\[
\text{A) } 2 \quad
\text{B) } \frac{5}{2} \quad
\text{C) } 3 \quad
\text{D) } \frac{7}{2} \quad
\text{E) } 4
\]
Çözüm:
\[ \frac{1}{x} -y = -1 \Rightarrow \frac{1-xy}{x}= -1 \Rightarrow 1 -xy = -x \]
\[ x \;- \;\frac{1}{y} = 2 \Rightarrow \frac{xy-1}{y}= 2 \Rightarrow 1 -xy = -2y \]
Buaradan,
\[ 1- xy = -x = -2y \]
\[ \Rightarrow x= 2y \]
O halde,
\[\frac{x^2+y^2}{xy} = \frac{(2y)^2 + y^2 }{(2y) \cdot y} = \frac{5}{2} \]
\(\textbf{Cevab: B} \)
Soru 17
\[
\begin{aligned}
\sqrt{ x}\; -\; \frac{1}{\sqrt{y } } & = \frac{3 \sqrt{ 2} }{2} \\
\\
x\; -\; \frac{1}{y} & = \;\frac{15}{2} \\
\end{aligned}
\]
ise x kaçtır?
\[
\text{A) } 4 \quad
\text{B) } 5 \quad
\text{C) } 6 \quad
\text{D) } 7 \quad
\text{E) } 8
\]
Çözüm:
\[
x \;- \; \frac{1}{y} = \frac{15}{2} \Rightarrow
\left( \sqrt{x} \;-\; \frac{1}{\sqrt{y}} \right) \cdot
\left( \sqrt{x} \;+\; \frac{1}{\sqrt{y}} \right) = \frac{15}{2}
\]
\[ \Rightarrow \frac{3 \sqrt{2 } }{2} \cdot \left( \sqrt{x}\; + \; \frac{1}{\sqrt{y}} \right) = \frac{15}{2} \]
\[\Rightarrow \left( \sqrt{x} + \frac{1}{\sqrt{y}} \right) = \frac{5 \sqrt{ 2} }{2} \]
bulunur, Buna göre
\[
\begin{aligned}
\sqrt{x} \;- \;\frac{1}{\sqrt{y}}& = \frac{3\sqrt{2}}{2}\\
\\
+\quad \sqrt{x}\; + \;\frac{1}{\sqrt{y}} &= \frac{5\sqrt{2}}{2}\\
\hline
\\
2\sqrt{x}\; &= \;4\sqrt{2}
\end{aligned}
\]
\[\Rightarrow x = 8 \]
\(\textbf{Cevab: E} \)
Soru 18
\[
\begin{aligned}
2a^2-ab-b^2&=14\\
2a+b&=7\\
\end{aligned}
\]
ise a kaçtır?
\[
\text{A) } 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[ 2a^2-ab-b^2=14 \Rightarrow (2a+b) \cdot (a-b) = 14\]
\[\Rightarrow 7 \cdot (a-b) = 14 \]
\[\Rightarrow (a-b) = 2 \] Bulunur. O halde
\[
\begin{aligned}
2a+ b &=7\\
+ \quad a-b&=2\\
\hline
3a & = 9 \Rightarrow a = 3 \quad \text{bulunur }
\end{aligned}
\]
\(\textbf{Cevab: C} \)
Soru 19
\[
\begin{aligned}
x= \frac{a^2}{2a^2+ 3b^2} \\
y= \frac{b^2}{2a^2+3b^2} \\
\end{aligned}
\]
ise y nin x cinsinden eşiti aşağıdakilerden hangisidir?
\[
\text{A) } -x \quad
\text{B) } 2x-1 \quad
\text{C) } \frac{1-2x}{3} \quad
\text{D) } 1-2x \quad
\text{E) } \frac{x}{3}
\]
Çözüm:
\[ x = \frac{a^2}{2a^2+ 3b^2} \Rightarrow 2x = \frac{2a^2}{2a^2+3b^2} \]
\[ y = \frac{b^2}{2a^2+ 3b^2} \Rightarrow 3y = \frac{3b^2}{2a^2+3b^2} \]
\[
\begin{aligned}
2x= \frac{2a^2}{2a^2+ 3b^2} \\
+ \quad \quad 3y= \frac{3b^2}{2a^2+3b^2} \\\hline \\ \quad
2x+3y= \frac{2a^2+ 3b^2}{2a^2+ 3b^2} = 1\\ \quad
\end{aligned}
\]
\[ y = \frac{1-2x}{3} \]
\(\textbf{Cevab: C} \)
Soru 20
\[ x^2 \cdot y = a – \frac{1}{b}\]
ve
\[ xy^2 = \frac{8b}{1-ab} \]
ise \( x \cdot y \) çarpımı kaçtır?
\[
\text{A) } -2 \quad
\text{B) } 2 \quad
\text{C) } -3 \quad
\text{D) } 3 \quad
\text{E) } 1
\]
Çözüm:
\[ x^2 \cdot y = a – \frac{1}{b} \Rightarrow x^2y= \frac{ab-1}{b} \]
\[ xy^2 = a – \frac{8b}{1-ab} \Rightarrow xy^2= \frac{-8b}{ab-1} \]
\[
\begin{aligned}
x^2y= \frac{ab-1}{b}\\
\times \quad xy^2 = \frac{-8b}{ab-1} \\\hline \\
x^3 y^3= -8 \Rightarrow xy = -2
\end{aligned}
\]
\(\textbf{Cevab: A} \)
← Önceki Sayfa | Sonraki Sayfa →