Hareket Problemleri
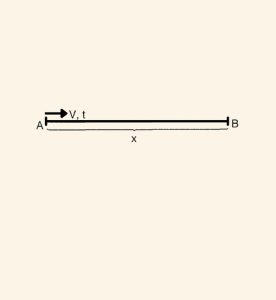
Bir aracın, V ortalama hızıyla, t sürede aldığı \( |AB| \) yolu,
\[ \text{ Yol} = \text{Hız} \times \text{Zaman} \]
\[ |AB| = x = V \times t \] dir.
a) Yetişme Problemi:
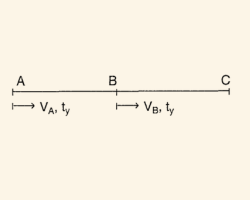
Şekildeki gibi, A ve B noktalarından ortalama hızları \(V_A \) ve \(V_B \) olan iki hareketli aynı anda, aynı yöne doğru hareket ettiklerinde, \( V_A > V_B \) olmak şartıyla, A dan hareket eden hareketli, B den hareket eden hareketliye C noktasında yetişiyor olsun. İki hareketli de C noktasına ayni sürede \( t_y\) varacaklarına göre, A ve B den hareket eden iki hareketlinin aldığı yol sırasıyla,
\(|AC| = V_A \cdot t_y \) ve \(|BC| = V_B \cdot t_y \) iki hareketlinin harekete başladıkları andaki aralarındaki uzaklık ise
\[|AB| = |AC| – |BC| \] dir. Buradan
\[ |AB| =V_A \cdot t_y – V_B \cdot t_y \Rightarrow |AB | = t_y(V_A – V_B) \]
\[t_y= \frac{|AB|}{V_A – V_B} \] elde edilir. O halde
\[ \text{yetişme süresi} = \frac{\text{İki hareketlinin, hareket ettikleri noktalar arasındaki uzaklık} }{\text{iki hareketlinin hızları farkı} }\]
Uyarı:
Burada \(t_y= 1 \) saat alındığında \( |AB | = V_A- V_B \) olur. Buradan, arkadaki hareketli her 1 saatte, aradaki mesafeyi, hızlar farki kadar kapatır, sonucu çıkarılabilir.
Örnek:
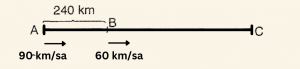
Hızları şekildeki gibi verilen, A ve B noktalarından aynı anda hareket eden A ve B araçlarının hareketini inceleyelim.
1. A aracı, aradaki mesafeyi \[ \frac{240}{90-60} = 8 \; \text{saate kapatır. } \]
2. B aracı 8 saatte \(8 \cdot 60 = 480 \; km \) yol alır. Yani \(|BC| = 480\; km \) dir.
3. A aracı 8 saatte, \(8 \cdot 90 = 720 \; km \) yol alır. Yani \(|AC| = 720\; km \) dir.
b) Karşılaşma Problemi:
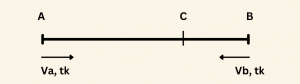
Şekildeki gibi, A ve B noktalarından, ortalama hızları \( V_a\) ve \( V_b \) olan iki hareketli, aynı anda, birbirlerine doğru (zıt yönde), hareket ettiklerinde, C noktasında karşılaşıyor olsun. İki hareketli de C noktasında aynı sürede \( (t_k) \) varacaklarına göre, A ve B den hareket eden iki hareketlinin aldığı yol sırasıyla,
\[ |AC| = V_a \cdot t_k \]
\[ |BC| = V_b \cdot t_k \]
şeklinde yazılır. İki hareketlinin, harekete başladıkları andaki aralarındaki uzaklık ise
\[ |AB| = |AC| + |BC| \; \text{dir} \] Buradan
\[ |AB| = V_A \cdot t_k + V_B \cdot t_k \Rightarrow |AB| = t_k(V_A + V_B)\]
\[t_k = \frac{|AB|}{V_A+ V_B} \] elde edilir. O halde
\[ \text{karşılaşma süresi} = \frac{\text{İki hareketlinin, hareket ettikleri noktalar arasındaki uzaklık} }{\text{iki hareketlinin hızları toplamı} }\]
Uyarı:
Burada \(t_k= 1 \) saat alındığında \( |AB | = V_A + V_B \) olur. Buradan, iki hareketli, her 1 saatte, hızlar toplamı kadar birbirine yaklaşır, sonucu çıkarılabilir.
Örnek:
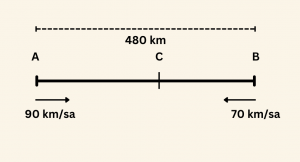
Hızları şekildeki gibi verilen, A ve B noktalarından aynı anda hareket eden A ve B araçlarının hareketini inceleyelim.
1) iki araç arasındaki mesafe, \[\frac{480}{90 + 70 } = 3 \; \text{saat } \] sonra kapanır. İki araç 3 saat sonra karşılaşır.
2) 3 saatte A aracı \( 3 \cdot 90 = 270 \) km yol alır. Yani IACI = 270 km dir.
3) 3 saatte B aracı \( 3 \cdot 70 = 210 \) km yol alır. Yani IBCI = 270 km dir.
b) Ortalama Hız:
Ortalama hız, bir hareketlinin, bir yolu, belli zaman aralıklarında farklı sabit hızlarla katettiğinde söz konusu olur. Ancak, aracın bu yol boyunca, belli aralıklarda değişen hızlarının aritmetik ortalaması şeklinde düşünülmemelidir.
Bir aracın iki nokta arasında katettiği toplam yolun, bu mesafeyi tamamladığı toplam zamana oranı (bölümü), aracın bu iki nokta arasındaki ortalama hızıdır.
Buna göre,
\[ V_{ort} = \frac{\text{toplam yol} }{\text{toplam zaman} } \]
şeklinde hesaplanır.
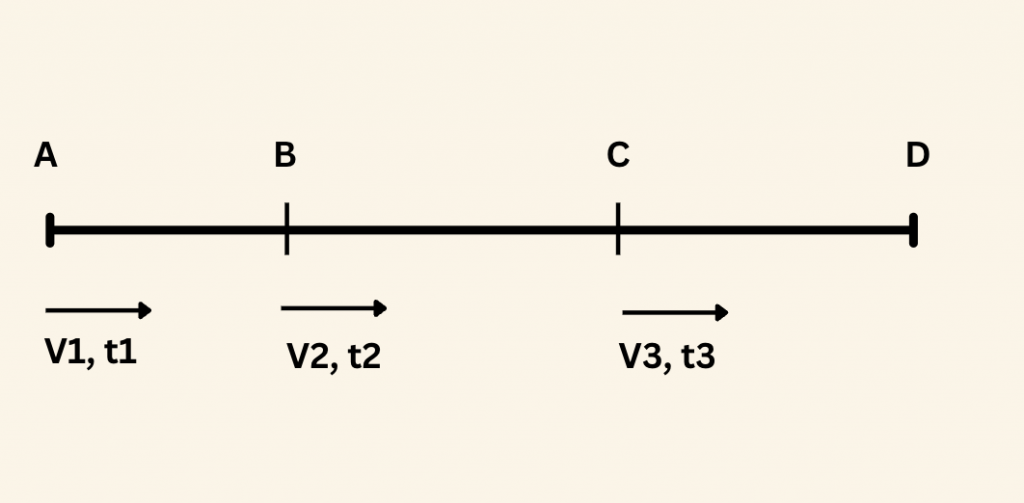
Yukarıdaki şekilde gösterilen, A dan hareket eden bir araç, AB yolunu, \(V_1 \) hızıyla \(t_1 \) sürede, BC yolunu \(V_2 \) hızıyla, \(t_2 \) sürede, CD yolunu \(V_3 \) hızıyla \(t_3 \) sürede almış olsun. Bu aracın AD yolu boyunca, ortalama hızı,
\[ V_{ort} = \frac{|AD|}{t_1 +t_2 + t_3} \] veya \[ V_{ort} = \frac{|AD|}{\frac{|AB|}{V_1} + \frac{|BC|}{V_2} + \frac{|CD|}{V_3} } \] olur.
Örnek:
Bir araç, gideceği yolun üçte birini 60 km/sa, geriye kalanını 80 km/sa hızla katettiğine göre bu aracın katettiği bu yoldaki ortalama hızını bulalım.
Bu aracın hareketini gösteren şekil aşağıdaki gibi çizilirse,
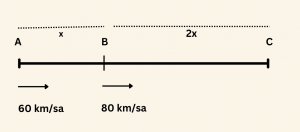
Aracın katettiği toplam yol \(3x \) km olmak üzere,
\[ V_{ort} = \frac{\text{toplam yol} }{\text{toplam zaman}} = \frac{3x}{\frac{x}{60} + \frac{2x}{80} } = \frac{3x}{ x \cdot \left( \frac{1}{60} + \frac{1}{40} \right)} \]
\[ V_{ort} = 72 \; \text{km/sa bulunur} \]
Soru 16
Hızları 50 km/sa ve 90 km/sa olan iki araç A sehrinden B sehrine gidiyorlar. Hızı fazla olan araç diğerinden 4 saat sonra yola çıkıp, 2 saat önce B sehrine varıyor.
Buna göre A ve B şehirleri arası kaç kilometredir?
\[
\text{A )} 550 \quad
\text{B) } 600 \quad
\text{C) } 675 \quad
\text{D) } 725 \quad
\text{E) } 750
\]
Çözüm:
Hızı 90 km/sa olan araç IABI mesafesini \( t\) saatte almış olsun. Bu durumda, hızı 50 km/sa olan araç iki şehir arasındaki yolu \( t+ 6\) saatte kateder.
Buna göre verilen probleme ait denklem
\[ |AB | = 90 \cdot t = 50 \cdot (t+6 )\] şeklinde yazılırsa, \[ = 40 \cdot t = 300 \Rightarrow t = \frac{15}{2} \; \text{saat bulunur} \]
\[|AB| = 90 \cdot t \Rightarrow |AB | = 90 \cdot \frac{15}{2} = 675 \; \text{km dir.} \]
\(\textbf{Cevab: C} \)
Soru 17
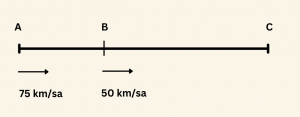
A ve B den aynı anda ve aynı yönde hareket eden iki aracın saatteki hızları sırasıyla 75 km ve 50 km dir. A dan hareket eden araç harekete başladıktan 2 saat sonra mola veriyor. 1 saatlik moladan sonra aynı hızla yoluna devam edip öndeki araca C noktasında yetişiyor. AB yolu 75 km olduğuna göre BC yolu kaç km dir?
Buna göre A ve B şehirleri arası kaç kilometredir?
\[
\text{A )} 300 \quad
\text{B) } 250 \quad
\text{C) } 200 \quad
\text{D) } 150 \quad
\text{E) } 100
\]
Çözüm:
AB yolu 75 km olduğuna göre, A dan hareket eden araç B den hareket eden araca
\[ \frac{75}{75-50} = 3 \] saat sonra yetişebilirdi.
A dan hareket eden araç öndeki araca yetişmeden 1 saat mola verdiği için B den hareket eden araç, bu 1 saatte aradaki mesafeyi \(50 \cdot 1 = 50 \) km daha açmıştır. Buna göre A dan hareket eden aracın, öndeki araç ile kapatması gereken toplam mesafe \( 75 + 50 = 125\) km dir. O halde bu 125 km yi
\[\frac{125}{75-50} = 5 \] saatte kapatacaktır. Ayrıca A dan hareket eden aracın verdiği 1 saatlik mola sırasında B den hareket eden araç \( 50 \cdot 1 = 50\) km yol almıştır. Buna göre, B den hareket eden aracın aldığı toplam yol
\[ |BC| = 50 \cdot 5 + 50 = 300 \; \text{km dir. } \]
\(\textbf{Cevab: A} \)
Soru 18
Bir koşucunun hızının rüzgar hızına oranı \(\Large \frac{5}{2} \) dir. Bu koşucu 45 km lik bir mesafeyi, rüzgara karşi 5 saatte koşabildiğine göre, koşucunun saatteki hızı kaç km dir?
\[
\text{A )} 3 \quad
\text{B) } 9 \quad
\text{C) } 12 \quad
\text{D) } 15 \quad
\text{E) } 18
\]
Çözüm:
Rüzgarın hızına \( 2v \) denilirse koşucunun hızı \( 5v \) olur. Koşucu rüzgara karşı koştuğu zaman, hızı \[ 5v \;- \; 2v = 3v \] olduğundan verilen probleme ait eşitlik:
\[ \text{ Yol = Hiz x Zaman } \] olduğundan, \[ 45 = 3v. 5 \Rightarrow v= 3 \; km/saat \]
koşucunun hızı ise \( 5V = 15 \) km/saat tir.
\(\textbf{Cevab: D} \)
Soru 19
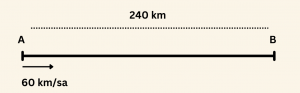
A noktasından 60 km/saat hızla hareket eden bir otobüs, hareket ettikten 1 saat sonra hızını V kadar arttırınca B noktasına varması gereken zamandan 1 saat önce ulaşıyor. AB yolu 240 km olduğuna göre, V kaç km/saat tir?
\[
\text{A )} 20 \quad
\text{B) } 25 \quad
\text{C) } 30 \quad
\text{D) } 35 \quad
\text{E) } 40
\]
Çözüm:
Otobüs harekete başladıktan 1 saat sonra \( 60 \cdot 1 = 60 \) km ilerlemiştir. Geriye gitmesi gereken \( 240 \; – \; 60 = 180 \) km yolu kalmıştır. Hızını değiştirmezse, bu yolu \[ \frac{180}{60} = 3 \text{ saat} \] sonra tamamlayacaktır. Ancak hızını \(V\) kadar artırdığında, B’ye varması gereken zamandan 1 saat önce ulaştığına göre, 180 km mesafeyi 2 saatte tamamlamıştır. Buna göre: \[ (60 + V) \cdot 2 = 180 \] eşitliği yazılır ve çözülür: \[ 60 + V = \frac{180}{2} = 90 \] \[ V = 90 \; – \; 60 = 30 \, \text{km/saat} \] Sonuç olarak, hız artışı \(V = 30\) km/saat bulunur.
\(\textbf{Cevab: C} \)
Soru 20
Bir araç saatte 80 km hızla gittiği bir AB yolunu, dönüşte saatte 60 km hız yaparak katediyor. Gidiş – dönüş süresi toplam 14 saat olduğuna göre, AB yolu kaç km dir?
\[
\text{A) } 480 \quad
\text{B) } 460 \quad
\text{C) } 420 \quad
\text{D) } 300 \quad
\text{E) } 350
\]
Çözüm:
Aracın gidiş süresine t denilirse, dönüş süresi \(14 – t \) olur. Araç gidişte 80 km/saat, dönüşte 60 km/saat hız yaptığına göre verilen probleme ait denklem
\[ |AB| = 80 \cdot t = 60 \cdot (14 \; – \; t )\] şeklinde yazılırsa
\[ 14t = 6 \cdot 14\]
\[\Rightarrow t = 6 \; \text{saat olarak bulunur.} \]
Buradan,
\[ |AB| = 80 \cdot t \; \text{olduğundan } \]
\[ |AB| = 80 \cdot 6 = 480 \; \text{km dir } \]
\(\textbf{Cevab: A} \)
Soru 21
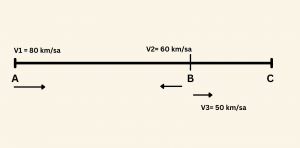
\( V_1 = 80 \) km/saat, \( V_2 = 60 \) km/saat, \( V_3 = 50 \) km/saat olmak üzere, üç araç aynı anda A ve B noktasından şekilde gösterilen yönlerde hareket ediyorlar. \( V_1 \) hızıyla hareket eden araç \( V_2 \) hızıyla hareket eden araçla 3 saat sonra karşılaşıyor ve \( V_3 \) hızıyla hareket eden araca C noktasında yetişiyor. Buna göre BC mesafesi kaç km dir?
\[
\text{A) } 420 \quad
\text{B) } 480 \quad
\text{C) } 540 \quad
\text{D) } 680 \quad
\text{E) } 700
\]
Çözüm:
\( V_1 \) ve \( V_2 \) hızıyla birbirlerine doğru hareket eden iki araç 3 saat sonra karşılaştığına göre AB mesafesi
\[ |AB| = 3 \cdot (V_1 + V_2) \Rightarrow |AB| = 3 \cdot (80 + 60 ) = 420 \: \text{km dir.} \] \( V_1 \) hızlı araç \( V_3 \) hızlı araca t saatte yetişirse,
\[ t = \frac{|AB|}{V_1 \;- \; V_3} \Rightarrow t = \frac{420}{80 \;-\; 50 } = 14 \; \text{saat olur. } \]
V3 hızıyla hareket eden araç 14 saatte B den C ye vardığına göre,
\[ |BC| = 50 \cdot 14 \Rightarrow |BC| = 700 \; \text{km dir.} \]
\(\textbf{Cevab: E} \)
← Önceki Sayfa | Sonraki Sayfa →