Kâr – Zarar Hesapları
b) Kâr – Zarar Hesapları:
Alınan bir mal için ödenen bedele alış fiyatı denir. Bazen alınan malların satış yerine getirilmesi için bir takım masraflar daha yapılır. Yapılan bu masraflar da alış fiyatına eklenir. Alış fiyatına, bu mal için yapılan masrafların da eklenmesiyle elde edilen fiyata maliyet fiyatı denir.
Buna göre:
\[ \text{Maliyet Fiyatı} = \text{Alış Fiyatı} + \text{Masraflar} \]
Eğer masraf yapılmamışsa alış fiyatı maliyet fiyatına eşit olur. Maliyet fiyatına, kâr eklenmesiyle meydana gelen fiyata satış fiyatı veya etiket fiyatı denir.
Buna göre:
\[ \text{Satış (Etiket) Fiyatı} = \text{Maliyet Fiyatı} + \text{Kâr} \]
Bazen çeşitli sebeplerle, alınan mal, maliyet fiyatından daha düşük fiyata, zararına satılır. Bu durumda:
\[ \text{Satış Fiyatı} = \text{Maliyet Fiyatı}\; -\; \text{Zarar} \]
şeklinde olur.
Örnek:
Bir manav, elindeki limonların tanesini 2 liradan satacak olursa 15 lira kâr, 1,200 liradan satacak olursa 9 lira zarar edecektir. Buna göre, manavın elinde kaç tane limon olduğunu bulalım.
Manavın elindeki x tane limonun maliyeti a lira olsun.
\[ \text{Satış (Etiket) Fiyatı} = \text{Maliyet Fiyatı} + \text{Kâr} \]
\[2000 \cdot x = a + 15000 \]
\[ \text{Satış Fiyatı} = \text{Maliyet Fiyatı}\; -\; \text{Zarar} \]
\[ 1200 \cdot x = a -9000 \]
İki denklemi alt alta yazarsak
\[
\begin{aligned}
&2 \cdot x = a +15 \\
– \quad &1,2 \cdot x = a -9
\\
\hline \\ 0, 8 \cdot &x = 24 \Rightarrow x = 30 \; \text{bulunur. }
\end{aligned}\]
Soru 22
Bir kırtasiyeci elindeki kalemlerin üçte birini tanesi 3 liradan, geriye kalanların tanesini 5 liradan satın almıştır. Bu kırtasiyeci kalemlerin tanesini 6 liradan satarak 100 lira kâr ettiğine göre, kırtasiyecinin elindeki kalemlerin sayısı kaçtır?
\[
\text{A) } 40 \quad
\text{B) } 50 \quad
\text{C) } 60 \quad
\text{D) } 70 \quad
\text{E) } 80
\]
Çözüm:
\( \Rightarrow \) Kırtasiyecinin elindeki kalemlerin sayısına \(3x\) denilirse:
\( \Rightarrow \) Kalemlerin üçte birinin alış fiyatı: \(x \cdot 3 \; \text{TL} \)
\( \Rightarrow \) Kalemlerin geriye kalanının alış fiyatı: \(2x \cdot 5 \; \text{TL} \)
\( \Rightarrow \) Kalemlerin satış fiyatı: \(3x \cdot 6 \; \text{TL} \)
Buna göre, verilen probleme ait denklem:
\[ \text{Kâr} = \text{Satış Fiyatı} – \text{Alış Fiyatı} \]
şeklinde yazılır. Veriler yerine konulduğunda:
\[ 100= 3x \cdot 6- (x \cdot 3+ 2x \cdot 5) \]
Denklem çözülür:
\[ 100= 18x – (3x + 10x) \]
\[ 100= 18x – 13x \]
\[ 100= 5x \]
\[ x = \frac{100}{5} = 20 \]
Buradan, kırtasiyecinin elindeki kalemlerin sayısı:
\[ 3x = 3 \cdot 20 = 60 \]
Sonuç olarak, satıcının elindeki kalemlerin sayısı 60’tır.
\(\textbf{Cevab: C} \)
Arttırma:
Bir \( x \) sayısı \( \%a \) arttırılırsa yeni sayı,
\[ x + x \cdot \frac{a}{100} = \frac{(100 + a )}{100} \cdot x \] olur
Örnek:
100 sayısı % 20 arttırılırsa yeni sayı
\[ 100 + 100 \cdot \frac{20}{100} = 120 \] olur.
Örnek:
\( 20\;000 \) liraya alınan bir malın % 30 kârla kaç liraya satılacağını bulalım.
\[ 20\;000 \cdot \frac{30}{100} = 6\;000 \] lira eklenirse, satış fiyatı \( 26\;000 \) lira olur.
Komisyon Hesapları:
Bir malın alım satımına aracılık eden kimseye komisyoncu, bu iş için ödenen paraya da komisyon denir.
Örnek:
Bir emlak komisyoncusu satışına aracılık ettiği her daireden % 1,5 komisyon almaktadır. Buna göre 8 milyon liraya satılan bir daire için alacağı komisyonu bulalım.
\[ 8\;000\;000 \cdot \frac{1,5}{100} = 120\;000\] olduğundan komisyoncunun bu satıştan alacağı komisyon \(120\;000 \) lira olarak bulunur.
İskonto(İndirim):
Bazen satılan mallar, bir takım sebeplerle satış (etiket) fiyatından daha düşük fiyata satılır. Buna indirim (iskonto) denir.
Bir x sayısı %a azaltılırsa yeni sayı,
\[ x -x \cdot \frac{a}{100} = \frac{100-a }{100} \cdot x \] olur.
Örnek:
Bir mağaza, mevsim sonu dolayısı ile satışlarında % 20 indirim uygulamaktadır. Buna göre etiket fiyatı 750 lira olan bir gömlek için yapılacak olan indirim miktarını ve bu gömleğin indirimli satış fiyatını bulalım.
% 20 indirim yapıldığına göre 750 lira için yapılan indirim \(750 \cdot 20 = 150 \) lira, indirimli satış fiyatı ise \( 750 – 150 =600 \) lira olarak bulunur.
Uyarı:
Yüzde problemlerinin çözümünde kolaylık olması bakımından bilinmeyenler için değişkenler seçmek yerine uygun sayı değerleri seçilebilir.
Soru 23
Bir dikdörtgenin kısa kenarı % 50 arttırılıp uzun kenarı % 20 azaltılırsa, dikdörtgenin alanındaki değişme ne olur?
\[
\text{A) } % 15\; \text{Artar} \quad
\text{B) } % 15\; \text{Azalır} \quad
\text{C) } % 20\; \text{Artar} \quad
\text{D) } % 20\; \text{Azalır} \quad
\text{E) } % 25\; \text{Artar}
\]
Çözüm:
Kare özel bir dikdörtgen olduğundan, problemin çözümü için alanı 100 birim kare olan dikdörtgen yerine, alanı 100 birim kare olan kare seçilirse daha kolay çözüm yapılır. Buna göre,
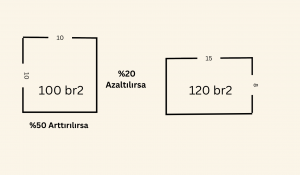
10 birim \( \%\ 50 \) artırılırsa \[ \frac{100+50}{100} \cdot 10 = 15 \; \text{birim} \]
10 birim \( \% 20 \) azaltılırsa \[ \frac{100-20}{100} \cdot 10 = 8 \; \text{birim olur. } \]
Son durumda dikdörtgenin alanı
\[15 \cdot 8 = 120 \; \text{birim kare olur.} \]
Alan 100 birim kare iken 120 birim kare olduğuna göre % 20 artmıştır.
\(\textbf{Cevab: C} \)
Soru 24
Bir satıcı, satışları artırmak maksadıyla fiyatlarda %20 indirim yapıyor. Satışlarının beklediği gibi artmadığını görünce, indirimli fiyat üzerinden %15 daha indirim yapıyor. Buna göre, satıcının yaptığı indirimin toplam miktarı yüzde kaçtır?
\[
\text{A) } 40 \quad
\text{B) } 38 \quad
\text{C) } 35 \quad
\text{D) } 32 \quad
\text{E) } 28
\]
Çözüm:
Satılan malların etiket fiyatı 100 lira olsun. İlk olarak %20 indirim yapıldığında:
\[ 100 \cdot \frac{20}{100} = 20 \, \text{lira indirim yapılır.} \]
Bu durumda, indirilen fiyat: \[ 100 \,-\; 20 = 80 \, \text{liradır.} \]
Daha sonra indirimli fiyat üzerinden %15 indirim yapılır:
\[ 80 \cdot \frac{15}{100} = 12 \, \text{lira indirim yapılır.} \]
Bu durumda, ikinci indirimin ardından fiyat:
\[ 80 \,- \,12 = 68 \, \text{liradır.} \] Toplam indirim miktarı:
\[ 100\, – \, 68 = 32 \, \text{liradır.} \] Toplam indirimin yüzdesi: \[ \frac{32}{100} \cdot 100 =\% 32 \] Sonuç olarak, yapılan toplam indirim \( \% \,32 \) ’dir.
\(\textbf{Cevab: D} \)
Soru 25
Bir satıcı, elindeki malların dörtte birini %30 kâr ile, geriye kalanının üçte ikisini %30 zarar ile satmıştır. Mallarının en son geriye kalan kısmını yüzde kaç kâr ile satmalı ki bu alış veriş sonunda toplam %5 kâr etmiş olsun?
\[
\text{A) } 50 \quad
\text{B) } 45 \quad
\text{C) } 40 \quad
\text{D) } 35 \quad
\text{E) } 25
\]
Çözüm:
Satıcının elindeki malları 4 birim olarak düşünelim.
İlk olarak malların dörtte biri, yani 1 birimi %30 kâr ile satılmıştır. Bu satışın kâr oranı:
\[ 1 \cdot \frac{30}{100} \]
Malların geriye kalan kısmı: \(4 – 1 = 3\) birimdir. Bu kalan kısmın üçte ikisi, yani:
\[ \frac{3 \cdot 2}{3} = 2 \, \text{birim} \] %30 zarar ile satılmıştır. Bu satışın zarar oranı: \[ 2 \cdot \frac{-30}{100} \]
En son kalan 1 birim mal, %\(x\) kâr ile satılacaktır. Bu durumda bu satışın kârı: \[ 1 \cdot \frac{x}{100} \] Satıcının toplam %5 kâr ettiğine göre, bu 4 birimden elde edilen toplam kâr oranı: \[ 4 \cdot \frac{5}{100} \] Buna göre, problemde verilen denklem şu şekilde yazılır: \[ 1 \cdot \frac{30}{100} + 2 \cdot \frac{-30}{100} + 1 \cdot \frac{x}{100} = 4 \cdot \frac{5}{100} \]
Denklem çözülür: \[ \frac{30}{100} – \frac{60}{100} + \frac{x}{100} = \frac{20}{100} \] \[ \frac{-30}{100} + \frac{x}{100} = \frac{20}{100} \]
\[ \frac{x}{100} = \frac{20}{100} + \frac{30}{100} \] \[ \frac{x}{100} = \frac{50}{100} \] \[ x = 50 \]
Sonuç olarak, satıcı en son kalan malı % 50 kâr ile satmalıdır.
\(\textbf{Cevab: A} \)
Soru 26
Bir satıcı % 15 zararla statığı bir maldan 120 bin lira zarar ediyor. Ayni malı % 20 karla satarsa bu malın satış fiyatı kaç bin lira olur?
\[
\text{A) } 800 \quad
\text{B) } 840 \quad
\text{C) } 920 \quad
\text{D) } 960 \quad
\text{E) } 980
\]
Çözüm:
Satılan malın % 20 kârla satış fiyatı x olsun. Bu malın satış fiyatı maliyetinin % 120 sidir. Bu mal % 15 zararla satıldığında 120 bin lira zarar edildiğine göre malın maliyetinin % 15 i 120 bin liradır. O halde orantı kurulursa,
\[
\begin{aligned}
&\% 15 \; i \quad \quad &120\,000 \\
&\%120 \; si \quad \quad &x \;\; \text{liradır. } \\
\\
\hline \text{Doğru Orantı}
\end{aligned}
\]
\[ 15 \cdot x = 120 \cdot 120\;000 \Rightarrow x = 960 \;000\] lira bulunur.
\(\textbf{Cevab: D} \)
Soru 27
Alış fiyatı \(x\), satış fiyatı \(y\) olan bir malın alış fiyatı ile satış fiyatı arasında:
\[ y = 290\,000 – 4x \] bağıntısı vardır. %80 kâr ile satılan bu malın satış fiyatı kaç bin liradır?
\[
\text{A) } 100 \quad
\text{B) } 90 \quad
\text{C) } 80 \quad
\text{D) } 70 \quad
\text{E) } 50
\]
Çözüm:
\(x \) liraya alınan mal % 80 kârla satıldığına göre bu malın satış fiyatı
\[y = \frac{180}{100} \cdot x \] tir. Buna göre verilen probleme ait denklem
\[ y = 290\;000 – 4x = \frac{180}{100}x \] şeklinde yazılırsa \[x = 50 \;000 \] lira bulunur.
O halde bu malın satış fiyatı
\[ y= 290\;000 \; -\; 4 \cdot 50\;000 = 90\; 000 \; \text{lira olur. } \]
\(\textbf{Cevab: B} \)
Soru 28
% 45 kârla satılan bir mal, etiket fiyatı üzerinden % 20 indirim yapılarak satıldığı zaman maliyet fiyatı üzerinden 3200 lira kâr ediliyor. Buna göre bu malın etiket fiyatı kaç liradır?
\[
\text{A) } 30000 \quad
\text{B) } 29000 \quad
\text{C) } 28000 \quad
\text{D) } 27000 \quad
\text{E) } 25000
\]
Çözüm:
Bu malın maliyet fiyatı \(x\) olsun. %45 kârla satılan malın etiket fiyatı:
\[ \frac{145}{100} \cdot x \]
olur. Etiket fiyatı üzerinden %20 indirim yapıldığı zaman, indirimli satış fiyatı:
\[ \left(\frac{145}{100} \cdot x \right) \cdot \frac{80}{100} \]
olur. Bu durumda maliyeti üzerinden \(3\,200\) lira kâr elde edildiğine göre, indirimli satış fiyatı aynı zamanda \(x + 3\,200\) liradır. Buna göre verilen probleme ait denklem şu şekilde yazılır:
\[ \left(\frac{145}{100} \cdot x \right) \cdot \frac{80}{100} = x + 3\,200 \]
Denklem sadeleştirilirse: \[ \frac{145}{100} \cdot \frac{80}{100} \cdot x = x + 3\,200 \]
\[ \frac{145 \cdot 80}{10\,000} \cdot x = x + 3\,200 \]
\[ \frac{11\,600}{10\,000} \cdot x = x + 3\,200 \]
\[ 1.16x = x + 3\,200 \] \[ 1.16x – x = 3\,200 \]
\[ 0.16x = 3\,200 \]
\[ x = \frac{3\,200}{0.16} = 20\,000 \]
Bulunan maliyet fiyatı \(x = 20\,000\) liradır. O hâlde etiket fiyatı şu şekilde hesaplanır:
\[ \frac{145}{100} \cdot 20\,000 = 29\,000 \, \text{lira}. \]
Sonuç olarak etiket fiyatı \(29\,000\) liradır.
\(\textbf{Cevab: B} \)
← Önceki Sayfa | Sonraki Sayfa →