Küme Çeşitleri
Boş Küme
Hiçbir elemanı olmayan kümeye boş küme denir. Boş küme, { } veya Ø şeklinde gösterilir.
Örnek:
\( A = \{x | \;\; x^2 +1 = 0 \;\; x \in R \}\) kümesi
\( \Rightarrow x^2 +1 > 0 \) olduğundan boş kümedir.
\( A = \{\} \) veya \( A= \) Ø, \(s(A)=0 \) dır.
Alt Küme:
A ve B gibi iki kümeden, B kümesinin her elemanı A kümesinin de elemanı ise B kümesi A kümesinin alt kümesidir veya A kümesi B kümesini kapsar denir. \( B \subset A \) veya \( A \supset B \) şeklinde gösterilir.
Burada:
\(\bullet \quad \) \( \subset \;\; \): Alt küme
\(\bullet \quad \) \( \supset \;\; \) : Kapsar işaretidir.
Örnekler:
\(\bullet \quad \)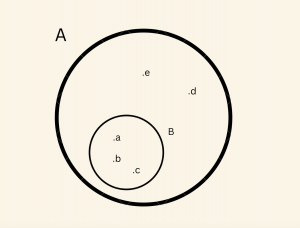
\( A \supset B \)
\(\bullet \quad \) \( F = \{ a, b, c \} \) kümesinin alt kümeleri
\( F = \{ a, b, c \} , \{ a, b\} ,\{a, c \} ,\{b,c \}, \{a\}, \{b\}, \{b\}, \{ \} \) olmak üzere 8 tanedir.
Uyarı:
\(\bullet \quad \) Her küme kendisinin alt kümesidir. \( A \subset \;\; A \)
\(\bullet \quad \) Boş küme her kümenin alt kümesidir. \( Ø \subset \;\; A\)
Alt Küme Sayisi:
n elemanli bir kümenin alt kümelerinin sayısı,
\[ 2^n \;\; \text{dir.} \]
Soru 1
\(A= \{ a, \{ a\} , Ø , b, c, \{b, d \} \} \) kümesinin kaç tane alt kümesi vardır?
\[
\text{A)} 8 \quad
\text{B) } 16 \quad
\text{C) } 32\quad
\text{D) } 64 \quad
\text{E) } 128
\]
Çözüm:
\( s(A) = 6 \) olduğuna göre, A kümesinin \(2^6= 64 \) tane alt kümesi vardır.
\(\textbf{Cevab: D} \)
Soru 2
\(A= \{ a, b, c , d, e , f \} \) kümesinin kaç tanesinde a elemanı bulunur, b elamanı bulunmaz ?
\[
\text{A)} 32 \quad
\text{B) } 16 \quad
\text{C) } 8\quad
\text{D) } 4 \quad
\text{E) } 2
\]
Çözüm:
Alt kümelerde b elemanı bulunmayıp a elemanı bulunacağına göre, { c, d, e, f} kümesinin elemanları ile \(2^4= 16 \) tane alt küme yazılıp, bu alt kümelerin her birine a elemanı eklenecektir. O halde istenen şartlarda 16 tane alt küme yazılabilir.
\(\textbf{Cevab: B} \)
Öz Altküme
Bir kümenin kendisinden farklı alt kümelerine bu kümenin özalt kümeleri denir.
Örnek:
\( A = \{ 1, 2 , 3 \} \) kümesinin özalt kümeleri:
\[ A= \{ 1, 2 \} , \{1,3 \} , \{ 2, 3 \} , \{1 \} , \{ 2\} , \{ 3\} , \{ \} \] olmak üzere 7 tanedir.
n elemanlı bir kümenin özalt Kümelerinin sayısı
\[ 2^n-1 \;\; \text{dir. } \]
Soru 3
Alt kümelerinin ve özalt kümelerinin sayıları toplamı 63 olan bir kümenin eleman sayısı kaçtır ?
\[
\text{A)} 3 \quad
\text{B) } 4 \quad
\text{C) } 5\quad
\text{D) } 6 \quad
\text{E) } 7
\]
Çözüm:
Bu kümenin eleman sayısı n olsun.
\[ 2^n + 2^n-1 = 63 \Rightarrow 2 \cdot 2^n = 64 \]
\[ \Rightarrow 2^n = 32 = 2^5 \Rightarrow n= 5 \]
\(\textbf{Cevab: C} \)
Evrensel Küme
Üzerinde işlem yapılan tüm kümeleri kapsayan kümeye evrensel küme denir. Evrensel küme E sembolüyle gösterilir.
Örnek:
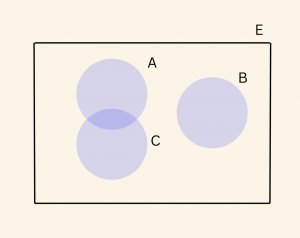
Bir Kümenin Tümleyeni
Bir \( A \) kümesi, \( E \) evrensel kümesinin alt kümesi olsun. \( E \) de olup da \( A \) da olmayan elemanların kümesine \( A \) kümesinin tümleyeni denir ve \( A’ \) veya \( \overline{A} \) şeklinde gösterilir.
\[ \overline{A} = A’ = \{ x \, | \, x \in E \text{ ve } x \notin A \} \]
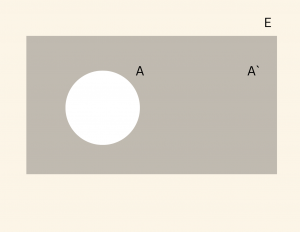
Özellikler:
\(1.)\;\; E’= Ø \quad \quad 2.) \;\; Ø’ = E \quad \quad 3.) \;\; (A’)’ = A \)
\(4.)\;\; B \subset A \;\; \text{ise } B’ \supset A’ \quad \quad 5.) \;\; s(A) + s(A’) = s(E)\)
Örnek:
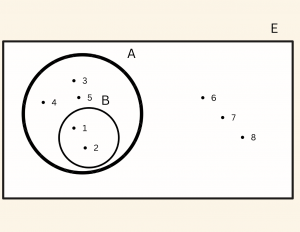
\[\begin{aligned} A’= \{ 6,7,8 \} \\ B’= \{3,4,5,6,7,8 \} \\ B\subset A \;\; \text{ve } \;\; B’\; \supset\; A’ \end{aligned}\]
Örnek:
\( E= R \) ve \( A = \{ x \; | \; x< 0 \;\; \text{veya } \; x ≥ 3 , \; x \in R \} \) ise \( A’ \) kümesini bulalım?
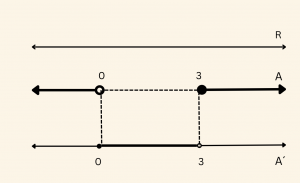
\[ A’ = \{x \;| \; 0 ≤ x < 3 , x \in R \} \]
← Önceki Sayfa | Sonraki Sayfa →