Kartezyen Çarpım
\( A\) ve \( B \) boş olmayan iki küme olmak üzere, birinci bileşeni \( A\) dan, ikinci bileşeni \( B \) den alınarak meydana getirilen tüm sıralı ikililerin kümesine \( A\) ile \( B \) nin kartezyen çarpımı denir. \( A \times B \) şeklinde gösterilir ve \( A\) kartezyen çarpım \( B \) diye okunur. Buna göre,
\[ A \times B = \{ (x,y ) \;| \; x \in A \quad \text{ve } \quad y \in B \} \] dir.
Tanım: İki kümenin Kartezyen çarpımı, birinci kümeden bir eleman ile ikinci kümeden bir elemanın oluşturduğu sıralı ikililer kümesidir.
Örnek:
Aşağıdaki kümeleri ele alalım:
Bu durumda, \( A \times B \) şu sıralı ikililerden oluşur:
\[ A \times B = \{ (1, a ), (1,b ), (2,a ), (2, b )\} \]
Bu sıralı ikililer, Kartezyen koordinat sisteminde noktalar olarak temsil edilebilir.
2. Matematiksel Sembollerin Anlamları
\( \bullet \) Sıralı İkili ( x, y ) : Birinci elemanı \(x \), ikinci elamanı \(y \) olan çiftleri ifade eder. Bu gösterim, özellikle Kartezyen çarpımında ve koordinat sistemlerinde kullanılır.
\( \bullet \) Küme Parantezleri ( { } ) : Bir kümenin elemanlarını belirtmek için kullanılır. Örneğin {1, 2, 3 } kümesi 1, 2 ve 3 elemanlarını içerir.
\( \bullet \) Dikey Çizgi ( | ) : Küme tanımlarında “öyle ki” anlamında kullanılır. Örneğin \( { x \; | \; x > 0 } \) ifadesi “x öyle ki x pozitiftir” anlamına gelir.
Not: Kartezyen çarpımın tanımında, sıralı ikililerin her iki bileşeninin de ilgili kümelerin elemanları olması gerektiğinden, “ve” yada matematiksel mantık işareti “\( \land \) ” bağlacı kullanılır.
Örnek:
\( A= \{1, 2, 3 \} \) ve \( B= \{a, b \} \) ise,
\[ A \times B = \{ (1, a ), (1, b), (2, a), (2, b), (3, a ), (3, b )\} \]
\[ B \times A = \{ (a, 1 ), (a, 2 ), (a, 3), (b, 1), (b, 2 ), (b, 3 \} \]
Uyarı:
\[ A \times A = \{ (x,y ) \;| \; x \in A \quad \text{ve } \quad y \in A \} \] dır.
\( A= \{1, 2 \} \) ise
\[ A \times A = \{ (1,1 ), (1,2 ), (2,1 ), (2,2 ) \} \]
Uyarı:
\[ A \times B \times C = \{ (x,y, z ) \;| \; x \in A \quad \text{ve } \quad y \in B \quad \text{ve } \quad z \in C \} \] dir.
\( A= \{1, 2 \}, \quad B =\{ a, b \}, \quad C = \{n\} \) ise
\[ A \times B \times C = \{ (1,a, n ), (1,b,n ), (2,a,n ), (2,b,n ) \}\quad\] dir.
Kartezyen Çarpımın Özellikleri:
\( 1) \quad \) Kartezyen çarpımın değişme özelliği yoktur.
\[ A \times B ≠ B \times A \quad (A \neq B)\]
\( 2) \quad \) Kartezyen çarpımın birleşme özelliği vardır.
\[A \times B \times C = A \times (B \times C ) = (A \times B) \times C \]
\( 3) \quad \) Kartezyen çarpımın kümelerdeki işlemler üzerine dağılma özelliği vardır.
\[ A \times (B \cap C) = (A \times B) \cap (A \times C) \]
\[ A \times (B \cup C) = (A \times B) \cup (A \times C) \]
\[ A \times (B \; – \; C) = (A \times B) \; – \; (A \times C) \]
\( 4) \quad \) Kartezyen çarpımın elaman sayısı:
\[ s(A \times B ) = s(B \times A) = s(A) \cdot s(B) \]
\( 5) \quad \) Kartezyen çarpımda
\[ A \times A = A^2, \quad A \times A \times A = A^3 \] şeklinde gösterilir.
Soru 3
\[ A= \{ x \; | \; -3 < x < 5, \;\; x \in Z \} \] ve \[ B = \{ x \; : \; |x | ≤ 2, \;\; x \in Z \} \] ise \( s( A \times B) \) kaçtır
Not: B kümesinde kullanılan ” : ” işareti ile A Kümesinde kullanılan ” | ‘ işaret ‘öyle ki’ anlamına gelir. B kümesinde mutlak değer ile karışmaması için ‘” : ” tercih edildi.
\[
\text{A)} 22 \quad
\text{B) } 25 \quad
\text{C) } 28 \quad
\text{D) } 30 \quad
\text{E) } 35
\]
Çözüm:
\[-3 < x < 5 \quad \text{ve } \quad x\in Z \quad \text{olduğundan} \]
\[ A = \{ -2, -1, 0, 1 , 2, 3, 4 \} \quad \text{ve } \quad s(A) = 7 \;\; \text{olur} \]
\[ |x| ≤ 2 \Rightarrow -2 ≤ x ≤ 2 \quad \text{ve } x \in Z \;\; \text{olduğundan } \]
\[ B = \{-2, -1, 0, 1, 2 \} \quad \text{ve} \quad s(B)= 5 \;\; \text{olur} \]
o halde,
\[ s( A \times B )= s(A) \cdot s(B) = 7 \cdot 5 = 35 \]
\(\textbf{Cevab: E} \)
Soru 4
\[ s ( ( A \times B) \cap (A \times C) )= 6 \quad \text{ve } \quad s(B \cap C) = 2 )\] ise, \( s(A) \) kaçtır?
\[
\text{A)} 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 6
\]
Çözüm:
\[ s(A \times B ) \cap s(A \times C) = 6 \Rightarrow s(A \times (B \cap C) = 6 \]
\[ \Rightarrow s(A) \cdot s( B \cap C ) = 6 \]
\[\Rightarrow s(A) \cdot 2 = 6 \]
\[ \Rightarrow s(A)= 3 \]
\(\textbf{Cevab: C} \)
Kartezyen Çarpımın Grafiği:
Kartezyen çarpımın grafiğine geçmeden önce dik koordinat sistemi hakkında bilgi verelim. Başlangıç (sıfır) noktalarından birbirine dik olarak çizilen iki sayı ekseninin, bir düzlemde meydana getirdiği sisteme dik koordinat sistemi (kartezyen koordinat sistemi) denir.
\(\bullet \quad Ox \) yatay eksenine apsisler ekseni,
\( \bullet \quad Oy \) düşey eksenine ise ordinatlar ekseni adi verilir.
Düzlemdeki bir \( P \) noktası \( (a, b )\) sıralı ikilisi ile temsil ediliyorsa \( P(a,b) \) biçiminde gösterilir. \( (a, b )\) sıralı ikilisine \( P \) nin koordinatları, \(a \) sayısına \( P \) nin apsisi ve \( b\) sayısına \( P\) nin ordinatı denir.
\( Ox\) ekseni üzerinde apsisi a olan noktadan \( Ox\) eksenine, \( Oy\) ekseni üzerinde ordinatı \( b\) olan noktadan \( Oz\) eksenine çıkılan dikmelerin kesiştiği nokta \(P(a,b) \) dir.
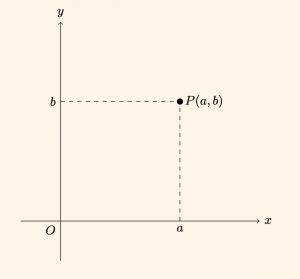
Bu sekilde, her \( (x,y) \; \in R \times R \) sıralı ikilisine düzlemde bir tek \(P \) noktası karşılık gelir. Böylece düzlemin noktaları \( R \times R\) kartezyen çarpımını meydana getirir.
Burada eksenlerin kesişim noktası. olan \( O\) başlangıç noktası (Orjin) \( (0, 0) \) sıralı ikilisine karşılık gelir.
Bu bilgilere göre \(A \times B \) nin grafiğini çizmek için \( A\) nın elemanları yatay eksen ( \(Ox \) ekseni) üzerinde alınır ve bu noktalardan yatay eksene, \( B\) nin elemanları düşey eksen (\( Oy\) ekseni) üzerinde alınır ve bu noktalardan düşey eksene dikmeler çıkılır. Bu dikmelerin düzlemdeki kesişim noktalarının kümesi \( A \times B \) nin grafiğini verir.
Örnek:
\( A= \{ 1,2,3 \} \) ve \( B = ( -1, 2 ] \) ise \( A \times B \) nin grafiğini çizelim.
Yatay eksende apsisi \( 1, 2\) ve \( 3\) olan noktalardan yatay eksene dikmeler çıkılır. Düşey eksende ordinatı \(-1 \) (hariç) ile \( 2\) (dahil) arasındaki reel sayılar olan noktalardan düşey eksene dikmeler çıkılır. Bu dikmelerin kesişim noktalarının kümesi \( A \times B \) nin grafiğini verir.
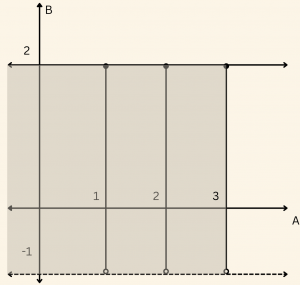
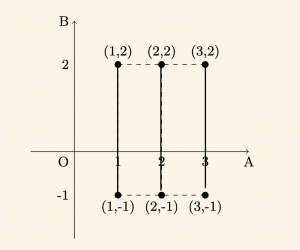
Şekildeki üç tane doğru parçası \( A \times B \) nin grafiğidir.
Örnek:
\( A= \{1,2,3\} \) ve \( B = [-1, 2] \) ise \(B \times A \) nın grafiğini çizelim.
Yatay eksende apsisi -1 (dahil) ile 2 (dahil) arasındaki reel sayılar olan noktalardan yatay eksene dikmeler çıkılır. Düşey eksende ordinatı 1 (hariç) ile 3 (dahil) arasındaki reel sayılar olan noktalardan düşey eksene dikmeler çıkılır. Bu dikmelerin kesişim noktalarının kümesi \( B \times A \) nın grafiğini verir.
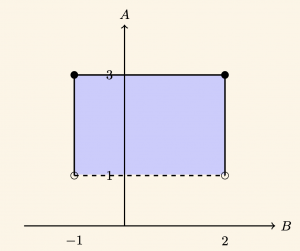
Şekildeki alan \( B \times A \) nın grafiğidir.
Örnek:
\( A = (1, 3] \) ise \( A \times A \) nın grafiğini çizelim.
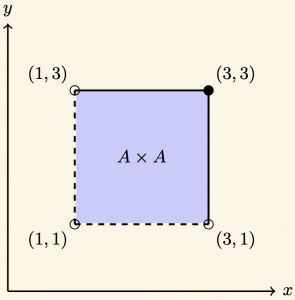
Örnek:
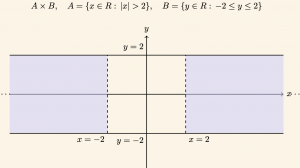
\( A= \{ x: |x| > 2, x \in R \}\) ve \( B = \{y | -2≤ y≤ 2, y \in R \) olduğuna göre \( A \times B \) nin grafiğini çizelim.
\[ |x| >2 \Rightarrow x > 2 \quad \text{vaya} \quad x < -2 \quad \text{olduğundan, } \]
\[ A = (-\infty, -2 ) \cup (2, \infty) \quad \text{ve } \quad B= [-2,2 ] \]
← Önceki Sayfa | Sonraki Sayfa →