Bağıntının Grafiği
Bir bağıntının elemanlarına, analitik düzlemde karşılık gelen noktaların kümesine bu bağıntının grafiği denir.
Bir bağıntının grafiğini çizmek için kartezyen çarpımının grafiğini çizerken izlenen yol takip edilir. Çünkü bağıntı, kartezyen çarpımın alt kümesidir.
Örnek:
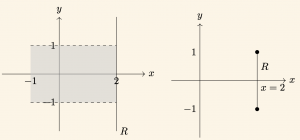
\[ R = \{(x,y) |\; x = 2 \quad \text{ve } \quad |y|= 1, \;\; (x,y ) \in R \times R \}\] bağıntısının grafiğini çizelim.
\[x= 2 \quad \text{ve } \quad |y| ≤ 1 \Rightarrow -1 \leq y \leq 1 \]
Örnek:
\(\mathbb{R} \times \mathbb{R} \) üzerinde tanımlı bir bağıntı olarak, Bağıntı \( R \;=\;\{(x,y)\in \mathbb{R} \times \mathbb{R} (\text{veya}\; \mathbb{R}^2) : |x| \le 2,\,-1 < y < 1\}\)
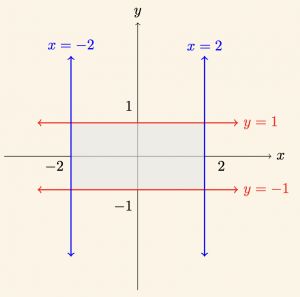
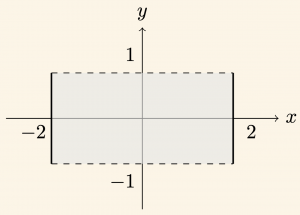
\[ x= 2 \quad \text{ve } |y| ≤1 \Rightarrow -1≤ y≤ 1 \] bağıntının, \( \mathbb{R}^2 \) üzerindeki grafiği ve kesişimler şekillerde gösterildiği gibidir. (Kesişimleri alttaki grafik)
Örnek:
\( \mathbb{R}^2 \) (Reel Sayılar ) Kümesinde tanımlı \( R \; = \{ (x, y) | \; y ≥ x \quad \text{ve } \; x > 1 \} \) bağıntısının grafiğini çizelim.
\[
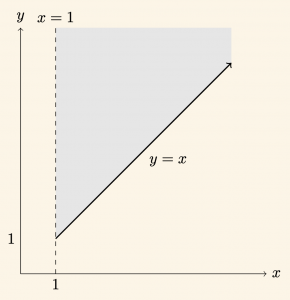
R \;=\;\bigl\{(x,y)\in \mathbb{R}^2 | x>1,\; y \ge x \bigr\}.
\]
Örnek:
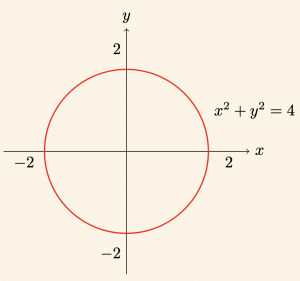
\( \mathbb{R}^2 \) (Reel Sayılar ) Kümesinde tanımlı \( R \; = \{ (x, y) | \; x^2+ y^2 = 4 \} \) bağıntısının grafiğini çizelim.
\(x^2+ y^2 = 4 \) eşitliğini sağlayan ikililerin kümesi merkezi orjinde, yarıçapı 2 birim olan bir çember belirtir.
Uyarı:
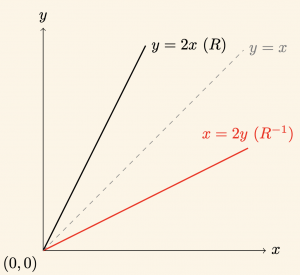
\(R \) bağıntısının grafiği ile bunun tersi olan \(R^{-1} \) bağıntısının grafiği \(y= x \) doğrusuna göre simetriktir.
Örnek:
\( \mathbb{R}^+ \cup \{0\} \) de tanımlı \( R = \{ (x,y) | y = 2x \) bağıntısı ile \( R^{-1} = \{ (x,y) | x = 2y \) ters bağıntısının grafiğini çizelim.
