Bağıntının Özellikleri

1. Yansıma Özelliği:

$R, \; A $ da tanımlı bir bağıntı olsun. $\forall \; x \in A $ için $ (x, x) \in R $ ise bağıntısının yansıma özelliği vardır veya $ R$ yansıyan bir bağıntıdır denir.

Not: $\forall$ işareti “her” anlamında kullanılan matematiksel bir semboldür.

Örnekler:

$\bullet \quad R_1 = \{ (a,a), (a, b), (b,b) \} $ bağıntısı $ c \in A $ için $ (c, c ) \notin R_1 $ olduğundan yansıyan degildir.

$\bullet \quad R_2 = \{ (a,a), (a, c), (b,b), (c,c) \} $ bağıntısı yansıyanıdır.

Uyarı:

$R \subset A \times A$ ve $R = \{(x,y)\mid x \in A \text{ ve } y \in A\}$ bağıntısının yansıyan olup olmadığını anlamak için, bağıntıda $y$ yerine $x$ yazılır. Elde edilen sonuç $A$ kümesinde daima doğru ise bu bağıntı yansıyandır.

Örnek:

$R \subset \mathbb{R}^{-} \times \mathbb{R}^{-}$ ve $R= \{(x,y)\mid |y| + x = 0\}$ bağıntısının yansıyan olup olmadığını inceleyelim.

Bağıntıda $y$ yerine $x$ yazılırsa, $|x| + x = 0$elde edilir ve $x \in \mathbb{R}^{-}$ için, $-x + x = 0$ daima doğru olduğundan bu bağıntı yansıyandır.

Örnek:

$R \subset \mathbb{R} \times \mathbb{R}$ ve $R = \{(x,y) \mid y < x\}$ bağıntısının yansıyan olup olmadığını inceleyelim.

Bağıntıda $y$yerine $x$ yazılırsa, $x < x$ elde edilir ve $\forall x \in \mathbb{R}$ için yanlış olduğundan bu bağıntı yansıyan değildir.

Yansıyan bağıntı sayısı:

$s(A) = n$ olmak üzere, $A$ kümesinde tanımlanabilecek yansıyan bağıntı sayısı,
\[\Large 2^{n^2 – n}\] dir.

Örnek:

$A = \{1, 2, 3, 4, 5\}$ kümesinde \[2^{5^2 – 5} = 2^{20}\] tane yansıyan bağıntı tanımlanabilir.

2. Simetri Özelliği:

$R$, $A$ da tanımlı bir bağıntı olsun.
\[\forall (x,y) \in R \text{ için } (y,x) \in R \text{ ise } R \text{ bağıntısının simetri özelliği vardır veya } R \text{ simetrik bir bağıntıdır denir.} \]

Uyarı:

$(a,b)$ ikilisinin $y = x$ doğrusuna göre simetriği $(b,a)$ ikilisidir.

Bir bağıntının simetrik olması için bu bağıntıya ait her ikilinin simetriği bağıntıda bulunmalıdır. Bağıntıda bir tek ikilinin bile simetriği bulunmuyorsa, bu bağıntı simetrik değildir.

Örnekler:

$A = \{1, 2, 3, 4\}$ kümesinde tanımlı,

$\bullet $ $R_{1} = \{(1,1), (1,2), (2,3), (3,2)\}$ bağıntısı, $(1,2) \in R_{1}$ için $(2,1) \notin R_{1}$ olduğundan simetrik değildir.

$\bullet $ $R_{2} = \{(1,2), (1,3), (3,3), (3,1), (2,1)\} $ bağıntısı simetriktir.

$\bullet $$ R_{3} = \{(1,1), (2,2), (3,3)\} $ bağıntısı simetriktir.

Uyarı:

$R$ bağıntısı simetrik ise $R= R^{-1}$’dir.

Örnek:

$ A = \{ 1, 2 \} $ kümesinde tanımlı
$ R= \{ (1,1), (1,2), (2,2), (2,1) \} $ bağıntısı için,
$ R^{-1} = \{ (1,1), (2,1), (2,2), (1,2) \} $ ve $ R= R^{-1} $’dir.

Uyarı:

$ R\subset A \times A $ ve $ R= \{ (x,y) \mid x \in A $ ve $ y \in A \} $ bağıntısının simetrik olup olmadığını anlamak için bağıntıda $ x $ ile $ y $ nin yerleri değiştirilir. Elde edilen bağıntı, verilen bağıntı ile aynı ise bu bağıntı simetriktir.

Örnek:

$ R\subset Z \times Z $ ve $ R= \{ (x,y) : 5 \mid (x-y) \} $ $(x – y, 5 \text{ ile tam bölünür})$ bağıntısının simetrik olup olmadığını inceleyelim.

$ k \in Z $ olmak üzere,
\[ 5 \mid (x-y) \Rightarrow \frac{x – y}{5} = k \Rightarrow x – y = 5k \]
Bağıntıda $ x $ ile $ y $ nin yerleri değiştirilirse, $ y – x = 5k $ elde edilir. Bu verilen bağıntı ile aynı olduğundan $ R$ bağıntısı simetriktir.

Örnek:

$ R \subset Z \times Z $ ve $ R= \{ (x,y) \mid y = |x| \} $ bağıntısının simetrik olup olmadığını inceleyelim.

Bağıntıda $ x $ ile $ y $ nin yerleri değiştirilirse, $ x = |y| $ elde edilir. Bu bağıntı, verilen bağıntı ile aynı olmadığından $ R $ bağıntısı simetrik değildir.

Simetrik Bağıntı Sayısı:

$ s(A) = n $ olmak üzere, $ A $ kümesinde tanımlanabilecek simetrik bağıntı sayısı,
\[ \large \frac{n^2 + n}{2} \]’dir.

3. Ters Simetri Özelliği:

$R $ A da tanımlı bir bağıntı olsun.

\[x \neq y \quad \text{iken} \quad \forall (x, y ) \in R \quad \text{için} \quad (y, x )\neq R \quad \text{ise } \]

$R $ bağıntısının ters simetri özelliği vardır veya $ R$ ters simetriktir denir.

Bir bağıntının ters simetrik olması için simetriği kendisi olan $ (x, x) $ şeklindeki ikililer hariç, hiç bir ikilinin simetriği bağıntıda bulunmamalıdır.

Örnekler:

$A = \{ 1, 2, 3, 4, 5 \}$ kümesinde tanımlı,

$\bullet \quad R_{1} = \{ (1, 1), (2, 2), (1, 2), (3, 2), (2, 1) \}$ bağıntısı $(1, 2) \in R_{1}$ için $(2, 1) \in R_{1}$ olduğundan ters simetrik değildir.

$\bullet \quad R_{2} = \{ (1, 1), (1, 3), (2, 3), (3, 3) \}$ bağıntısı ters simetriktir.

Uyarı:

Simetrik olmayan bir bağıntının ters simetrik olacağı veya ters simetrik olmayan bir bağıntının simetrik olacağı sonucu çıkarılmamalıdır.

Örnek:

$A = \{ a, b, c, d \}$ kümesinde tanımlanan,

$R= \{ (a, a), (b, c), (c, d), (c, b) \}$ bağıntısı $(c, d) \in R$ için $(d, c) \notin R$ olduğundan simetrik değildir. $(b, c) \in R$ için $(c, b) \in R$ olduğundan ters simetrik de değildir.

Örnek:

$A = \{ 1, 2, 3 \}$ kümesinde tanımlanan,

$R= \{ (1, 1), (2, 2), (3, 3) \}$ bağıntısı hem simetrik hem de ters simetrik bir bağıntıdır.

Uyarı:

$R\subset A \times A$ ve $R= \{ (x, y) \mid x \in A \text{ ve } y \in A \}$ bağıntısının ters simetrik olup olmadığını anlamak için bağıntıda $x$ ile $y$ nin yerleri değiştirilir. Elde edilen bağıntı $x \neq y$ iken, verilen bağıntıyla ortak çözülür. Çözüm kümesi boş küme ise bu bağıntı ters simetriktir.

Örnek:

$R\subset Z \times Z$ ve $R= \{ (x, y) \mid x^2 + 3y = 7 \}$ bağıntısının ters simetrik olup olmadığını inceleyelim.

Bağıntıda $x$ ile $y$ nin yerlerini değiştirelim.

\[y^2 + 3x = 7\quad\text{ve} \quad x^2 + 3y = 7\]
bağıntısı ile ortak çözülürse,

\[ y^2 + 3x = x^2 + 3y \quad \]
\[ \Rightarrow \quad y^2 – x^2 + 3x – 3y = 0 \]

\[\Rightarrow (y – x)(y + x) – 3(y – x) = 0 \]

\[ \Rightarrow (y – x)(y + x – 3) = 0 \]

\[ y \neq x \text{ için,} \Rightarrow y + x – 3 = 0 \quad \text{ve} \quad y = 3 – x \]
verilen bağıntıda yerine yazılırsa,
\[= x^2 + 3y = 7 \]

\[\Rightarrow x^2 + 3(3 – x) = 7 \]

\[ \Rightarrow x^2 – 3x + 9 = 7 \]

\[ \Rightarrow x^2 – 3x + 2 = 0 \]

\[ \Rightarrow(x – 1)(x – 2) = 0 \]

\[
x_1 = 1 \quad\text{veya}\quad x_2 = 2
\]
değerleri verilen bağıntıda yerine yazılırsa,
\[
y_1 = 2
\quad\text{veya}\quad
y_2 = 1
\]
O halde, $(1,2)$ ve $(2,1)$ ikilileri bağıntıya ait olduğundan bu bağıntı ters simetrik değildir.

4. Geçişme Özelliği:

$R$, $A$ da tanımlı bir bağıntı olsun.

$ \forall(x,y)\in R $ ve $ \forall(y,z) \in R \text{ için } $ $ (x,z) \in R $ ise $ R $ bağıntısının geçişme özelliği vardır veya $ R$ bağıntısı geçişkendir denir. $(x,y) \in R $ için bağıntıda $y$ ile başlayan ikili yoksa, $ (x,y)$ ikilisi geçişkenliği bozmaz.

Örnekler:

$A = \{ 1, 2, 3, 4 \} $ kümesinde tanımlı,

$ \bullet $ $R_1 = \{ (1,1), (1,2), (2,3), (1,3), (2,4) \} $ bağıntısı $ (1,2) \in R_1 $ ve $ (2,4) \in R_1 $ için $ (1,4) \notin R $ olduğundan geçişken değildir.

$ \bullet $ $R_2 = \{ (2,1), (1,2), (2,2), (2,3) \} $ bağıntısı $(1,2) \in R_2$ ve $(2,3)\in R_2$ için $(1,3) \notin R_2$ olduğundan geçişken değildir.

$ \bullet $ $R_3 = \{ (1,3), (2,4), (4,3), (1,2), (2,3) \} $ bağıntısı $ (1,2) \in R_3 $ ve $ (2,4) \in R_3 $ için $ (1,4) \notin R_3$ olduğundan geçişken değildir.

$ \bullet $ $R_4 = \{ (1,1), (1,3), (3,4), (1,4) \} $ bağıntısı geçişkendir.

$ \bullet $ $R_5 = \{(1,1), (2,3), (2,4)\} $ bağıntısı geçişkendir.

$ \bullet $ $R_6 = \{(3,4)\} $ bağıntısı geçişkendir.

Uyarı:

$ R \subset A \times A $ ve $ R = \{(x,y) \mid x \in A \text{ ve } y \in A\} $ bağıntısının geçişken olup olmadığını anlamak için bağıntıda $ x $ yerine $ y $, $ y $ yerine $ z $ yazılarak, elde edilen bağıntı verilen bağıntıyla ortak çözülür ve $ (x,z) \in R $ olduğu gösterilebilirse bu bağıntı geçişkendir.

Örnek:

$ R \subset \mathbb{Z} \times \mathbb{Z} $ ve $ R = \{(x,y) \mid x – y = k, \ k \in \mathbb{Z} \} $ bağıntısının geçişken olup olmadığını inceleyelim.

Bağıntıda $ x $ yerine $ y $, $ y $ yerine $ z $ yazalım.

\[
\begin{aligned}
& y – z = n \quad (n \in \mathbb{Z}) \\
+ \quad & x – y = k \\
\hline \\
& x – z = n + k
\end{aligned}
\]

ve $ (n + k) \in \mathbb{Z} $ olduğundan, $ (x,z) \in R $ dir.

O halde bu bağıntı geçişkendir.

Uyarı:

Kartezyen çarpımın grafiğinde $ y = x $ doğrusuna köşegen denir.

Grafiği verilen bir bağıntının;

$1.) $ Yansıyan olması için köşegen üzerindeki noktaların tamamı bağıntıya ait olmalıdır.
$2.) $ Simetrik olması için grafik köşegene göre simetrik olmalıdır.
$3.) $ Ters simetrik olması için köşegen üzerindeki noktalar hariç, köşegene göre simetrik hiç bir noktası olmamalıdır.

Örnek:

$ A = \{1, 2, 3\} $ olmak üzere,

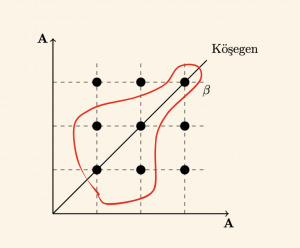
$ R $ bağıntısının yansıma ve simetri özelliği vardır.

Örnek:

$ A = \{1, 2, 3, 4 \} $ olmak üzere,

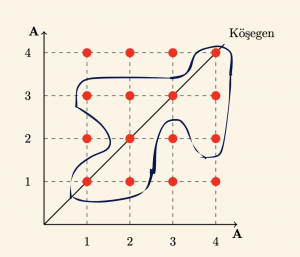
$ R $ bağıntısının yansıma ve ters simetri özelliği vardır.

Denklik Bağıntısı:

$ R$ A da tanımlı bir bağıntı olsun. Eger $ R$ nin yansıma, simetri ve geçişme özellikleri varsa; $R $ A da bir denklik bağıntısıdır denir. $ R$ denklik bağıntısında $ (x, y) \in R $ ise $x $ ve $ y$ elemanlarına $R $ bağıntısına göre birbirine denktir denir ve $ x \equiv y $ şeklinde gösterilir.

Örnek:

$ A = \{ x \mid -20 < x < 20, x \in \mathbb{Z} \} $ kümesinde tanımlı, $ R= \{ (x, y) \mid x – y = 2k, k \in \mathbb{Z} \} $ bağıntısının denklik bağıntısı olduğunu gösterelim.

$ 1) $ Bağıntıda $ y $ yerine $ x $ yazılırsa, $ x – x = 2k $ elde edilir ve $ k \in \mathbb{Z} $ olduğundan bağıntı yansıyandır.

$ 2) $ Bağıntıda $ x$ ile $y $ nin yerleri değiştirilirse, $y-x= 2k $ elde edilir. Bu bağıntı verilen bağıntı ile aynı olduğundan bağıntı simetriktir.

$ 3) $ Bağıntıda $ x$ yerine $ y $, $ y $ yerine $z $ yazalım

\[\begin{aligned} &y-z= 2n \quad (n \in Z ) \\+ \quad & x-y = 2k \\ \hline \\ &x-z= 2(n+k) \end{aligned}\]

ve $ n+k \in Z $ olduğundan, $ (x, z) \in R $ dir. O halde bağıntı geçişkendir. Buna göre, $ R$ bağıntısı denklik bağıntısıdır.

Örnek:

Bir düzlemdeki doğruların kümesi A olsun. A kümesinde tanımlanan $R $ “doğruların paralelliği” bağıntısının denklik bağıntısı olduğunu gösterelim.

Bu bağıntı birbirine paralel veya çakışık doğru ikililerinden meydana gelmektedir. Buna göre,

$d_1 \in A, \quad d_2 \in A \quad \text{ve} \quad d_3 \in A$ ise,

$ 1) $ $ d_1 \parallel d_1 , \quad d_2 \parallel d_2 \dots \Rightarrow (d_1, d_1) \in R, $ ve $ (d_2, d_2) \in R $ olduğundan $ R $ yansıyandır.

$ 2) $ $d_1 \parallel d_2 $ ise $ d_2 \parallel d_1 \dots \Rightarrow (d_1, d_2) \in R$ için, $(d_2, d_1) \in R$ olduğundan $ R $ simetriktir.

$ 3) $ $ d_1 \parallel d_2 $ ve $ d_2 \parallel d_3 $ ise $ d_1 \parallel d_3 \dots \Rightarrow $ $(d_1, d_2) \in R$, $(d_2, d_3) \in R $ için $ (d_1, d_3) \in R$ … olduğundan $ R $ geçişkendir. O halde $ R $ bağıntısı denklik bağıntısıdır.

Denklik Sınıfı:

$ R $ , A’da tanımlı bir denklik bağıntısı olsun. A’nın herhangi bir $ x$ elemanına $ R$ ile bağlı olan A’nın tüm elemanlarının kümesine $ x$ ‘in denklik sınıfı denir ve $ \bar{x} $ ile gösterilir. Buna göre,

\[
\bar{x} = \{ y \mid (x, y) \in R, \;R \text{ denklik bağıntısı} \}
\]

Örnek:

\[
A = \{ 0, 1, 2, 3, 4 \} \text{ kümesinde tanımlı,}
\]

\[
R= \{ (x, y) : 3 \mid (x – y) \} \quad \text{(3, $x – y$’yi böler)}
\]

Bağıntısının denklik bağıntısı olduğunu göstererek 1 ve 2 sayılarının denklik sınıflarını bulalım.

\[
3 \mid (x – y) \Rightarrow \frac{x – y}{3} = k \quad (k \in \mathbb{Z})
\]

O halde,

\[ R= \{ (0,0), (0,3), (1,1), (1,4), (2,2), (3,0), (3,3), (4,1), (4,4) \} \]

olduğundan $ R $ ‘nın yansıma, simetri ve geçişme özelliği vardır. O halde $R $ denklik bağıntısıdır.

\[ \bar{1} = \{1,4\}, \quad \bar{2} = \{2\} \text{ dir.} \]

Uyarı:

$ R $, $ A $ kümesinde tanımlı bir denklik bağıntısı olsun. $ R $, $ A $ kümesini denklik sınıflarına ayırır. Yani denklik sınıflarının birleşimi A kümesine eşittir. Yukarıdaki örnekte,

\[ \bar{0} = \{0,3\} \]
\[\bar{1} = \{1,4\}\]
\[\bar{2} = \{2\}\]
\[A = \bar{0} \cup \bar{1} \cup \bar{2} = \{0,1,2,3,4\}\]

SORU 8

\[
R = \{ (x,y) \mid x^2 + x = y^2 + y, \quad (x,y) \in \mathbb{Z} \times \mathbb{Z} \}
\] denklik bağıntısıdır.

Buna göre, 1’in denklik sınıfı nedir?

\[
\text{A)} \{ 1,2 \} \quad
\text{B) } \{ -1, 1 \} \quad
\text{C) } \{ 1 \} \quad
\text{D) } \{ -3,1 \} \quad
\text{E) } \{ -2, 1 \}
\]

Çözüm:

1’in denklik sınıfı bulunurken, bağıntıda $ x = 1 $ için $y $’nin alabileceği değerlerin kümesi bulunur.

\[ x^2 + x = y^2 + y \Rightarrow 1^2 + 1 = y^2 + y \]

\[ \Rightarrow y^2 + y – 2 = 0 \]

\[ \Rightarrow (y – 1)(y + 2) = 0 \]

\[ \Rightarrow y_1 = 1 \quad \text{veya} \quad y_2 = -2 \]

O halde,

\[ \bar{1} = \{-2,1\} \]

$\textbf{Cevab: E} $

Sıralama Bağıntısı:

$R $ , $ A$ ‘da tanımlı bir bağıntı olsun. Eğer $R $ ‘nın yansıma, ters simetri ve geçişme özellikleri varsa; $R $ , $A $ ‘da bir sıralama bağıntısıdır.

Örnek:

\[
R = \{ (x, y) \mid x \geq y, (x, y) \in \mathbb{R} \times \mathbb{R} \}
\]

bağıntısının sıralama bağıntısı olduğunu gösterelim.

$ 1) $ $x \geq y $ verildiğine göre $x \geq x $ olduğundan $ \forall x \in \mathbb{R} \text{ için } (x, x) \in R \text{ dir}
$. O halde $ R $ yansıyandır.

$ 2) $ $ x \neq y $ olmak üzere $x \geq y$ için $y \geq x $ olamaz. Buna göre bileşenleri birbirinin aynısı olan ikililer dışında hiçbir ikilinin simetriği yoktur. O halde $ R $ ters simetriktir.

$ 3) $ $x \geq y $ ve $ y \geq z $ için $ x \geq z $ olacağından $ R $ geçişkendir. Buna göre, $ R $ sıralama bağıntısıdır.

Örnek:

Kan grupları kümesi üzerinde birinin diğerine kan verebilmesi bağıntısı tanımlanıyor. Bu bağıntı $ R$ ile gösterilsin. $ R$ ‘nın sıralama bağıntısı olduğunu gösterelim.

\[R= \{ (A,A), (O,O), (B,B), (AB,AB), (A,AB), (O,B), (B,AB), (O,AB), (O,A) \} \]

$ R$ bağıntısı yansıma, ters simetri ve geçişme özelliklerine sahip olduğundan sıralama bağıntısıdır.