İkinci Dereceden Fonksiyonların Grafikleri
\( a, b, c, x \in \mathbb{R} \) ve \( a \neq 0 \) olmak üzere,
\[
f : \mathbb{R} \to \mathbb{R}, \quad f(x) = ax^2 + bx + c
\]
şeklinde tanımlanan fonksiyonlara ikinci dereceden bir değişkenli fonksiyonlar denir. Bu tür fonksiyonların grafikleri parabol adı verilen eğrilerdir.
\( f(x) = ax^2 + bx + c \) fonksiyonunda \( b = 0 \) ve \( c = 0 \) alınırsa \( f(x) = ax^2 \) fonksiyonu elde edilir. Şimdi de bu fonksiyonun grafiğini çizelim.
\( y = f(x) = ax^2 \) fonksiyonunda \( x \) in her değeri için \( y \) nin aldığı değerler hesaplanabilir. Ancak, kabaca çizim yapabilmek için \( x \) in aldığı değişik değerlere karşılık \( y \) nin alacağı değerleri gösteren tablo yapılarak grafik çizilir.
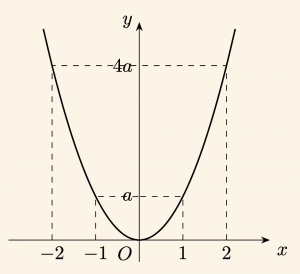
1) \( y = f(x) = ax^2 \) ve \( a > 0 \) ise,
\[
\begin{array}{c|ccccccc}
x & -\infty & -2 & -1 & 0 & 1 & 2 & +\infty \\ \hline
y =f(x)= ax^2 & +\infty \; \searrow & 4a\searrow & a \searrow& 0 \nearrow& a \nearrow& 4a \nearrow& +\infty
\end{array}
\]
\[
\text{Parabol } y = ax^2 \text{ (}a>0\text{) grafiği, kolları yukarı doğru olan bir eğridir.}
\]
\( a> 0\) ve \( \forall x \in \mathbb{R} \) için \( y = f(x) = ax^2 ≥ 0 \) olduğundan parabolün kolları Oy ekseninin pozitif yönündedir. Bu durumda parabolün en alt noktası olan \(0(0, 0) \) noktasına parabolün tepe noktası denir.
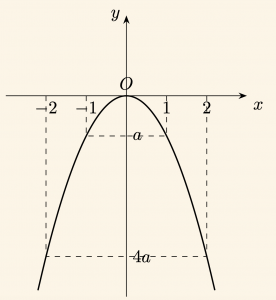
2) \( y = f(x) = ax^2 \) ve \( a < 0 \) ise,
\[
\begin{array}{c|ccccccc}
x & -\infty & -2 & -1 & 0 & 1 & 2 & +\infty \\ \hline
y =f(x)= ax^2 & +\; \nearrow & 4a\nearrow & a \nearrow& 0 \searrow& a \searrow& 4a \searrow& +\infty
\end{array}
\]
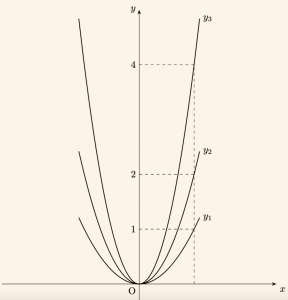
Örnek:
\( y_1= x^2, \;\; y_2= 2x^2 \) ve \( y_3= 4x^2\) parabollerini ayni analitik düzlemde çizelim.
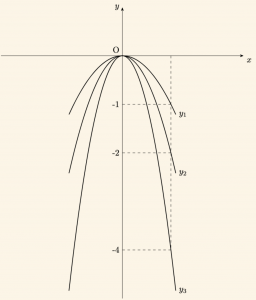
Örnek:
\( y_1= -x^2, \;\; y_2= -2x^2 \) ve \( y_3= -4x^2\) parabollerini ayni analitik düzlemde çizelim.
Sonuç:
\( f(x) = ax^2 + bx + c \) de,
\(\bullet \quad |a| \) büyüdükçe parabolün kolları Oy eksenine yaklaşır (kollar daralır).
\(\bullet \quad |a| \) küçüldükçe parabolün kolları Oy ekseninden uzaklaşır (kollar açılır).
SORU 1
Yandaki şekilde \( y = 2mx^2 \) parabolü verilmiştir.
– \( [OA] \perp [AB] \),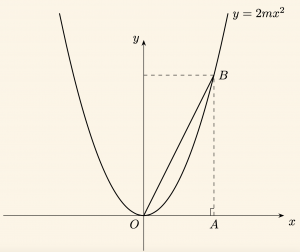
– \( |AB| = 2|OA| \) ve
– \( |OB| = \sqrt{10} \) birim olduğuna göre, m kaçtır?
\[
\text{A) } \sqrt{ 2} \quad
\text{B) }\frac{\sqrt{ 2}}{2} \quad
\text{C) } 2 \quad
\text{D) } 4 \quad
\text{E) } 8
\]
Çözüm:
\( |OA| = a \) olsun.
\( |AB| = 2a \) olur.
\( OAB \) dik üçgeninde Pisagor bağıntısı uygulanırsa,
\[
a^2 + (2a)^2 = (\sqrt{10})^2
\]
\[
a^2 + 4a^2 = 10
\]
\[
\Rightarrow 5a^2 = 10
\]
\[
\Rightarrow a = \sqrt{2}
\]
bulunur.
O halde \( B(a, 2a) \) olduğundan \( B(\sqrt{2}, 2\sqrt{2}) \) olur. Bu nokta parabolün denklemini sağlayacağından,
\[
y = 2mx^2 \Rightarrow 2\sqrt{2} = 2m (\sqrt{2})^2
\]
\[
\Rightarrow m = \frac{\sqrt{2}}{2}
\]
dir.
\(\textbf{Cevab: B} \)
SORU 2
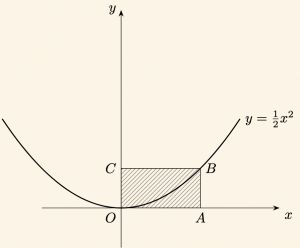Yandaki şekilde
\[
y = \frac{1}{2} x^2
\]
parabolü verilmiştir.
OABC karesinin alanı kaç birim karedir?
\[
\text{A) } \frac{1}{4} \quad
\text{B) }\frac{1}{2} \quad
\text{C) } 1 \quad
\text{D) } 2 \quad
\text{E) } 4
\]
Çözüm:
OABC karesinin bir kenarının uzunluğu \( k \) birim olsun. Bu durumda B noktasının apsisi ve ordinatı \( k \) olur.
\( B(k,k) \) noktası parabol üzerinde olduğundan, parabolün denklemini sağlar.
O halde,
\[
y = \frac{1}{2} x^2 \quad \text{ de } \quad x = k \quad \text{ için } \quad y = k = \frac{1}{2} k^2
\]
\[
\Rightarrow k = 2
\]
\[
\Rightarrow A(OABC) = k^2 = 4 \quad \text{ birim karedir.}
\]
\(\textbf{Cevab: E} \)
\( y = f(x) = ax^2 + bx+c \) Fonksiyounun Grafiği
\( f : \mathbb{R} \to \mathbb{R} \), \( y = f(x) = ax^2 + bx + c \) fonksiyonunun grafiğini (parabol) çizebilmek için yapılması gereken işlemleri sıralayalım.
1) Parabolün kollarının yönü tespit edilir
\( \bullet \quad a > 0 \) ise parabolün kolları Oy ekseninin pozitif yönünde,
\( \bullet \quad a < 0 \) ise parabolün kolları Oy ekseninin negatif yönündedir.
Örnek:
\[
y = f(x) = x^2 – 4x + 3
\]
parabolünün kolları \( a = 1 > 0 \) olduğundan Oy ekseninin pozitif yönündedir.
2) Parabolün tepe noktasının koordinatları bulunur:
\( ax^2 + bx + c \) üç terimlisi tam kare yapılırsa.
\[
f(x) = ax^2 + bx + c
\]
\[
= a(x + \frac{b}{2a})^2 + \frac{4ac – b^2}{4a}
\]
olur.
Burada,
\[
-\frac{b}{2a} = r \quad \text{ve} \quad \frac{4ac – b^2}{4a} = k
\]
denilirse,
\[
f(x) = ax^2 + bx + c = a(x – r)^2 + k
\]
parabolünün \( T(r, k) \) tepe noktasının koordinatları,
\[
r = -\frac{b}{2a} \quad \text{ve} \quad k = \frac{4ac – b^2}{4a}
\]
dir.
Örnek:
\[
y = x^2 – 4x + 3
\]
parabolünün tepe noktasının koordinatlarını bulalım.
\[
r = -\frac{b}{2a} =-\frac{-4}{2 \cdot 1} = \frac{4}{2} = 2
\]
\[
k =\frac{4ac – b^2 }{4a} = \frac{4(1)(3) – (-4)^2}{4(1)}
\]
\[
= \frac{12 – 16}{4} = \frac{-4}{4} = -1
\]
Buradan, \( T(2, -1) \) bulunur.
Uyarı:
\( f(x) = ax^2 + bx + c \) parabolünün tepe noktası \( T(r, k) \) olmak üzere, bu nokta parabolün denklemini sağlayacağından,
\[
k = f(r)
\]
olarak da bulunabilir.
3) Parabolün Ox eksenini kestiği noktaların (varsa) koordinatları bulunur:
Parabolün Ox eksenini kestiği noktalar ordinatı \( y = 0 \) olan noktalardır.
\[
y = ax^2 + bx + c = 0
\]
Bu denklemin reel kökleri (varsa) \( x_1, x_2 \) olsun.
a) \( \Delta > 0 \) ise parabol, Ox eksenini \( (x_1, 0) \) ve \( (x_2, 0) \) gibi farklı iki noktada keser.
b) \( \Delta = 0 \) ise parabol, Ox eksenine teğettir.
c) \( \Delta < 0 \) ise parabol, Ox eksenini kesmez.
Örnek:
\[
y = x^2 – 4x + 3
\]
parabolü için,
\[
\Delta = b^2 – 4ac = (-4)^2 – 4(1)(3) = 16 – 12 = 4 > 0
\]
olduğundan, parabol Ox eksenini iki farklı noktada keser. Bu noktalar,
\[
y = x^2 – 4x + 3 = 0 \Rightarrow x = 1 \quad \text{veya} \quad x = 3
\]
olduğundan,
\[
(1,0) \quad \text{ve} \quad (3,0)
\]
noktalarıdır.
4) Parabolün Oy eksenini kestiği noktanın koordinatı bulunur:
Parabolün Oy eksenini kestiği noktanın apsisi \( x = 0 \) olduğundan ordinatı \( y = c \) olur.
Buna göre, Parabol, Oy eksenini \( (0,c) \) noktasında keser.
Örnek:
\[
y = x^2 – 4x + 3
\]
parabolünün Oy eksenini kestiği nokta,
\[
x = 0 \text{ için } y = 3
\]
olduğundan,
\[
(0,3)
\]
noktasıdır.
Yukarıdaki işlemlerin sonucunda
\[ y = x^2 – 4x + 3\]
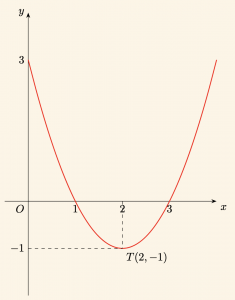
parabolü çizilmiştir.
Örnek:
\[
f(x) = -x^2 + 2x + 3
\]
parabolünü çizelim.
\( a = -1 < 0 \) olduğundan parabolün kolları Oy ekseninin negatif yönündedir. Parabolün Tepe Noktasının Koordinatları:
\[
r = -\frac{b}{2a} = \frac{-2}{2(-1)} = 1
\]
\[
k = f(1) = – (1)^2 + 2(1) + 3 = 4
\]
\[
\Rightarrow T(1, 4)
\]
Parabolün Ekseni Kestiği Noktalar:
Parabolün Ox eksenini kestiği noktalar için \( y = 0 \) alınır.
\[
– x^2 + 2x + 3 = 0
\]
\[
\Rightarrow x_1 = -1 \quad \text{veya} \quad x_2 = 3
\]
olduğundan, kesim noktaları:
\[
(-1, 0) \quad \text{ve} \quad (3, 0)
\]
Parabolün Oy eksenini kestiği nokta:
\[
x = 0 \text{ için } y = 3
\]
\[
\Rightarrow (0, 3)
\]
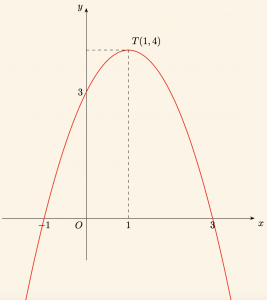
Örnek:
\[
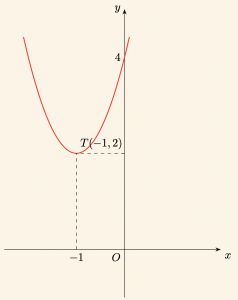
f(x) = 2(x + 1)^2 + 2
\]
parabolünü çizelim.
Parabolün Kollarının Yönü:
\[
y = a(x – r)^2 + k
\]
ifadesinden,
\[
a = 2 > 0
\]
olduğundan parabolün kolları Oy ekseninin pozitif yönündedir.
Parabolün Tepe Noktasının Koordinatları:
\[
r = -1 \quad \text{ve} \quad k = 2
\]
\[
\Rightarrow T(-1,2)
\]
Parabolün Ekseni Kestiği Noktalar:
Parabolün Ox eksenini kestiği noktalar için \( y = 0 \) alınır.
\[
2(x + 1)^2 + 2 = 0
\]
Buradan \( \Delta < 0 \) olduğundan parabol Ox eksenini kesmez.
Parabolün Oy eksenini kestiği nokta:
\[
x = 0 \text{ için } y = 4
\]
\[
\Rightarrow (0, 4)
\]
Örnek:
\[
f(x) = -x^2 – 2x – 1
\]
parabolünü çizelim.
Fonksiyon,
\[
y = -x^2 – 2x – 1
\]
şeklinde düzenlenirse,
\[
y = – (x + 1)^2
\]
formunda yazılabilir. Buradan,
\[
y = a(x – r)^2 + k
\]
şeklindeki ifadeyle karşılaştırıldığında,
\[
a = -1 < 0
\]
olduğundan parabolün kolları Oy ekseninin negatif yönündedir.
Parabolün Tepe Noktasının Koordinatları:
\[
r = -1 \quad \text{ve} \quad k = 0
\]
\[
\Rightarrow T(-1,0)
\]
Parabolün Ekseni Kestiği Noktalar:
Parabolün Ox eksenini kestiği noktalar için \( y = 0 \) alınır.
\[
– x^2 – 2x – 1 = 0
\]
\[
\Rightarrow x_1 = x_2 = -1
\]
olduğundan, parabol Ox eksenine teğettir ve kesim noktası:
\[
(-1, 0)
\]
Parabolün Oy eksenini kestiği nokta:
\[
x = 0 \text{ için } y = -1
\]
\[
\Rightarrow (0, -1) \quad \text{bulunur. }
\]
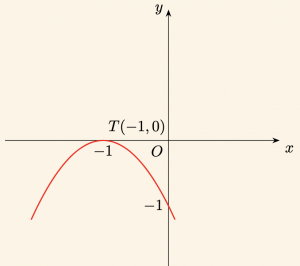
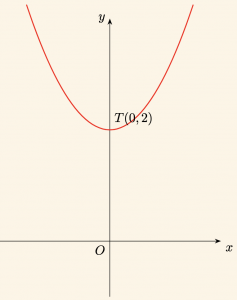
Örnek:
\[
y = x^2 + 2
\]
parabolünü çizelim.
Parabolün Kollarının Yönü:
\[
y = a(x – r)^2 + k
\]
ifadesinden,
\[
a = 1 > 0
\]
olduğundan parabolün kolları Oy ekseninin pozitif yönündedir.
Parabolün Tepe Noktasının Koordinatları:
\[
r = 0 \quad \text{ve} \quad k = 2
\]
\[
\Rightarrow T(0,2)
\]
Parabolün Ekseni Kestiği Noktalar:
Parabolün **Ox eksenini** kestiği noktalar için **\( y = 0 \)** alınır.
\[
x^2 + 2 = 0
\]
Buradan **\( \Delta < 0 \)** olduğundan **parabol Ox eksenini kesmez**.
Parabolün Oy eksenini kestiği nokta:
\[
x = 0 \text{ için } y = 2
\]
\[
\Rightarrow (0, 2)
\]
Sonuçlar:
1) \( y = ax^2 + bx + c \) parabolünün simetri ekseni:
\[
x = -\frac{b}{2a}
\]
doğrusudur.
\[
|AR| = |RB|, \quad |CQ| = |QD|, \quad |EP| = |PF|, \dots
\]
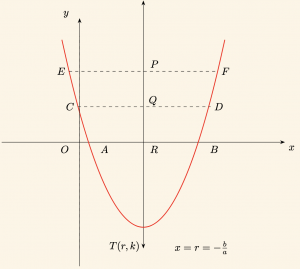
2) \( y = ax^2 + bx + c \) parabolünün Ox eksenini kestiği noktaların apsisleri \( x_1 \) ve \( x_2 \) olsun.
\[
r = -\frac{b}{2a}
\]
\[
x_1 + x_2 = -\frac{b}{a}
\]
\[
\Rightarrow r = \frac{x_1 + x_2}{2} \quad \text{dir. }
\]
3) \( a > 0 \) ise \( f(x) = ax^2 + bx + c \) parabolünün tepe noktası en alt noktasıdır, bu yüzden \( f(x) \)’in alabileceği en küçük değer:
\[
k = \frac{4ac – b^2}{4a}
\]
dır.
\( a < 0 \) ise \( f(x) = ax^2 + bx + c \) parabolünün tepe noktası en üst noktasıdır, bu yüzden \( f(x) \)’in alabileceği en büyük değer:
\[
k = \frac{4ac – b^2}{4a}
\]
dır.
4)
\[
y = ax^2 + bx + c = a(x – r)^2 + k
\]
fonksiyonunda,
a) \( r \neq 0 \) ve \( k = 0 \) ise tepe noktası \( T(r,0) \), Ox ekseni üzerindedir. (Parabol Ox eksenine teğettir.)
b) \( r = 0 \) ve \( k \neq 0 \) ise tepe noktası \( T(0,k) \), Oy ekseni üzerindedir. Oy ekseni, parabolün simetri eksenidir.
Burada:
\[
r = -\frac{b}{2a} = 0 \Rightarrow b = 0 \quad \text{olur. }
\]
c) \( r = 0 \) ve \( k = 0 \) ise tepe noktası \( T(0,0) \), orijindedir.
SORU 3
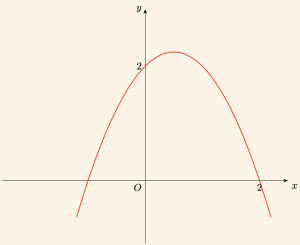Şekildeki parabolün denklemi
\[
f(x) = -x^2 + bx + c
\]
olduğuna göre, \( f(x) \)’in alabileceği en büyük değer nedir?
\[
\text{A) } 3 \quad
\text{B) } \frac{9}{4} \quad
\text{C) } \frac{9}{5} \quad
\text{D) } \frac{3}{2} \quad
\text{E) } \frac{9}{7}
\]
Çözüm:
\( y = -x^2 + bx + c \) parabolü ekseni \( (0,2) \) ve \( (2,0) \) noktalarında kestiğinden,
\( x = 0 \) için:
\[
y = c = 2
\]
\( x = 2 \) için:
\[
y = -4 + 2b + 2 = 0
\]
\[
\Rightarrow 2b – 2 = 0
\]
\[
\Rightarrow b = 1
\]
Parabolün denklemi:
\[
y = -x^2 + x + 2
\]
olarak bulunur. Buradan da parabolün alabileceği en büyük değer:
\[
k = \frac{4ac – b^2}{4a}
\]
\[
= \frac{4(1)(2) – (1)^2}{4(-1)}
\]
\[
= \frac{8 – 1}{-4} = \frac{9}{4} \quad \text{olarak bulunur. }
\]
\(\textbf{Cevab: B } \)
SORU 4
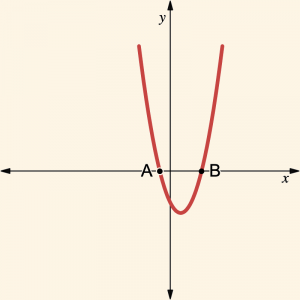
Şekildeki parabolün denklemi: \( y = x^2 – 2x + c\) ve \( |OB| = 3|OA| \) olduğuna göre, c kaçtır?
\[
\text{A) } -5 \quad
\text{B) } -4 \quad
\text{C) } -3\quad
\text{D) } -2 \quad
\text{E) } -1
\]
Çözüm:
Parabolün Ox eksenini kestiği noktalar A ve B’nin apsisleri sırasıyla \( x_1 \) ve \( x_2 \) olsun.
Eğer \( |OA| = m \) denirse, \( |OB| = 3m \) olur. Buradan:
\[
x_1 = -m, \quad x_2 = 3m
\]
Parabolün tepe noktası:
\[
r = \frac{x_1 + x_2}{2} = \frac{-m + 3m}{2} = m
\]
\[
r = \frac{-(-2)}{2(1)} = \frac{2}{2} = 1 \Rightarrow m = 1
\]
Buradan:
\[x_1 = -1, \quad \text{ve } \quad x_2 = 3\]
Çarpımları:
\[
x_1 \cdot x_2 = \frac{c}{1} \Rightarrow x_1 \cdot x_2= c = -3
\]
\(\textbf{Cevab: C} \)
SORU 5
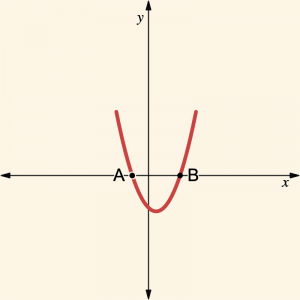
Şekildeki parabolün denklemi: \( y = mx^2 + (m – 2)x – 2 \) ve \( |AB| = 3 \) birim olduğuna göre, m kaçtır?
\[
\text{A) } \frac{1}{3} \quad
\text{B) } \frac{1}{2} \quad
\text{C) } 1\quad
\text{D) } 2 \quad
\text{E) } -3
\]
Çözüm 1:
\[
y = mx^2 + (m – 2)x – 2 = 0
\]
\[
\Rightarrow (x + 1)(mx – 2) = 0
\]
\[\Rightarrow x = -1 \quad \text{veya} \quad x = \frac{2}{m} \]
olduğundan \[ A(-1, 0 ) \quad \text{ve } \quad B(\frac{2}{m}, 0 ) \quad \text{olur.} \] O halde \[|AB| = |AO|+ |OB|= 3 \Rightarrow 1 + \frac{2}{m } = 3 \]
\[ \Rightarrow m= 1 \quad \text{bulunur. } \]
\(\textbf{Cevab: C} \)
Çözüm 2:
Parabolün Ox eksenini kestiği noktalar A ve B, sırasıyla \( x_1 \) ve \( x_2 \) olsun.
\[
|AB| = |x_2 – x_1| \Rightarrow 3 = \frac{\sqrt{\Delta}}{|a|}
\]
\[
\Rightarrow 3 = \frac{\sqrt{(m-2)^2 – 4m(-2)}}{|m|}
\]
\[
\Rightarrow 3 = \frac{|m + 2|}{|m|}
\]
\( a = m > 0 \) olduğundan,
\[
m + 2 = 3m
\]
\[
\Rightarrow m = 1
\]
\(\textbf{Cevab: C} \)
SORU 6
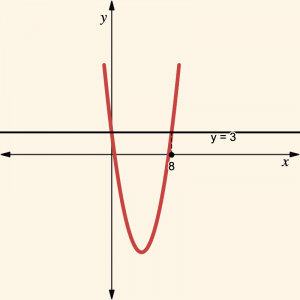
Yukarıdaki parabolün denklemi
\[
y = f(x) = x^2 + bx + c
\]
ise \( f(1) \) değeri kaçtır?
\[
\text{A) } 1 \quad
\text{B) } 0 \quad
\text{C) } -2\quad
\text{D) } -4 \quad
\text{E) } -5
\]
Çözüm:
Parabolün tepe noktası:
\[
r = -\frac{b}{2a}
\]
Tepe noktası \( r = 4 \) verildiğinden:
\[
4 = -\frac{b}{2 \cdot 1}
\]
\[
\Rightarrow b = -8
\]
Ayrıca, parabolün Oy eksenini kestiği noktanın ordinatı 3 olduğundan:
\[
c = 3
\]
olur. O halde, parabol denklemi:
\[
f(x) = x^2 + bx + c
\]
\[
\Rightarrow f(x) = x^2 – 8x + 3
\]
Bu durumda:
\[
f(1) = (1)^2 – 8(1) + 3
\]
\[
= 1 – 8 + 3 = -4
\]
\(\textbf{Cevab: D} \)
SORU 7
\[ y= \frac{m}{2}x^2+(m+2)x+2m-1 \]
\[ y= -x^2+2x+m+1 \]
olmak üzere. Yukarıdaki şekle göre AB uzunluğu kaç birimdir?
\[
\text{A) } 2 \quad
\text{B) } 3 \quad
\text{C) } 4\quad
\text{D) } 5 \quad
\text{E) } 6
\]
Çözüm:
Verilen parabol denklemleri:
\[
y = \frac{m}{2} x^2 + (m+2)x + 2m – 1
\]
ve
\[
y = -x^2 + 2x + m + 1
\]
Bu iki parabol Oy eksenini aynı noktada kestikleri için:
\[
2m – 1 = m + 1
\]
\[
\Rightarrow m = 2
\]
Bu değeri parabol denklemlerinde yerine yazarak Ox ekseni kesim noktalarını bulalım.
Parabol denklemi:
\[
y = \frac{m}{2} x^2 + (m+2)x + 2m – 1
\]
\[
\Rightarrow y = x^2 + 4x + 3 = 0
\]
Denklemin kökleri:
\[x = -3 \quad \text{veya} \quad x = -1
\]
Bu durumda:
\[
A(-3, 0)
\]
olur.
\[
y = -x^2 + 2x + m + 1 \Rightarrow y = -x^2 + 2x + 3 = 0
\]
\[
\Rightarrow x = -1 \quad \text{veya} \quad x = 3
\]
\[
\Rightarrow B(3,0) \quad \text{bulunur.}
\]
\[
|AB| = 3 – (-3) = 6 \quad \text{birimdir.}
\]
\(\textbf{Cevab: E} \)
SORU 8
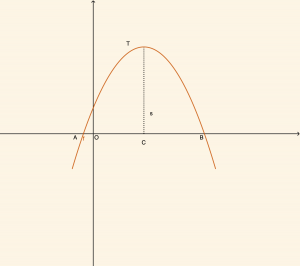
Yandaki şekilde tepe noktası \( T \) olan
\[
y = -x^2 + 2mx + 5m + 2
\]
parabolü verilmiştir.
\(|OC| = 3|OB|\) olup A, B ve C noktalarının apsisleri çarpımı \(-24 \) tür. Bu parabolün Oy eksenini kestiği noktanın ordinatı nedir?
\[
\text{A) } 8 \quad
\text{B) } 9 \quad
\text{C) } 10\quad
\text{D) } 11 \quad
\text{E) } 12
\]
Çözüm:
\[
|OB| = r \quad \text{denilirse} \quad |OC| = 3r \quad \text{olur.}
\]
A noktasının apsisi a olsun. Buradan noktalar:
\[
A(a,0), \quad B(r,0), \quad C(3r,0)
\]
elde edilir.
Parabolün simetri ekseni \( x = r \) olduğuna göre:
\[
r = \frac{a + 3r}{2} \Rightarrow a = -r
\]
Apsislerin çarpımı:
\[a \cdot r \cdot 3r = -24 \]
\[\Rightarrow r= 2 \quad \text{ve } \quad r = -\frac{2m}{2 \cdot (-1) } = 2 \] olduğundan \( m =2\) bulunur. Parabolün Oy eksenini kestiği noktanın ordinatı,
\[ 5m +2 = \Rightarrow 5 \cdot 2 + 2 = 12 \;\; \text{dir. } \]
SORU 9
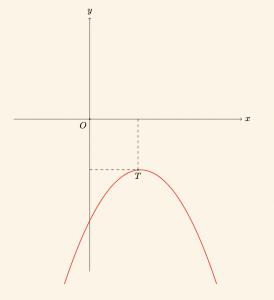
Yandaki şekilde tepe noktası T olan \[ y = ax^2 + bx + c \] parabolü verilmiştir.
Aşağıdakilerden hangisi yanlıştır.
\[
\text{A) } b^2 < 4ac \quad
\text{B) } a< 0 \quad
\text{C) } b > 0\quad
\text{D) } c< 0 \quad
\text{E) } ab + c >0
\]
Çözüm:
A) Parabol Ox eksenini kesmediğinden
\[
\Delta = b^2 – 4ac < 0 \Rightarrow b^2 < 4ac
\]
B) Parabolün kolları Oy ekseninin negatif yönünde olduğundan
\[
a < 0
\]
C) Parabolün tepe noktasının apsisi
\[
-\frac{b}{2a} > 0 \quad \text{ve } a < 0 \quad \text{olduğundan}
\]
\[
b > 0
\]
D) Parabolün Oy eksenini kestiği nokta
\[(0, c) \quad \text{ve } c < 0 \]
E) \( a < 0, b > 0 \) ve \( c < 0 \) olduğundan
\[
ab + c < 0
\]
\(\textbf{Cevab: E} \)
SORU 10
\( y = x^2 + 3mx + 2m^2 + 1 \) parabolü Ox eksenine, eksenin pozitif tarafında teğet ise bu parabolün Oy eksenini kestiği noktanın ordinatı nedir?
\[
\text{A) } 7 \quad
\text{B) } 8 \quad
\text{C) } 9\quad
\text{D) } 10 \quad
\text{E) } 11
\]
Çözüm:
Parabol Ox eksenine, eksenin pozitif tarafında teğet olduğuna göre,
\[
\Delta = 0
\]
ve tepe noktasının apsisi
\[
r > 0
\]
dır.
O halde,
\[
\Delta = (3m)^2 – 4 \cdot 1 \cdot (2m^2 + 1) = 0
\]
\[
\Rightarrow 9m^2 – 8m^2 – 4 = 0
\]
\[
\Rightarrow m^2 – 4 = 0
\]
\[
\Rightarrow m = \pm 2
\]
ve
\[
r = -\frac{3m}{2} > 0
\]
olması için
\[
m < 0
\]
olmalıdır.
Buradan,
\[
m = -2
\]
bulunur.
Bu parabolün Oy eksenini kestiği noktanın ordinatı ise
\[
c = 2m^2 + 1
\]
\[
\Rightarrow c = 2 \cdot (-2)^2 + 1 = 9
\]
\(\textbf{Cevab: C} \)
SORU 11
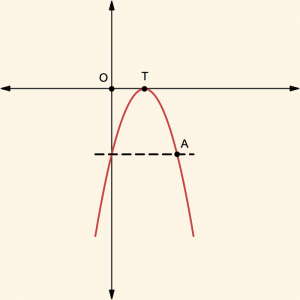
Verilen şekilde T tepe noktası Ox ekseni üzerinde olan
\[y = -x^2 – mx + 2m + 4\]
parabolü verilmiştir. A noktasının apsisi nedir?
\[
\text{A) } 1 \quad\text{B) } 2 \quad
\text{C) } 3\quad
\text{D) } 4 \quad
\text{E) } 5\]
Çözüm:
Parabol Ox eksenine teğet olduğundan,
\[\Delta = (-m)^2 – 4 \cdot (-1) \cdot (2m + 4) = 0\]
\[\Rightarrow (m+ 4)^2 = 0\]
\[\Rightarrow m = -4\]
değeri parabolün denkleminde yerine yazılırsa,
\[
y = -x^2 – mx + 2m + 4
\]
\[
\Rightarrow y = -x^2 + 4x – 4
\]
\[\Rightarrow y = -(x – 2)^2\]
olur. Parabolün tepe noktası
\[T(2, 0)\]
\[x = 2\]
doğrusu simetri eksenidir. O halde A noktasının apsisi 4 bulunur.
\(\textbf{Cevab: D} \)
SORU 12
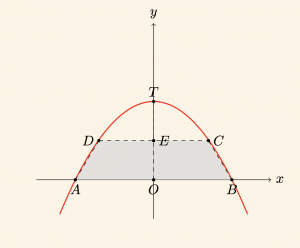
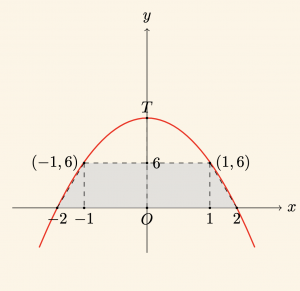
Yularıdaki şekilde T tepe noktası Oy ekseni üzerinde olan
\[
y = mx^2 – (m^2 – 4)x + 8
\]
parabolü verilmiştir. E noktasının ordinatı 6 olduğuna göre, ABCD yamuğunun alanı kaç birim karedir?
\[
\text{A) } 18 \quad
\text{B) } 16 \quad
\text{C) } 14\quad
\text{D) } 12 \quad
\text{E) } 10
\]
Çözüm:
Parabolün tepe noktası Oy ekseni üzerinde olduğundan,
\[
b = – (m^2 – 4) = 0 \Rightarrow m = 2 \text{ veya } m = -2
\]
Burada \( a = m < 0 \Rightarrow m = -2 \) olduğundan, denklem yerine yazılırsa,
\[
y = mx^2 – (m^2 – 4)x + 8 \Rightarrow y = -2x^2 + 8
\]
bulunur. C ve D noktaları parabol üzerinde olduğundan, bu noktaların apsisleri şu şekilde hesaplanır:
\[
y = 6 = -2x^2 + 8 \Rightarrow x = -1 \text{ , } x = 1
\]
Parabolün Ox eksenini kestiği noktalar:
\[
y = -2x^2 + 8 = 0 \Rightarrow x = -2 \text{ veya } x = 2
\]
olduğundan kesim noktaları (-2,0) ve (2,0) bulunur. Buna göre,
– \(|AB| = 4\) birim
– \(|DC| = 2\) birim
– \(|DE| = 6\) birim
olup, yamuk alanı şu şekilde hesaplanır:
\[
A(ABCD) = \frac{(4+2) \cdot 6}{2} = 18
\]
birim karedir.
\(\textbf{Cevab: A} \)