Bir Parabolle Bir Doğrunun Birbirine Göre Durumu
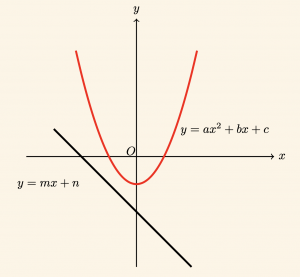
Denklemi \( y = ax^2 + bx + c \) olan bir parabolle, denklemi \( y = mx + n \) olan bir doğrunun birbirine göre durumunu incelemek için bu denklemler ortak çözülür.
\[
\left.
\begin{array}{l}
y= ax^2 + bx + c \\
y = mx+n\\
\end{array}
\right\} \quad \Rightarrow ax^2 + bx + c = mx+n \\
\\
\\
\]
\[\Rightarrow ax^2 + (b – m)x + (c – n) = 0 \]
şeklinde ikinci dereceden bir denklem elde edilir. Bu denklemde:
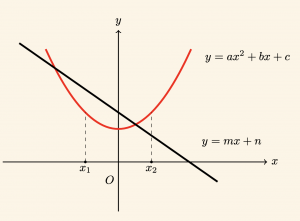
1) \( \quad \Delta > 0 \) ise,
Parabol ile doğru farklı iki noktada kesişir.
\( ax^2 + (b – m)x + c – n = 0 \) denkleminin kökleri olan \( x_1 \) ile \( x_2 \), bu iki kesim noktalarının apsisleridir.
Örnek:
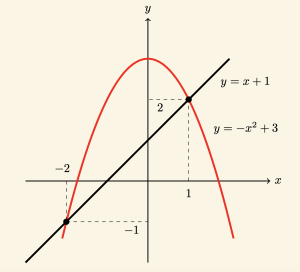
\( y = -x^2 + 3 \) parabolü ile \( y = x + 1 \) doğrusunun birbirine göre durumunu inceleyelim.
\[
\left.
\begin{aligned}
y &= -x^2 + 3 \\
y &= x + 1
\end{aligned}
\right\} \Rightarrow -x^2 + 3 = x + 1\]
\[\Rightarrow x^2 + x \; – 2 = 0\]
\[\Rightarrow x_1 = -2 \quad \text{ veya } \quad x_2 = 1 \]
olduğundan parabol ile doğru farklı iki noktada kesişir. Bulunan kökler, parabol veya doğrunun denkleminde yerine yazılarak kesim noktalarının ordinatları bulunur.
\[ y = x + 1 \;\; \text{de} \]
\[x_1 = -2 \quad \text{için} \quad y_1 = -1 \]
\[x_2 = 1 \quad \text{için} \quad y_2 = 2 \quad \text{bulunur} \]
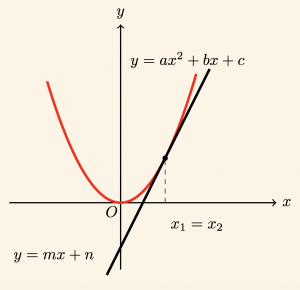
2) \( \quad \Delta = 0 \) ise,
Doğru, parabole teğettir. \( ax^2 + (b \;-\; m)x + c\; – \;n = 0 \) denkleminin iki kat kökü (\( x_1 = x_2 \)), doğrunun parabole teğet olduğu noktanın apsisidir.
Örnek:
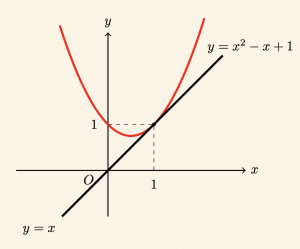
\( y = x^2 – x + 1 \) parabolü ile \( y = x \) doğrusunun birbirine göre durumunu inceleyelim.
\[
\left.
\begin{aligned}
y &= x^2 – x + 1 \\
y &= x
\end{aligned}
\right\}
\Rightarrow x^2 – x + 1 = x\]
\[\Rightarrow x^2 – 2x + 1 = 0
\Rightarrow x_1 = x_2 = 1 \]
olduğundan doğru, parabole teğettir. Bu noktanın ordinatını bulalım.
\[ y = x \quad \text{de} \quad x = 1 \quad \text{için} \quad y = 1 \quad \text{dir.} \]
3) \( \quad \Delta < 0 \) ise,
Parabol ile doğrunun ortak noktası yoktur.
Örnek:
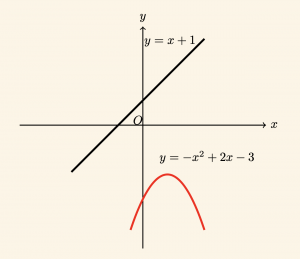
\( y = -x^2 + 2x – 3 \) parabolü ile \( y = x + 1 \) doğrusunun birbirine göre durumunu inceleyelim.
\[
\left.
\begin{aligned}
y &= -x^2 + 2x – 3 \\
y &= x + 1
\end{aligned}
\right\}
\Rightarrow -x^2 + 2x – 3 = x + 1\\ \]
\[
\Rightarrow x^2 – x + 4 = 0\\
\Rightarrow \Delta = -15 < 0
\]
olduğundan parabol ile doğrunun ortak noktası yoktur.
← Önceki Sayfa | Sonraki Sayfa →