\( x= f(y)= Ay^2+ By +C \) Parabolü
\( x = Ay^2 + By + C \) parabolü,
\( y = ax^2 + bx + c \) parabolüne benzer şekilde incelenir.
\[
\text{Tepe noktasının ordinatı: } \frac{-B}{2A}
\]
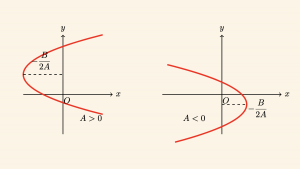
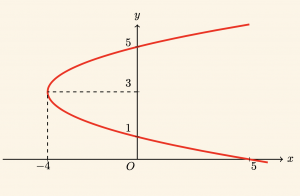
Örnek:
\( x = f(y) = y^2 – 6y + 5 \) parabolünü çizelim.
Parabolün tepe noktasının ordinatı:
\[
\frac{-(-6)}{2 \cdot 1} = 3
\]
ve apsisi:
\[
f(3) = 3^2 – 6 \cdot 3 + 5 = 9 – 18 + 5 = -4 \text{ tür.}
\]
Parabolün eksenleri kesim noktalarını bulalım.
\[
x = 0 \quad \text{ için } \quad y^2 – 6y + 5 = 0
\Rightarrow \quad y = 1 \quad \text{ veya } \quad y = 5
\]
\[
y = 0 \quad \text{ için } \quad x = 0^2 – 6 \cdot 0 + 5 = 5 \quad \text{ tir.}
\]
Ayrıca \( A = 1 > 0 \) olduğundan, parabolün kolları Ox ekseninin pozitif yönündedir.
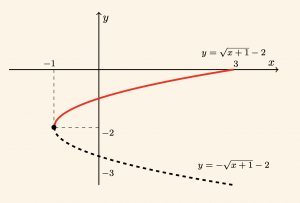
Örnek:
\[ y = \sqrt{x + 1} \;- \;2 \] eğrisini çizelim.
Eğrinin denklemi düzenlenirse,
\[ y = \sqrt{x + 1} – 2 \Rightarrow (y + 2)^2 = x + 1 \]
\[\Rightarrow x = (y + 2)^2 – 1 \text{ olur.} \]
Parabolün tepe noktası \( (-1, -2) \) ‘dir.
Eksenleri kesim noktalarını bulalım.
\[
x = 0 \quad \text{ için } \quad (y + 2)^2 – 1 = 0 \]
\[ \Rightarrow y = -1 \quad \text{ veya } \quad y = -3
\]
\[
y = 0 \quad \text{ için } \quad x = 3 \text{ tür.}
\]
Burada \( y = \sqrt{x + 1}\; – \;2 \) nin tanımlı olduğu
\[
x + 1 \geq 0 \Rightarrow x \geq -1 \quad \text{ve} \quad y \geq -2
\]
için grafiği çizelim.
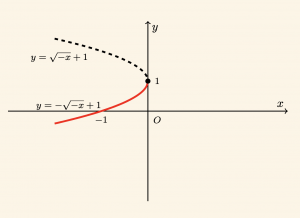
Örnek:
\( y = -\sqrt{-x } +1\) eğrisini çizelim.
Eğrinin denklemi düzenlenirse,
\[y = -\sqrt{-x } +1 \Rightarrow (y \;- \;1)^2 = (-\; \sqrt{-x})^2 \]
\[\Rightarrow x = – (y \;-\; 1)^2 \quad \text{ olur.}\]
Parabolün tepe noktası \( (0, 1) \) ve Ox eksenini kesim noktası,
\[
y = 0 \quad \text{ için } \quad x = -1 \quad \text{ olduğundan } \quad (-1, 0) \quad \text{ bulunur.}
\]
\( A = -1 < 0 \) olduğundan parabolün kolları Ox ekseninin negatif tarafındadır.
Burada \( y = -\sqrt{-x }+1 \) nin tanımlı olduğu
\[
-x \geq 0 \Rightarrow x \leq 0 \quad \text{ve} \quad y \leq 1
\]
için grafiği çizelim.
SORU 22
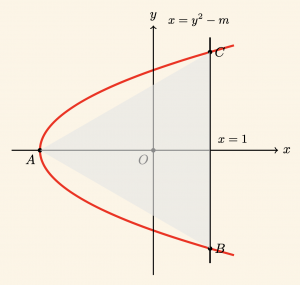
Yukarıdaki şekilde \( x = y^2 – m \) parabolü, \( x = 1 \) doğrusu ile B ve C noktalarında kesişiyorlar. ABC üçgeni eşkenar olduğuna göre, \( m \) kaçtır?
\[
\text{A)} 4 \sqrt{ 3} \quad
\text{B) } 2 \sqrt{ 3} \quad
\text{C) } \sqrt{ 3} \quad
\text{D) } 3 \quad
\text{E) } 2
\]
Çözüm:
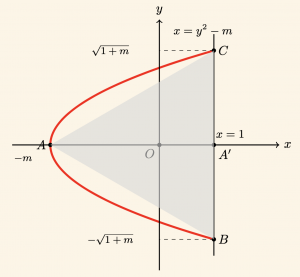
\( x = y^2 -\; m \) denkleminde \[ y = 0 \quad \text{için} \quad x = -m \quad \text{olduğundan} \quad A(-m, 0) \]
\( x = 1 \) için
\[
1 = y^2 – m \Rightarrow y = \pm\sqrt{1 + m}
\]
\[
B (1, -\sqrt{1 + m}) \quad \text{ve } \quad C = (1, \sqrt{1 + m})
\]
O halde
\[
|BC| = 2\sqrt{1 + m}, \quad |AA’| = 1 + m
\]
ve ABC üçgeni eşkenar olduğundan,
\[\frac{|BC| \cdot \sqrt{3}}{2} = |AA’| \]
\[\Rightarrow \frac{2\sqrt{1 + m} \cdot \sqrt{3}}{2} = 1 + m \]
\[\Rightarrow (\sqrt{1 + m} \cdot \sqrt{3})^2 = (1 + m)^2 \]
\[\Rightarrow 3(1 + m) = (1 + m)^2\]
\[
\Rightarrow (1 + m)(m – 2) = 0
\Rightarrow m = -1 \text{ veya } m = 2
\]
\( m > 0 \) verildiğinden \( m \ne -1 \), o halde
\[
m = 2 \text{ dir.}
\]
\(\textbf{Cevab: E} \)
SORU 23
Yandaki şekilde \( y = x + b \) doğrusu ile \( x = y^2 + 2y + a \) parabolü A ve B noktalarında kesişiyorlar. A noktası ile B noktasının ordinatları toplamı nedir?
\[
\text{A)} -3 \quad
\text{B) } -2\quad
\text{C) } -1\quad
\text{D) } 0 \quad
\text{E) } 1
\]
Çözüm:
Doğrunun denklemi ile parabolün denklemini ortak çözelim:
\[
\left.
\begin{aligned}
y &= x + b \\
x &= y^2 + 2y + a
\end{aligned}
\right \}
\Rightarrow y – b = y^2 + 2y + a\]
\[\Rightarrow y^2 + y + a + b = 0\]
İkinci dereceden denklemin kökler toplamı:
\[
y_1 + y_2 = -1 \text{ dir.}
\]
\(\textbf{Cevab: C} \)
← Önceki Sayfa | Sonraki Sayfa →