Eşitsizlikler

 

Eşitsizlikler

 

Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler:

 

\( a, b \in \mathbb{R} \) ve \( a \ne 0 \) olmak üzere,

\[ ax + b > 0 \] \[ax + b \ge 0 \]\[ax + b < 0 \] veya \[ ax + b \le 0 \]

şeklindeki eşitsizliklere birinci dereceden bir bilinmeyenli eşitsizlikler denir. Eşitsizliği sağlayan \( x \) reel sayılarının kümesine eşitsizliğin çözüm kümesi denir.

Birinci dereceden bir bilinmeyenli bir eşitsizliği çözmek demek, \( f(x) = ax + b \) iki terimlisinin işaretini inceleyerek eşitsizliği sağlayan aralığı bulmak demektir.

\[ f(x) = ax + b \]

nin grafiğini çizerek işaretini inceleyelim.

 

1) \( \quad   a > 0 \) olmak üzere,

\[x > -\frac{b}{a} \quad   \text{ için } \quad   f(x) > 0, \]
\[x < -\frac{b}{a}  \quad  \text{ için } \quad   f(x) < 0 \text{ dır.} \]

 

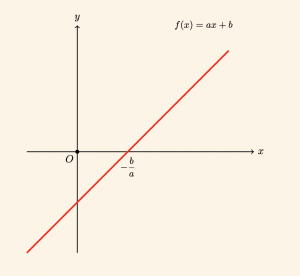
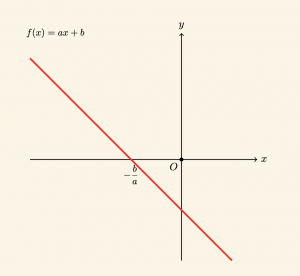
2) \( \quad   a < 0 \) olmak üzere,

\[x > -\frac{b}{a} \quad   \text{ için } \quad   f(x) < 0, \quad \]
\[x < -\frac{b}{a} \quad   \text{ için } \quad   f(x) > 0 \text{ dır.} \]

Buna göre,

\[
x > -\frac{b}{a} \quad   \text{ için } \quad   ax + b \quad   \text{ nin işareti }\;\; a \text{ nın işaretinin aynısı,}
\]
\[
x < -\frac{b}{a} \quad   \text{ için } \quad   ax + b \quad   \text{ nin işareti }\;\; a \text{ nın işaretinin tersidir.}
\]

Bu durumu tabloda gösterelim:

 

Örnek:

\[
\\
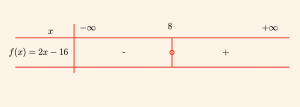
f(x) = 2x – 16 \text{ iki terimlisinin işaretini inceleyelim.} \]
\[2x – 16 = 0 \Rightarrow x = 8 \quad \text{ve} \quad a = 2 > 0 \text{ olduğundan,}
\]

\[
\begin{aligned}
x > 8 &\Rightarrow 2x – 16 > 0 \\
x < 8 &\Rightarrow 2x – 16 < 0
\end{aligned}
\]

 

Örnek:

\[
\\
f(x) = 4-2x \;\;  \text{ iki terimlisinin işaretini inceleyelim.} \]
\[4- 2x = 0 \Rightarrow x = 2 \quad \text {ve} \quad a = -2 < 0 \text{ olduğundan,} \]

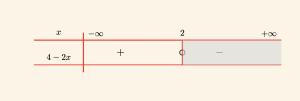
\[ Ç= \{ x | -\infty < x ≤ 2, x \in \mathbb{R} \} \]