İkinci Dereceden İki Bilinmeyenli Bir Denklemin Köklerinin İşaretinin İncelenmesi
\(f(x) = ax^2 + bx + c\) ikinci dereceden fonksiyonunun grafiğinden (parabol) faydalanarak
\(ax^2 + bx + c = 0\) denkleminin köklerinin varlığını ve işaretini belirleyebiliriz.
\( 1. \quad \) \(\Delta = b^2 – 4ac < 0\)
\(b^2-4ac < 0 \) ise denklemin reel kökleri olmadığından, köklerinin işareti de söz konusu değildir.
\( 2. \quad \) \(\Delta = b^2 – 4ac = 0\)
ise denklemin birbirine eşit reel iki kökü vardır. Denklemin kökleri \(x_1\), \(x_2\) ve \(x_1 = x_2\) olsun.
a) \(x_1 + x_2 < 0 \Leftrightarrow x_1 = x_2 < 0\)
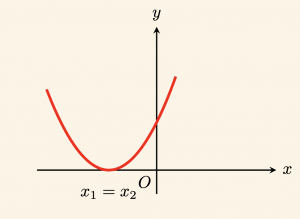
birbirine eşit negatif iki kök vardır.
b) \(x_1 + x_2 = 0 \Leftrightarrow x_1 = x_2 = 0\)
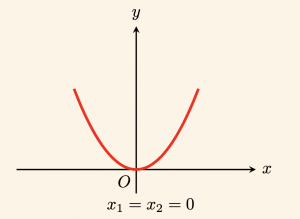
denklemin kökleri orjindedir.
c) \(x_1 + x_2 > 0 \Leftrightarrow x_1 = x_2 > 0\)
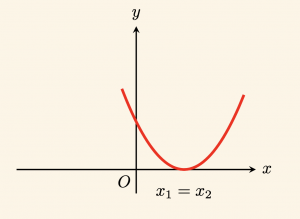
birbirine eşit pozitif iki kök vardır.
\( 3. \quad \) \(\Delta = b^2 – 4ac > 0\)
ise denklemin birbirinden farklı reel iki kökü vardır. Denklemin kökleri \(x_1\), \(x_2\) ve \(x_1 < x_2\) olsun.
a)
\[
\left.
\begin{aligned}
x_1 \cdot x_2 > 0 \\
x_1 + x_2 > 0
\end{aligned}
\right\} \Leftrightarrow 0 < x_1 < x_2 \\
\]
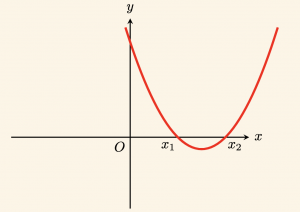
Pozitif iki kök vardır.
b)
\[
\left.
\begin{aligned}
x_1 \cdot x_2 > 0 \\
x_1 + x_2 < 0
\end{aligned}
\right\} \Leftrightarrow x_1 < x_2 < 0 \\
\]
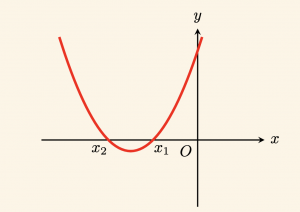
Negatif iki kök vardır.
c)
\[
\left.
\begin{aligned}
x_1 \cdot x_2 < 0 \\
x_1 + x_2 > 0
\end{aligned}
\right\} \Leftrightarrow x_1 < 0 < x_2 \text{ ve } |x_1| < x_2 \\
\]
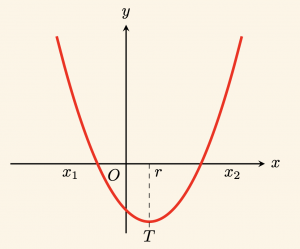
Mutlak değerce büyük olan kök pozitiftir. Ters işaretli iki kök vardır.
d)
\[
\left.
\begin{aligned}
x_1 \cdot x_2 < 0 \\
x_1 + x_2 < 0
\end{aligned}
\right\} \Leftrightarrow x_1 < 0 < x_2 \text{ ve } |x_1| > x_2 \\
\]
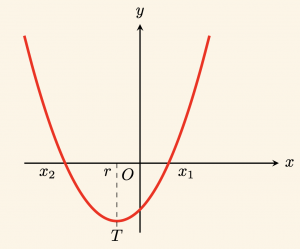
Mutlak değerce büyük olan kök negatiftir. Ters işaretli iki kök vardır.
e)
\[\left.
\begin{aligned}
x_1 \cdot x_2 < 0 \\
x_1 + x_2 = 0
\end{aligned}
\right\}
\Leftrightarrow x_1 < 0 < x_2 \text{ ve } \quad |x_1| = x_2 \]

Mutlak değerce eşit, ters işaretli iki kök vardır.
f)
\[\left.
\begin{aligned}
x_1 \cdot x_2 = 0 \\
x_1 + x_2 > 0
\end{aligned}
\right\}
\Leftrightarrow x_1 = 0 < x_2 \]
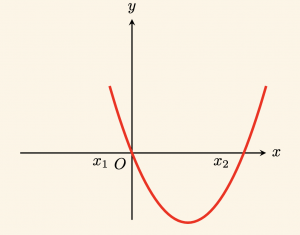
Biri sıfır, diğeri pozitif olan iki kök vardır.
g)
\[ \left.
\begin{aligned}
x_1 \cdot x_2 = 0 \\
x_1 + x_2 < 0
\end{aligned}
\right\}
\Leftrightarrow x_1 < 0 = x_2 \]
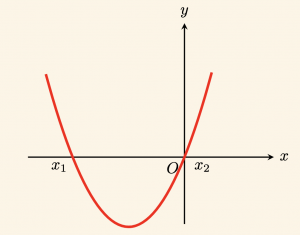
Biri sıfır, diğeri negatif olan iki kök vardır.
Örnek:
\(x^2 – (m^2 + 1)x\; – m^2 \;- 1 = 0\) denkleminin köklerinin varlığını ve işaretini inceleyelim.
\(a = 1 > 0\) ve \(c = -m^2\; – 1 < 0\) olduğundan \(\Delta > 0\)’dır. Denklemin farklı reel iki kökü vardır. Bu kökler \(x_1, \;\; x_2\) ve \(x_1\; <\; x_2\) olsun.
\[
\left.
\begin{aligned}
&x_1 \cdot x_2 = -m^2 – 1 < 0 \\
&x_1 + x_2 = m^2 + 1 > 0
\end{aligned}
\right\}
\text{ olduğundan } x_1 < 0 < x_2 \text{ ve } |x_1| < x_2 \text{ dir.}
\]
Örnek:
\(16x^2 -\; 1000x + 5^6 = 0\) denkleminin köklerinin varlığını ve işaretini inceleyelim.
\[
\Delta = (-1000)^2 – 4 \cdot 16 \cdot 5^6 = 10^6 – 2^6 \cdot 5^6 = 0
\]
olduğundan denklemin birbirine eşit iki kökü vardır. Bu kökler \(x_1, \; x_2\) olsun.
\[
x_1 + x_2 = -\frac{-1000}{16} = \frac{125}{2} > 0 \Rightarrow x_1 = x_2 > 0 \text{ dır.}
\]
SORU 29
\(mx^2 -\; 2(1 – \;m)x + m -\; 2 = 0\) denkleminin \(x_1,\; x_2\) kökleri arasında \(x_1 < 0 < x_2\) ve \(x_2 < |x_1|\) bağıntıları olduğuna göre, \(m\) için aşağıdakilerden hangisi doğrudur?
\[ \text{A) } m < 0\ \quad
\text{B) } 0 < m < 1\ \quad
\text{C) } 1 < m < 2 \quad
\text{D) }2 < m < 3 \quad
\text{E) } m > 3 \]
Çözüm:
Verilen denklem:
\[
mx^2 – 2(1 – m)x + m – 2 = 0
\]
\[x_1 < 0 < x_2 \Rightarrow x_1 \cdot x_2 = \frac{m – 2}{m} < 0\]
\(x_1 < 0\) olduğundan \(|x_1| = -x_1\) olur.
Ayrıca \(x_2 < |x_1| \Rightarrow x_2 < -x_1 \Rightarrow x_1 + x_2 < 0\)
\[
x_1 + x_2 = \frac{2(1 – m)}{m} < 0
\]
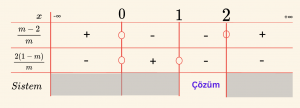
\[
Ç = \{ m \mid 1 < m < 2,\ m \in \mathbb{R} \} \text{ dir.}
\]
\(\textbf{Cevab: C} \)
← Önceki Sayfa | Sonraki Sayfa →