Esas Ölçü

 

Esas Ölçü

 

\( \alpha \in [0, 2\pi) \) olmak üzere,

Yukarıda görüldü ki, \( \alpha + 2k\pi \) radyanlık açının bitim kenarı ile \( \alpha \) radyanlık açının bitim kenarı birim çemberi aynı (P) noktada kesiyor. Yani bu açıların birim çember üzerinde gösterdiği noktalar aynıdır. Burada \( \alpha \) radyanlık açıya \( \alpha + 2k\pi \) radyanlık açının esas ölçüsü denir.

Örneğin

 

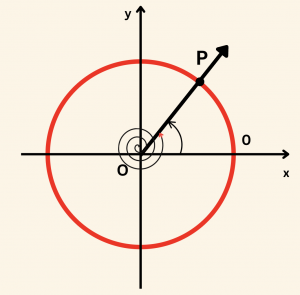
\( k = 2 \) seçilirse A noktasından pozitif yönde iki defa \( 2\pi \) radyanlık yay çizildiğinde tekrar A noktasına gelinir.

\( \alpha + 4\pi \) radyandan \( 4\pi \) radyan çıkarılırsa elde edilen \( \alpha \) radyanlık açı ile \( \alpha + 4\pi \) radyanlık açının birim çember üzerinde gösterdiği noktalar aynıdır.

O halde \( \alpha \) radyanlık açı, \( \alpha + 4\pi \) radyanlık açının esas ölçüsüdür.

 

 

 

Sonuç:

Ölçüsü \( A^\circ \) olan bir açının esas ölçüsü \( a^\circ \) ve \( a \in [0, 360) \) ise,

\[
A \equiv a \pmod{360} \;\; \text{dir.}
\]

Ölçüsü \( B \) radyan olan bir açının esas ölçüsü \( b \) radyan ve \( b \in [0, 2\pi) \) ise,

\[
B \equiv b \pmod{2\pi} \;\; \text{dir. }
\]

Ölçüsü \( C \) grad olan bir açının esas ölçüsü \( c \) grad ve \( c \in [0, 400) \) ise,

\[
C \equiv c \pmod{400} \;\; \text{dür. }
\]

Sonuç olarak,

Ölçüsü derece cinsinden verilen bir açının esas ölçüsünü bulmak için bu açının ölçüsü 360’a bölünür. Kalan esas ölçüdür.

Ölçüsü radyan cinsinden verilen bir açının esas ölçüsünü bulmak için bu açının ölçüsünden \( 2\pi \)’nin tam katları atılır. Kalan esas ölçüdür.

Ölçüsü grad cinsinden verilen bir açının esas ölçüsünü bulmak için bu açının ölçüsü 400’e bölünür. Kalan esas ölçüdür.

 

Örnekler:

1200°, -1200°, 19000° ve -19000°’lik açıların esas ölçüsünü bulalım.

\(\bullet   \)  1200° açının esas ölçüsü

\[
\begin{array}{r|l}
1200  & 360 \\
1080  & \rule{10mm}{0.30mm} \\
–  \rule{15mm}{0.30mm} & 3\\
120&
\end{array}
\]

1200°’lik açının esas ölçüsü \( 120^\circ \)’dir.

\(\bullet   \)  -1200° açının esas ölçüsü

\[
\begin{array}{r|l}
-1200  & 360 \\
-1440  & \rule{10mm}{0.30mm} \\
–  \rule{15mm}{0.30mm} & -4\\
240&
\end{array}
\]

-1200°’lik açının esas ölçüsü \( 240^\circ \)’dir.

 

\(\bullet   \)  19000° açının esas ölçüsü

\[
\begin{array}{r|l}
19000  & 360 \\
18720  & \rule{10mm}{0.30mm} \\
–  \rule{15mm}{0.30mm} & 52\\
280&
\end{array}
\]

19000°’lik açının esas ölçüsü \( 280^\circ \)’dir.

 

\(\bullet   \)  -19000° açının esas ölçüsü

\[
\begin{array}{r|l}
-19000  & 360 \\
-19080  & \rule{10mm}{0.30mm} \\
–  \rule{15mm}{0.30mm} & -53\\
80&
\end{array}
\]

-19000°’lik açının esas ölçüsü \( 80^\circ \)’dir.

 

Örnekler:

\( \frac{45\pi}{4} \) radyanlık açı ile \( -\frac{45\pi}{4} \) radyanlık açının esas ölçüsünü bulalım.

\[
\frac{45\pi}{4} = \frac{40\pi + 5\pi}{4} = 10\pi + \frac{5\pi}{4}
\]

olur. \( 10\pi \) atılırsa \( \frac{45\pi}{4} \) radyanlık açının esas ölçüsü

\[
\frac{5\pi}{4}
\]

radyan olarak bulunur. Burada,

\[
\frac{45\pi}{4} = \frac{44\pi + \pi}{4} = 11\pi + \frac{\pi}{4}
\]

olur. Fakat \( 11\pi \) atılırsa esas ölçü bulunmuş olmaz. Çünkü \( 11\pi \), \( 2\pi \)’nin tam katı değildir.

\[
\begin{array}{r|l}
-45 \pi  & 4 \\
-48 \pi  & \rule{10mm}{0.30mm} \\
–  \rule{15mm}{0.30mm} & -12 \pi  \\
3 \pi  &
\end{array}
\]

olur. \( -12\pi \) atılırsa

\[
-\frac{45\pi}{4} \text{ radyanlık açının esas ölçüsü } \frac{3\pi}{4} \text{ radyan olarak bulunur.}
\]

Örnek:

7777 gradlık bir açının esas ölçüsünü bulalım.

\[
\begin{array}{r|l}
7777  & 400 \\
7600  & \rule{10mm}{0.30mm} \\
–  \rule{15mm}{0.30mm} & 19\\
177&
\end{array}
\]