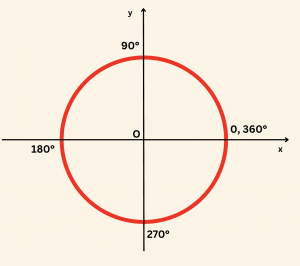
90° \( ( \pi/2 \;\; Radyan) \) den Büyük Açıların Trigonometrik Oranları
Trigonometrik Oranları:
\(\theta\), 90°’den büyük bir açı olsun. \(\theta\)’nın herhangi bir trigonometrik oranını bulmak için bu açı 0°, 90°, 180°, 270° veya 360° ile bir \(\alpha\) açısının toplamı veya farkı şeklinde yazılır. \(\alpha\) dar açı kabul edilerek toplam veya fark
\[(0° − \alpha , \quad 90° + \alpha, \quad 180° ± \alpha , \quad 270° ± \alpha , \quad 360° − \alpha ) \]
şeklinde yazılan açının aranan trigonometrik oranının işareti tespit edilir. Daha sonra elde edilecek yeni trigonometrik oran \(\alpha\) cinsinden aşağıdaki gibi bulunur.
1) \(\theta\) açısı (0° − \(\alpha\)), (180° ± \(\alpha\)) veya (360° − \(\alpha\)) şeklinde yazılırsa trigonometrik oran değişmez.
2) \(\theta\) açısı (90° ± \(\alpha\)) veya (270° ± \(\alpha\)) şeklinde yazılırsa trigonometrik oran ko-fonksiyonuna (sin ↔ cos, tan ↔ cot, sec ↔ csc) dönüşür.
Örnek:
\(\cos 240^\circ\) trigonometrik değerinin eşitini bulalım.
\[240^\circ = 270^\circ – 30^\circ\] şeklinde yazılırsa
\(\cos(270^\circ – 30^\circ) < 0\) dır. ( \( \cos \) fonksiyonu ikinci bölgede (-) dir. )
Ayrıca trigonometrik oran ko-fonksiyonuna (cos → sin) dönüşür. O halde,
\[\cos 240^\circ = \cos(270^\circ – 30^\circ) = -\sin 30^\circ\] bulunur.
Örnek:
\(\cos(2\pi – \alpha)\) trigonometrik değerinin eşitini bulalım.
\(\alpha\) dar açı kabul edileceğinden,
\[\frac{3\pi}{2} < 2\pi – \alpha < 2\pi\] olur.
Buna göre \(\cos(2\pi- \alpha) > 0\) dır. Ayrıca trigonometrik oran değişmez. O halde,
\[\cos(2\pi – \alpha) = \cos \alpha\] bulunur.
Örnekler:
\( \bullet \quad \sin 135^\circ = \sin(90^\circ + 45^\circ) = \cos 45^\circ = \frac{\sqrt{2}}{2}\)
\( \bullet \quad \tan \frac{7\pi}{4} = \tan\left(\frac{3\pi}{2} + \frac{\pi}{4}\right) = -\cot \frac{\pi}{4} = -1\)
\( \bullet \quad \cot \frac{11\pi}{6} = \cot\left(2\pi – \frac{\pi}{6}\right) = -\cot \frac{\pi}{6} = -\sqrt{3}\)
\( \bullet \quad \sec(\pi – \alpha) = -\sec \alpha\)
\( \bullet \quad \csc\left(\frac{\pi}{2} + \alpha\right) = \sec \alpha\)
\( \bullet \quad \tan(19\pi + \alpha) = \tan(18\pi + \pi + \alpha) = \tan(\pi + \alpha) = \tan \alpha\)
\(\bullet \quad \cos(1996\pi – \alpha) = \cos(0 – \alpha) = \cos \alpha\)
\[
\begin{array}{| l | r | }
\hline
\sin\left(\frac{\pi}{2} – \theta\right) = \cos \theta \quad \quad \quad &\sin\left(\frac{\pi}{2} + \theta\right) = \cos \theta \\
\hline
\cos\left(\frac{\pi}{2} – \theta\right) = \sin \theta \quad &\cos\left(\frac{\pi}{2} + \theta\right) = -\sin \theta \\
\hline
\tan\left(\frac{\pi}{2} – \theta\right) = \cot \theta \quad &\tan\left(\frac{\pi}{2} + \theta\right) = -\cot \theta \\
\hline
\cot\left(\frac{\pi}{2} – \theta\right) = \tan \theta \quad &\cot\left(\frac{\pi}{2} + \theta\right) = -\tan \theta \\
\hline
\end{array}
\]
\[
\begin{array}{| l | r | }
\hline
\sin(\pi – \theta) = \sin \theta \quad \quad \quad & \sin(\pi + \theta) = -\sin \theta \\
\hline
\cos(\pi – \theta) = -\cos \theta\quad \quad \quad & \cos(\pi + \theta) = -\cos \theta \\
\hline
\tan(\pi – \theta) = -\tan \theta \quad \quad \quad & \tan(\pi + \theta) = \tan \theta \\
\hline
\cot(\pi – \theta) = -\cot \theta \quad \quad \quad & \cot(\pi + \theta) = \cot \theta \\
\hline
\end{array}
\]
\[
\begin{array}{| l | r | }
\hline
\sin\left(\frac{3\pi}{2} – \theta\right) = -\cos \theta \quad \quad & \sin\left(\frac{3\pi}{2} + \theta\right) = -\cos \theta \\
\hline
\cos\left(\frac{3\pi}{2} – \theta\right) = -\sin \theta \quad \quad & \cos\left(\frac{3\pi}{2} + \theta\right) = \sin \theta \\
\hline
\tan\left(\frac{3\pi}{2} – \theta\right) = \cot \theta \quad \quad & \tan\left(\frac{3\pi}{2} + \theta\right) = -\cot \theta \\
\hline
\cot\left(\frac{3\pi}{2} – \theta\right) = \tan \theta \quad \quad & \cot\left(\frac{3\pi}{2} + \theta\right) = -\tan \theta \\
\hline
\end{array}
\]
\[
\begin{array}{| l | r | }
\hline
\sin(2\pi – \theta) = -\sin \theta \quad \quad \quad & \sin(-\theta) = -\sin \theta \\
\hline
\cos(2\pi – \theta) = \cos \theta \quad \quad \quad & \cos(-\theta) = \cos \theta \\
\hline
\tan(2\pi – \theta) = -\tan \theta\quad \quad \quad & \tan(-\theta) = -\tan \theta \\
\hline
\cot(2\pi – \theta) = -\cot \theta \quad \quad \quad & \cot(-\theta) = -\cot \theta \\
\hline
\end{array}
\]
SORU 30
\(\sin 7^\circ = a\) ise
\[
\frac{\sin 277^\circ \cdot \tan 173^\circ}{\cos 353^\circ \cdot \cos 97^\circ}
\]
aşağıdakilerden hangisine eşittir?
\[
\text{A) } 1 \quad
\text{B) } \frac{1}{a} \quad
\text{C) } -\frac{1}{a} \quad
\text{D) } \frac{1}{\sqrt{1 – a^2}} \quad
\text{E) } \frac{-1}{\sqrt{1 – a^2}}
\]
Çözüm:
\[
\frac{\sin 277^\circ \cdot \tan 173^\circ}{\cos 353^\circ \cdot \cos 97^\circ} =
\frac{\sin(270^\circ + 7^\circ) \cdot \tan(180^\circ – 7^\circ)}{\cos(360^\circ – 7^\circ) \cdot \cos(90^\circ + 7^\circ)}
\]
\[
= \frac{-\cos 7^\circ \cdot (-\tan 7^\circ)}{\cos 7^\circ \cdot (-\sin 7^\circ)} =
\frac{-1}{\cos 7^\circ}
\]
\[
= \frac{-1}{\sqrt{1 – \sin^2 7^\circ}} = \frac{-1}{\sqrt{1 – a^2}}
\]
\(\textbf{Cevab: E} \)
SORU 31
\[
\frac{\cos 3799^\circ}{\cos 3851^\circ}\; -\; \tan 71^\circ
\]
işleminin sonucu nedir?
\[
\text{A) } 2 \tan 19^\circ \quad
\text{B) } – \tan 71^\circ \quad
\text{C) } -2 \cot 19^\circ \quad
\text{D) } \cot 19^\circ \quad
\text{E) } 0
\]
Çözüm:
\[
\frac{\cos 3799^\circ}{\cos 3851^\circ}\; – \;\tan 71^\circ
\]
\[
= \frac{\cos(10 \cdot 360^\circ + 199^\circ)}{\cos(10 \cdot 360^\circ + 251^\circ)}\; -\; \tan 71^\circ
= \frac{\cos 199^\circ}{\cos 251^\circ } \; -\; \tan 71
\]
\[
= \frac{\cos(180^\circ + 19^\circ)}{\cos(270^\circ \;-\; 19^\circ)}- \cot 19^\circ
\]
\[= \frac{-\cos 19^\circ}{- \sin 19^\circ} \;-\; \cot 19^\circ \]
\[ = \frac{-\cos 19^\circ }{- \sin 19} \;-\; \cot 19^\circ \]
\[= \cot 19^\circ- \cot 19^\circ =0 \]
\(\textbf{Cevab: E} \)
Uyarı:
\[
\begin{aligned}
\cos(-\theta) &= \cos(0\; -\; \theta) = \cos \theta \\
\sin(-\theta) &= \sin(0\; – \;\theta) = -\sin \theta \\
\tan(-\theta) &= \tan(0\; -\; \theta) = -\tan \theta \\
\cot(-\theta) &= \cot(0 \;- \;\theta) = -\cot \theta \\
\end{aligned}
\]
SORU 32
\[
\frac{\sin(91\pi + \theta) + \sin(90\pi – \theta)}{\sin\left(-\frac{\pi}{2} – \theta\right) – \cos(-\theta)}
\]
ifadesi aşağıdakilerden hangisine eşittir?
\[
\text{A) } 1\quad
\text{B) } -\tan \theta\quad
\text{C) } -\cot \theta \quad
\text{D) } \tan \theta \quad
\text{E) } \cot \theta
\]
Çözüm:
\[
\frac{\sin(91\pi + \theta) + \sin(90\pi – \theta)}{\sin\left(-\frac{\pi}{2} – \theta\right) – \cos(-\theta)} =
\frac{\sin(90\pi + \pi + \theta) + \sin(0 – \theta)}{-\sin\left(\frac{\pi}{2} + \theta\right) – \cos \theta}
\]
\[
= \frac{-\sin \theta – \sin \theta}{- \cos \theta – \cos \theta} =
\frac{-2\sin \theta}{-2\cos \theta} = \tan \theta
\]
\(\textbf{Cevab: D} \)
SORU 33
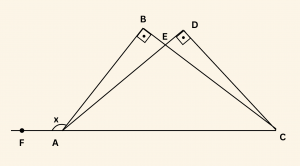Yandaki şekilde:
\(m(\hat B) = 90^\circ\)
\(m(\hat D) = 90^\circ\)
\(m(\hat{ FAD}) = x\)
\[
|BC| = 12 \text{ birim}, \quad |DC| = 8 \text{ birim}, \quad |AE| = |EC|
\]
olduğuna göre, \(\tan x\) nedir?
\[
\text{A) } -\frac{1}{3}\quad
\text{B) } -\frac{2}{3}\quad
\text{C) } -\frac{3}{4}\quad
\text{D) } -2 \quad
\text{E) } -3
\]
Çözüm:
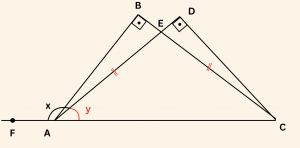
\(\triangle ABE \sim \triangle CDE \quad \) ve \( |AE| = |EC| \) olduğundan \( \triangle ABE \) ile \( \triangle CDE \) eş üçgenlerdir.
O halde
\[\begin{aligned} &|BE| = |ED| \\ + & |EC| = |AE| \\ \hline \\ &|BC| = |AD| = 12 \text{ dir.}\end{aligned}\]
\[\begin{aligned} m(\hat {CAD}) = y \quad \text{ denilirse } \quad x = 180^\circ – y \\
\tan x = \tan(180^\circ – y) = -\tan y \end{aligned}\]
\[
= -\frac{|DC|}{|AD|} = -\frac{8}{12} = -\frac{2}{3} \text{ tür.}
\]
\(\textbf{Cevab: B} \)
SORU 34
A, B ve C bir üçgenin açıları olduğuna göre,
\[
\frac{\tan(A + B) + \tan A}{\tan(B + C) + \tan C}
\]
ifadesi aşağıdakilerden hangisine eşittir?
\[
\text{A) } -1\quad
\text{B) } 1\quad
\text{C) } \frac{\tan A}{\tan B}\quad
\text{D) } -\frac{\tan A}{\tan B} \quad
\text{E) } \frac{\cot A}{\tan C}
\]
Çözüm:
A + B + C = \(180^\circ\) olduğundan,
\[
\frac{\tan(A + B) + \tan A}{\tan(B + C) + \tan C}
= \frac{\tan(180^\circ – C) + \tan A}{\tan(180^\circ – A) + \tan C}
\]
\[
= \frac{-\tan C + \tan A}{-\tan A + \tan C}
= -1 \quad \text{dir.}
\]
\(\textbf{Cevab: A} \)
SORU 35
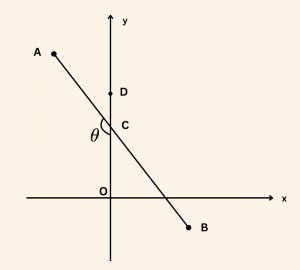
Yandaki şekilde \(A(-2, 7)\), \(B(3, -5)\) noktaları verilmiştir. \(m(\hat{ ACO}) = \theta\) olduğuna göre,
\(\sin \theta\) nın değeri nedir?
\[
\text{A) } \frac{1}{4}\quad
\text{B) } \frac{1}{3}\quad
\text{C) } \frac{5}{13}\quad
\text{D) } \frac{8}{13} \quad
\text{E) } \frac{12}{13}
\]
Çözüm:
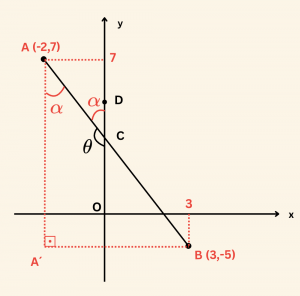
\(|AA’| = 12\) birim,
\(|A’B| = 5\) birim olduğundan \(AA’B\) dik üçgeninde Pisagor bağıntısından
\(|AB| = 13\) birimdir.
\(m(\hat {ACD}) = \alpha\) denilirse,
\(\theta = 180^\circ – \alpha\) ve
\(m(\hat A’AC) = \alpha\) olur. O halde \(AA’B\) dik üçgeninden,
\[
\sin \theta = \sin(180^\circ – \alpha) = \sin \alpha = \frac{|A’B|}{|AB|} = \frac{5}{13} \quad \text{tür.}
\]
\(\textbf{Cevab: C} \)
Uyarı:
90°’den büyük bir \(\theta\) açısının trigonometrik oranlarından herhangi birisi bilindiği zaman, bu açının diğer trigonometrik oranları dik üçgen yardımıyla bulunurken \(\theta\) dar açı kabul edilerek bilinen ve aranan trigonometrik oranın mutlak değeri alınmış olur.
SORU 36
\[
\pi < x < \frac{3\pi}{2}
\]
olmak üzere,
\[
3 \tan^2 x + 8 \tan x – 3 = 0
\]
ise \(\sin x\) in değeri nedir?
\[
\text{A) } -\frac{1}{\sqrt{10}} \quad
\text{B) } \frac{1}{\sqrt{10}} \quad
\text{C) } -\frac{1}{\sqrt{3}} \quad
\text{D) } \frac{1}{\sqrt{3}} \quad
\text{E) } \frac{1}{3}
\]
Çözüm:
\[
3 \tan^2 x + 8 \tan x – 3 = 0
\]
denkleminde \(\tan x = t\) denilirse,
\[
3t^2 + 8t – 3 = 0 \Rightarrow t = -3 \text{ veya } t = \frac{1}{3}
\]
\[
\pi < x < \frac{3\pi}{2}
\]
için \(\tan x > 0\) olduğundan,
\[
t = \tan x = \frac{1}{3} \text{ tür.}
\]
Buradan
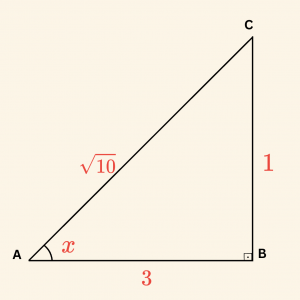x dar açı kabul edilerek yandaki dik üçgen yardımıyla
\[
|\sin x| = \frac{1}{\sqrt{10}} \quad \text{dur.}
\]
\[
\pi < x < \frac{3\pi}{2}
\]
için \(\sin x < 0\) olduğundan,
\[
-\sin x = \frac{1}{\sqrt{10}} \Rightarrow \sin x = -\frac{1}{\sqrt{10}} \quad \text{dur.}
\]
\(\textbf{Cevab: A} \)
SORU 37
\[
\frac{\pi}{2} < \theta < \pi \quad \text{ ve } \quad \tan \theta = -\frac{3}{4}
\]
olmak üzere,
\[
A = \cos(\pi + \theta) \cdot \tan\left(\frac{3\pi}{2} + \theta\right)
\]
ise \(A\) nın değeri nedir?
\[
\text{A) } \frac{4}{5} \quad
\text{B) } \frac{13}{15} \quad
\text{C) } \frac{14}{15} \quad
\text{D) } 1 \quad
\text{E) } \frac{16}{15}
\]
Çözüm:
\(\theta\) dar açı kabul edilirse,
\[\begin{aligned}A & = \cos(\pi + \theta) \cdot \tan\left(\frac{3\pi}{2} + \theta\right)\\ \\
&= -\cos \theta \cdot (-\cot \theta) \\ \\
&= \cos \theta \cdot \frac{1}{\tan \theta} \end{aligned}\]
Aşağıdaki dik üçgenden \(\cos \theta\) nın değerini bulalım.
\[
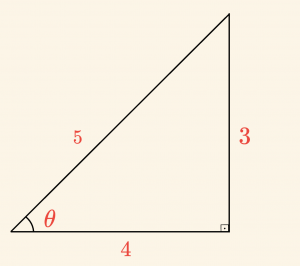
\tan \theta = -\frac{3}{4} \Rightarrow |\tan \theta| = \frac{3}{4}
\]
Buna göre yandaki dik üçgen çizilirse,
\[
|\cos \theta| = \frac{4}{5}
\]
\[
\frac{\pi}{2} < \theta < \pi \Rightarrow \cos \theta < 0
\]
\[
\Rightarrow \cos \theta = -\frac{4}{5}
\]
Buradan,
\[
A = -\frac{4}{5} \cdot \frac{1}{-\frac{3}{4}} = \frac{16}{15} \quad \text{tır.}
\]
\(\textbf{Cevab: E} \)