Sinüs Teoremi
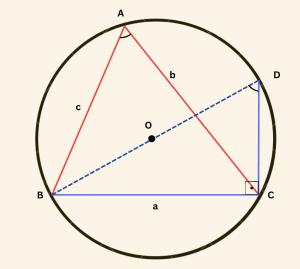Yandaki şekilde \(ABC\) üçgeninin çevrel çemberinin çapı \(|BD| = 2R\)’dir. \( m(\hat{ BAC}) =m (\hat{ BDC}) \) (aynı yayı gören çevre açılar)
\( BCD \) dik üçgeninde:
\[
\sin D = \frac{|BC|}{|BD|} \Rightarrow \sin A = \frac{a}{2R}
\]
\[
\Rightarrow \frac{a}{\sin A} = 2R \quad \text{elde edilir.}
\]
O halde genel formül yazılır:
\[
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R
\]
Bu eşitlik Sinüs Teoremi olarak bilinir.
Sonuç:
Bir üçgende kenar uzunlukları, karşılarındaki açıların sinüsleri ile orantılıdır. Bu oran üçgenin çevrel çemberinin çapının uzunluğuna eşittir.
Örnek:
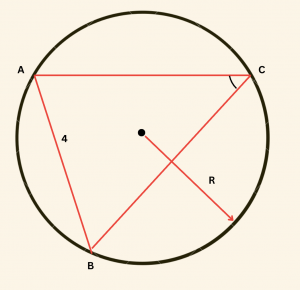
Yandaki şekilde \( O \) merkezli çemberin yarıçapının uzunluğu \( R = 4 \, \text{cm} \)’dir. \( |AB| = 4 \, \text{cm} \) olduğuna göre \( C \) dar açısının kaç derece olduğunu bulalım.
ABC üçgeninde sinüs teoremi yazılırsa,
\[ \frac{|AB|}{\sin C} = 2R \Rightarrow \frac{4}{\sin C} = 8 \]
\[ \Rightarrow \sin C = \frac{1}{2} \Rightarrow \text{m}(\hat C) = 30^\circ \] bulunur.
Örnek:
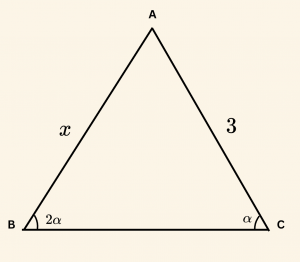Yandaki şekilde verilenlere göre \( \cos \alpha = \frac{3}{4} \) ise \( |AB| = x \) uzunluğunu bulalım.
ABC üçgeninde sinüs teoremi yazılırsa,
\[\begin{aligned} &\frac{x}{\sin \alpha} = \frac{3}{\sin 2\alpha} \\ \\ & \Rightarrow \frac{x}{\sin \alpha} = \frac{3}{2 \sin \alpha \cdot \cos \alpha} \\ \\
&\Rightarrow x = \frac{3}{2 \cos \alpha} = \frac{3}{2 \cdot \frac{3}{4}} = 2 \end{aligned}\]
SORU 43
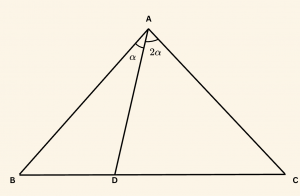
Yandaki ABC üçgeninde
\( \text{m}(\hat {BAD}) = \alpha \)
\( \text{m}(\hat {DAC}) = 2\alpha \)
\( |DC| = 3|BD| \) ise,
\[ \frac{|AB|}{|AC|} \quad \text{oranı nedir?} \]
\[\text{A) } \frac{1}{3} \cos \alpha \quad
\text{B) } \frac{1}{2} \cos \alpha \quad
\text{C) } \frac{2}{3} \cos \alpha \quad
\text{D) } \cos \alpha \quad
\text{E) } 2\cos \alpha
\]
Çözüm:
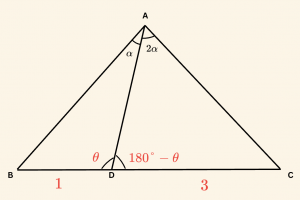
\( |BD| = 1 \) birim seçilirse,
\( |DC| = 3 \) birim olur.
\( \text{m}(\hat {BDA}) = \theta \) ise,
\( \text{m}(\hat {ADC}) = 180^\circ – \theta \) dır.
Sırasıyla ABD ve ADC üçgeninde sinüs teoremini yazarak elde edilen eşitlikleri taraf tarafa bölelim.
\[
\frac{|AB|}{\sin \theta} = \frac{1}{\sin \alpha}
\]
\[
\frac{|AC|}{\sin (180^\circ – \theta)} = \frac{3}{\sin 2\alpha}
\]
\[
\frac{|AB|}{|AC|} = \frac{\sin 2\alpha}{3 \sin \alpha} = \frac{2 \sin \alpha \cdot \cos \alpha}{3 \sin \alpha} = \frac{2}{3} \cos \alpha \text{ dır.}
\]
\(\textbf{Cevab: C} \)
SORU 44
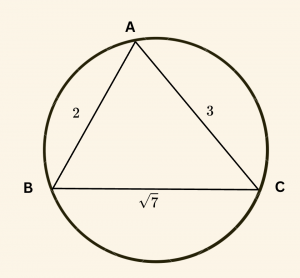
Yandaki şekilde
\( |AB| = 2 \, \text{cm}, \)
\( |AC| = 3 \, \text{cm}, \)
\( |BC| = \sqrt{7} \, \text{cm} \) ise,
ABC üçgeninin çevrel çemberinin yarıçapı kaç cm’dir?
\[
\text{A)} \frac{\sqrt{21}}{2} \quad
\text{B)} \frac{\sqrt{21}}{3} \quad
\text{C)} \frac{\sqrt{10}}{2} \quad
\text{D)} \frac{\sqrt{10}}{3} \quad
\text{E)} 1
\]
Çözüm:
ABC üçgeninde kosinüs teoremi yazılırsa,
\[ (\sqrt{7})^2 = 2^2 + 3^2 \;- \; 2 \cdot 2 \cdot 3 \cdot \cos A \Rightarrow \cos A = \frac{1}{2} \]
\[ \Rightarrow A = 60^\circ \text{ olur.} \]
Şimdi de ABC üçgeninde sinüs teoremini yazalım.
ABC üçgeninin çevrel çemberinin yarıçapının uzunluğu R ise,
\[
\frac{\sqrt{7}}{\sin A} = 2R \Rightarrow \frac{\sqrt{7}}{\sin 60^\circ} = 2R
\]
\[
\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}} = 2R \Rightarrow R = \frac{\sqrt{21}}{3} \text{ cm’dir.}
\]
\(\textbf{Cevab: B} \)
SORU 45
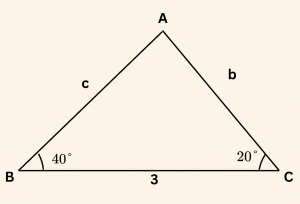
Yandaki şekilde
\( \text{m}(\hat B) = 40^\circ, \quad \text{m}(\hat C) = 20^\circ \) ve \[|AB| = c, \quad |AC| = b, \quad |BC| = 3 \text{ birim} \text{ ise,} \]
\(b + c \) aşağıdakilerden hangisine eşittir?
\[
\text{A) } 2\sqrt{3} (\sin 40^\circ + \sin 20^\circ) \quad
\text{B) } 4 \sin 10^\circ \quad
\text{C) } 5 \cos 10^\circ \quad
\text{D) } 6 \cos 10^\circ \quad
\text{E) } 6 \sin 10^\circ
\]
Çözüm:
Verilenlere göre \( m(\hat A) = 120^\circ \text{ dır.} \)
ABC üçgeninde sinüs teoremi yazılırsa,
\[
\frac{3}{\sin 120^\circ} = \frac{b}{\sin 40^\circ} = \frac{c}{\sin 20^\circ}
\]
Orantının özelliğinden,
\[\begin{aligned}\Rightarrow \frac{3}{\frac{\sqrt{3}}{2}} = \frac{b + c}{\sin 40^\circ + \sin 20^\circ} \\ \\
\Rightarrow b + c = 2\sqrt{3} (\sin 40^\circ + \sin 20^\circ) \end{aligned}\]
\(\textbf{Cevab: A} \)