İrrasyonel (Rasyonel Olmayan) Sayılar
Sayı ekseni üzerinde görüntüsü olan, ancak rasyonel olmayan sayılar irrasyonel sayılar olarak adlandırılır. Bu sayılar, rasyonel bir sayı olarak yazılamaz, yani kesir şeklinde ifade edilemez. İşte bazı önemli irrasyonel sayılar:
- √2(karekök 2): Yaklaşık olarak 1.414, iki tam sayının oranı olarak ifade edilemez ve irrasyoneldir.
- π (pi): Çemberin çevresinin çapına oranı olan bu sayı yaklaşık 3.14159… olarak bilinir ve irrasyoneldir.
- e (Euler sayısı): Doğal logaritmaların tabanı olan e sayısı yaklaşık 2.718’dir ve irrasyoneldir.
- √3 (karekök 3): Yaklaşık 1.732, yine irrasyonel bir sayıdır.
Bu sayılar, sayı doğrusunda belirli bir noktada yer alırlar, ancak kesirli bir şekilde ifade edilemezler. Dolayısıyla, rasyonel olmayan ve irrasyonel olarak adlandırılırlar.
İrrasyonel sayılar, rasyonel olmayan sayılardır. İrrasyonel sayıların kümesi Q’ ile gösterilir. İrrasyonel sayılar ile rasyonel sayıların birleşimi reel sayılar (gerçel sayılar) kümesini oluşturur. Reel sayılar kümesi ise R ile ifade edilir. Buna göre:
\[R= Q\quad\cup\quad Q’\]
Reel sayılar, sayı doğrusunu tamamen doldurur ve sayı doğrusunda her noktaya bir reel sayı karşılık gelir. Bu nedenle sayı doğrusu ile reel sayılar kümesi bire bir eşlenebilir.
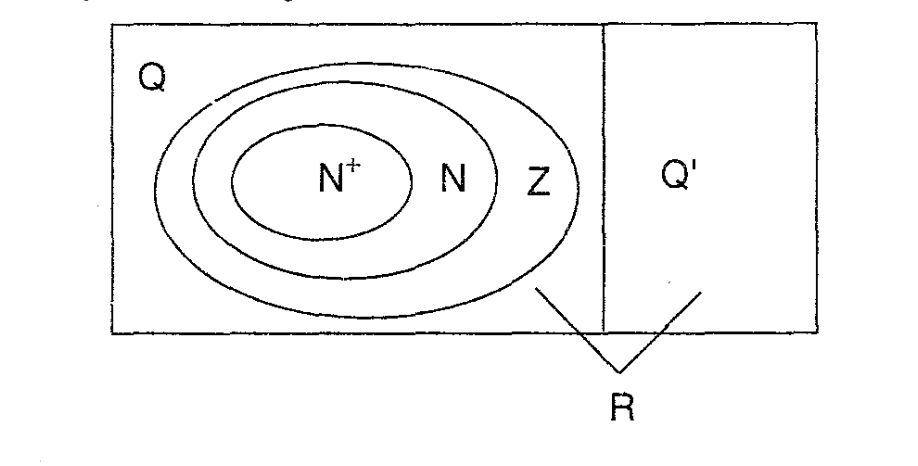
Sayılar, kümeler halinde birbirleriyle ilişkilendirilerek Venn şeması ile gösterilebilir. Bu şema, reel sayılar kümesi (R), rasyonel sayılar kümesi (Q), tam sayılar kümesi (Z) ve doğal sayılar kümesi (N) arasındaki ilişkileri görselleştirir.
$$Z^+ = N^+\subset N \subset Z \subset Q \subset R \quad ve \quad Q’ \subset R $$
Venn Şeması Görünümü
Reel sayılar kümesi (R), hem rasyonel sayıları (Q) hem de irrasyonel sayıları (Q’) kapsar. Aşağıdaki Venn şeması, sayılar arasındaki bu ilişkileri daha iyi anlamamıza yardımcı olur: