Bağıntının Gösterilişi
1) Ortak Özellik Yöntemi:
Bağıntıya ait ikililerin bileşenlerinin ortak özelliği belirtilerek bağıntı gösterilir.
Örnek:
\( A= \{1,2,3 \}\) kümesinde tanımlı, \( R = \{(x, y ) \;|\; x ≤ y \} \) bağıntısında ikililerin birinci bilişeni ikinci bileşenden küçük veya eşittir.
2) Liste Yöntemi:
Örnek:
\( A= \{1,2,3 \}\) kümesinde tanımlı, \( R = \{(x, y ) \;|\; x ≤ y \} \) liste yöntemi ile gösterelim.
\[ R= \{ (1,1 ), (1, 2 ), (1,3), (2,1 ), (2,2 ), (3,3) \} \]
3) Koordinat Diyagramı Yöntemi:
\( R= \{ (1,1 ), (1, 2 ), (1,3), (2,2), (2,3 ), (3,3) \} \) bağıntısını koordinat diyagramı yöntemi ile gösterelim.
Adım 1: Eksenleri Oluşturma
- -ekseni: Bağıntıdaki ilk elemanları (örneğin 1, 2, 3) temsil eder.
- -ekseni: Bağıntıdaki ikinci elemanları (örneğin 1, 2, 3) temsil eder.
Adım 2: Noktaların Yerleştirilmesi
Bağıntı \( R= \{(1,1),(1,2),(1,3),(2,2),(2,3), (3,3) \} \) içerisindeki her bir \( (x,y) \) çifti için, x-ekseni üzerinde x değerini, y ekseni üzerinde y değerini bulup o noktaya bir işaret koyarız:
\[
\begin{aligned}
\bullet \quad (1, 1) : x= 1 , y = 1 \\
\bullet \quad (1, 2) : x= 1 , y = 2 \\
\bullet \quad (1, 3) : x= 1 , y = 3 \\
\bullet \quad (2, 2) : x= 2 , y = 1 \\
\bullet \quad (2, 3) : x= 2 , y = 2 \\
\bullet \quad (3, 3) : x= 3 , y = 3 \\\end{aligned}
\]
Adım 3: Koordinat Diyagramının Çizimi
Aşağıda, eksenler üzerinde işaretlenmiş noktalarla basitleştirilmiş bir koordinat diyagramı örneği bulunmaktadır:
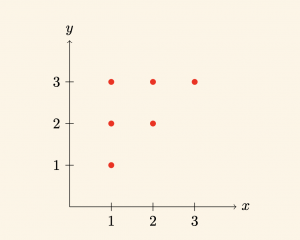
4) Ok Diyagramı Yöntemi:
\( R= \{ (1,1 ), (1, 2 ), (1,3), (2,2), (2,3 ), (3,3) \} \) bağıntısını ok diyagramı yöntemi ile gösterelim.
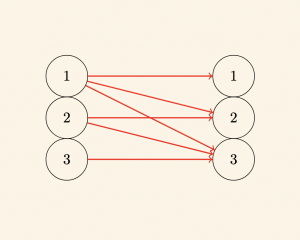
4) Venn Şeması Yöntemi:
\( R= \{ (1,1 ), (1, 2 ), (1,3), (2,2), (2,3 ), (3,3) \} \) bağıntısını Venn Şeması yöntemi ile gösterelim.
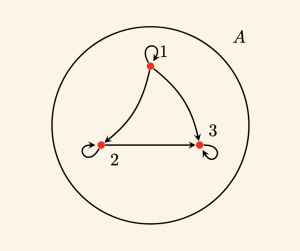
Bağıntı Sayısı:
\(s(A) = n, \;\; s(B)= m \) olsun. A dan B ye tanımlanabilecek bağıntı sayısı, \(A \times B \) nin alt küme sayısı kadardır. O halde A dan B ye bağıntı sayısı
\[ \Large 2^{n \cdot m }\] olur.
Soru 5
\[A = \{x | \; x^2 -x = 0, \; x \in R \} \]
ve
\[B = \{x | \; -2 < x < 7, \; x \in Z^+ \} \]
olduğuna göre, A dan B ye kaç tane bağıntı tanımlanabilir?
\[
\text{A)} 2^{10} \quad
\text{B) } 2^{12} \quad
\text{C) } 2^{14} \quad
\text{D) } 2^{16} \quad
\text{E) } 2^{18}
\]
Çözüm:
\(x^2-x = 0 \Rightarrow x (x-1) =0 \Rightarrow x_1=0 \) veya \( x_2=1 \) bulunur. Buradan \( A = \{0,1 \} \) ve \( s(A) = 2 \) olur.
\( -2 < x < 7 \) ve \( x \in Z^+ \) buradan.
\( B = \{1, 2, 3, 4, 5, 6 \} \) ve \(s(B) = 6 \) olduğundan. A dan B ye bağıntı sayısı \(2^{2 \cdot 6 } = 2^{12} \) dir.
\(\textbf{Cevab: B} \)
Soru 6
\[A = \{x | \frac{12}{x} =k, \;\; \text{ x asal sayı}, k \in Z \]
olduğuna göre, A dan A ye kaç tane bağıntı tanımlanabilir?
\[
\text{A)} 16 \quad
\text{B) } 64 \quad
\text{C) } 128 \quad
\text{D) } 256 \quad
\text{E) } 512
\]
Çözüm:
\[A = \{x | \;\text{x, 12 yi tam bölen asal sayılar } \} \] o halde \( A= \{2,3\} \) olduğundan A dan A ya bağıntı sayısı \( 2^{2 \cdot 2} = 16 \) dır.
Ters Bağıntı:
\(A \) dan \(B \) ye bir \(R = \{ (x,y)\; |\; x \in A \quad \text{ve } y\in B \} \) bağıntısı verilsin.
\(B \) den \(A \) ya \(R^{-1} = \{ (y,x)\; |\; (x,y) \in R \} \) bağıntısına \( R\) nin ters bağıntısı denir.
\[R \subset A \times B \;\; \text{ise } R^{-1} \subset B \times A \;\; \text{ve } (R^{-1})^{-1}= R \; \text{dir.} \]
Uyarı: Bir bağıntıya ait ikililerin bileşenlerinin yerleri değiştirilerek ters bağıntı elde edilir.
Örnek:
\(A = \{1, 2 \}, \; B= \{a, b, c\} \) kümeleri verilsin.
\[ R \subset A \times B \quad \text{ve } \quad R= \{(1, a) , (1,b), (2,c) \}\] ise,
\[ R^{-1} \subset B \times A \quad \text{ve } \quad R^{-1}= \{( a,1 ) , (b,1 ), (c,2 ) \}\] dir.
Örnek:
\( A= \{0,1,2,4,6 \} \) kümesinde tanımlı, \( R = \{ (x,y )| y=x^2 \} \) bağıntısı veriliyor. \(R^{-1} \) bağıntısını liste yöntemi ile yazalım.
\[ x \in A, \;\; y \in A \;\; \text{ve } y= x^2 \;\; \text{olduğuna göre } \]
\[x= 0 \;\; \text{için } y=0 \in A , \;\; x= 4 \;\; \text{için} \;\; y= 16 \not \in A \]
\[x= 1 \;\; \text{için } y=1 \in A , \;\; x= 6 \;\; \text{için} \;\; y= 36 \not \in A \]
\[x= 2 \;\; \text{için } y=4 \in A \] O halde
\[R= \{ (0,0 ), (1,1 ), (2,4) \] ise, \[R^{-1}= \{ (0,0 ), (1,1 ), (4,2) \} \;\;\text{dir} \]
Örnek:
A kümesi: \( A = \{x | -10 ≤x ≤ 10, \, x \in \mathbb{Z} \} \)
Bağıntı: \(
R= \{\, (x,y)|\; y^3= x, (x,y) \in A \times A \}.
\)
olduğuna göre \( R^{-1}\) bağıntısını bulalım.
\[ A= \{ -10, -9.-8 \cdots, 9,10 \} \;\; \text{olduğundan } \]
\[ R = \{(-8,-2), (-1,-1 ), (0,0 ), (1,1 ), (8,2 ) \} \;\; \text{ise } \]
\[ R^{-1} = \{(-2,-8), (-1,-1 ), (0,0 ), (1,1 ), (2,8 ) \} \;\; \text{dir. } \]
Soru 7
\[ R_1 = \{ (x,y) |\; y= x^2, \;\; (x,y) \in Z \times Z\} \]
\[ R_2 = \{ (x,y) |\; x+4y=12, \;\; (x,y) \in Z \times Z\} \]
bağıntıları veriliyor. \(R_1 \cap R_2^{-1} \) aşağıdakilerden hangisidir.
\[
\text{A)} \{(-2, 4 ) \} \quad
\text{B) } \{ (-1, 1) \} \quad
\text{C) } \{ (2, 4), (-6, 36) \} \quad
\text{D) } \{ (-1, 1), (3, 9) \} \quad
\text{E) } \{ (Ø ) \}
\]
Çözüm:
\[R_{2}^{-1}= \{ (x,y) \mid y + 4x = 12,\,(x,y)\in \mathbb{Z}\times \mathbb{Z} \} \]
\[y = x^2\quad \text{ile} \quad y + 4x = 12 \quad \text{ortak çözülürse,} \]
\[ x^2 + 4x – 12 = 0 \quad \Rightarrow \quad (x – 2)(x + 6) = 0 \]
\[\Rightarrow \quad x_1 = 2 \quad \text{veya} \quad x_2 = -6 \]
değerlerini bağıntıların birinde yerine yazalım.
\[y = x^2 \quad \Rightarrow \quad y_1 = 2^2 = 4 \quad \text{ve} \quad y_2 = (-6)^2 = 36 \]
\[ \text{Buradan } R_{1} \cap R_{2}^{-1} = \{ (2,4),\,(-6,36) \} \quad \text{dır.} \]
\(\textbf{Cevab: C} \)
← Önceki Sayfa | Sonraki Sayfa →