Mutlak Değerli Denklemler
\(1. \) \( A ≥0 \) olmak üzere \( \left | f(x) \right | = A \) ise \( f(x) = A \) veya \( f(x) = -A \) dır.
Örnek:
\( \bullet \quad \) \( \left | x \right | = 2 \Rightarrow x = 2 \;\; \) veya \( x = -2 \;\; \) olur, çözüm kümesi ise \(Ç = \{2, -2 \} \)
\( \bullet \quad \) \( \left | x \right | = -2 \Rightarrow Ç = \{ Ø \} \)
\( \bullet \quad \) \( \left | x \right | = 0 \Rightarrow Ç = \{ 2\} \) dır.
Örnek:
\[ \sqrt{\left | 4x^2+1 \right| -4x } + \left| 1 -2x \right | = 6 \] denkleminin çözüm kümesini bulalım.
\( \Rightarrow \left | 4x^2+1 \right| > 0 \) olduğundan \( \left | 4x^2+1 \right| = 4x^2+1 \) olarak mutlak değerin dışına çıkar.
\[ \sqrt{\left | 4x^2+1 \right| -4x } + \left| 1 -2x \right | = 6 \]
\[ \Rightarrow \sqrt{4x^2+1 -4x } + \left| 1 -2x \right | = 6\]
\(2. \) \( \left | f(x) \right| = \left | g(x) \right| \) ise \( f(x) = g(x) \) veya \( f(x) = – \; g(x) \)
Örnek:
\[ \left | 2x-5 \right| = |1-x |\] denkleminin çözüm kümesini bulalım.
\[\begin{aligned}
2x \;- \;5 =& 1 -x \quad &\text{veya } \quad 2x \;- 5 =& \;- \;(1\; -\; x )\\
2x-5 =&1 -x \quad &\text{veya } \quad 2x \;-5 = &\;-1+ x\\
\Rightarrow x = &2 \quad &\text{veya } \quad \Rightarrow x =&4\\
\end{aligned}\]
\(3. \) \( \left | f(x) \right| = g(x) \) ise \( f(x) = g(x) \) veya \( f(x) = – \; g(x) \) tir.
Uyarı:
\( | f(x) | = g(x) \) şeklindeki denklemlerin çözümünde, bulunan \(x \) değerleri verilen denklemde yerine yazılarak, eşitliği sağlayıp sağlamadığı kontrol edilmelidir.
Örnek:
\[ \left| \frac{2x-1}{3} \right| = x-2 \] denkleminin çözüm kümesini bulalım.
\[ \frac{2x-1}{3} = x -2 \Rightarrow x= 5 \] veya \[ \frac{2x-1}{3} = -(x-2) \Rightarrow x = \frac{7}{5} \]
Burada \( x = \frac{7}{5} \) değeri verilen denklemde yerine yazıldığında, \[ \left| \frac{2 \cdot \frac{7}{5} -1}{3} \right| \neq \frac{7}{5} -2 \] bu denklemi sağlamadığı görülür. O halde, \[ Ç = \{5\} \] olarak bulunur.
\(4. \) \( \left | f(x) \right| + \left | g(x) \right| = A \) ise ve \( f(x) \) ile \( g(x) \) in kökleri bulunur. Bulunan bütün kökler sayı doğrusu üzerinde işaretlenir. Elde edilen her bir aralık için denklem ayrı ayrı çözülür. Bulunan çözüm kümelerinin birleşimi alınarak verilen denklemin çözüm kümesi bulunmuş olur.
Örnek:
\[ \left| x\;+ \; 2 \right| \;+ \; \left| x\;-\; 1 \right| \] denklemini sağlayan x tamsayı değerlerini bulalım.
\[\begin{aligned}x+2= 0 \Rightarrow \quad &x = -2 \\ x-1 =0 \Rightarrow \quad &x = 1 \end{aligned}\]
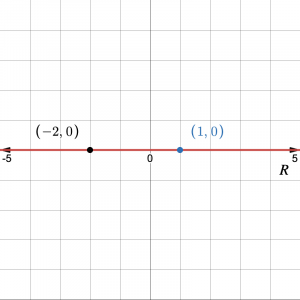
Burada elde edilen üç aralık için çözüm yapılırsa,
\( x ≤ -2 \) için,
\[ – (x + 2 ) + (- (x-1)) = 3 \Rightarrow -2x-1 = 3 \Rightarrow x = -2 \]
\[ -2 ≤ -2\] olduğundan \( Ç_1= \{ -2 \} \)
\(-2 ≤ x ≤ 1 \) için,
\[ (x + 2 ) + (- (x-1)) = 3 \Rightarrow 3= 3 \] olduğundan bu aralıkta her tam sayı değeri eşitliği sağlar. Dolayısıyla, \( Ç_2= \{ -2, -1 , 0 , 1 \} \)
\( x ≥ 1 \) için,
\[ x+ 2 + x – 1 = 3 \Rightarrow 2x+1 = 3 \Rightarrow x = 1 \]
\[ 1 ≤ 1\] olduğundan \( Ç_3= \{ 1 \} \)
Buna göre \( Ç= Ç_1 \cup Ç_2 \cup Ç_3 = \{ -2, -1, 0, 1 \} \) dir.
Soru 32
\[ \left | \frac{2x-1}{5 } \right | = 3 \]
denklemini sağlayan x değerlerinin toplamı kaçtır?
\[
\text{A)} 1\quad
\text{B) } 2 \quad
\text{C)} 3\quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[ \left | \frac{2x-1}{5 } \right | = 3 \Rightarrow \frac{2x-1}{5} = 3 \]
\[ x_1= 8\]
\[ \left | \frac{2x-1}{5 } \right | = 3 \Rightarrow – \left( \frac{2x-1}{5} \right) = 3 \]
\[ x_2= -7 \]
\[ x_1 + x_2 = 8-7 = 1 \]
\(\textbf{Cevab: A} \)
Soru 33
\[ \left | |2x-1| -1 \right | = 3 \]
denklemini sağlayan x değerlerinin çarpımı kaçtır?
\[
\text{A)} 1\quad
\text{B) } -\frac{15}{4} \quad
\text{C)} \frac{15}{4}\quad
\text{D) }- \frac{5}{2} \quad
\text{E) } \frac{5}{2}
\]
Çözüm:
\[ \left | |2x-1| -1 \right | = 3 \]
\( \Rightarrow |2x-1| -1 = 3 \) veya \( |2x-1| -1= -3 \)
\(\Rightarrow |2x-1| = 4 \) veya \( |2x-1| = -2 \Rightarrow Ç= \{ Ø \} \)
\[ |2x-1| = 4 \Rightarrow x_1= \frac{5}{2} \]
veya
\[ |2x-1| = -4 \Rightarrow x_2= -\frac{3}{2} \]
\[x_1 \cdot x_2 = \frac{5}{2} \cdot -(\frac{3}{2} ) = – \frac{15}{4} \]
\(\textbf{Cevab: B} \)
Soru 34
\[ -1 < \left | 2x-5 \right | < 2 \] eşitsizliğini sağlayan kaç tane x tamsayı değeri vardır?
\[
\text{A)} 1\quad
\text{B) } 2 \quad
\text{C)} 3 \quad
\text{D) } 4\quad
\text{E) } 5
\]
Çözüm:
\(x \) tamsayı olduğundan \(2x – 5 \) ifadesi de tamsayı değerler alır. \(-1 \) ile \(2 \) arasındaki tam sayılar \(0 \) ve \( 1 \) dir. Buna göre,
\[ \left | 2x-5 \right | =0 \Rightarrow 2x- 5 =0 \Rightarrow x = \frac{5}{2 } \notin Z \]
\[ \left | 2x-5 \right | =1 \Rightarrow 2x- 5 =1 \Rightarrow x = 3 \] veya
\[ \left | 2x-5 \right | =-1 \Rightarrow 2x- 5 =-1 \Rightarrow x = 2 \]
\(\textbf{Cevab: B} \)
Soru 35
\[ | |x| +1 | + |2x| + | -x | = 9 \] denklemini sağlayan x değerlerinin toplamı kaçtır?
\[
\text{A)} -3\quad
\text{B) } -2 \quad
\text{C)} -1 \quad
\text{D) } 0\quad
\text{E) } 1
\]
Çözüm:
\( |x | ≥ 0 \) dolayısıyla \( |x | +1 ≥ 0 \) olduğundan,
\[ | |x| +1 | = |x| +1 \]
\[ | |x| +1 | + |2x| + |-x | = 9 \]
\[ \Rightarrow |x | + 1 + 2 |x | + |x | =9 \]
\[\Rightarrow 4 |x | = 8 \Rightarrow |x| = 2 \]
\[ x_1= 2 \quad \quad \text{veya } \quad \quad x_2= -2 \]
\[ x_1+ x_2 = 0\]
\(\textbf{Cevab: D} \)
Soru 36
\( a < b < 0 < c\) olmak üzere,
\[ (c+ b- a)^{10} = (a-b- 3 )^{10} \] ise c kaçtır?
\[
\text{A)} 1\quad
\text{B) } 2 \quad
\text{C)} 3 \quad
\text{D) } 4\quad
\text{E) } 5
\]
Çözüm:
\[ (c+ b -a )^{10} = (a-b-3)^{10} \]
\[\Rightarrow |c+ b -a| = |a-b-3| \]
\[\Rightarrow c+b -a = -(a-b-3) \]
\[\Rightarrow c+b -a = -a+b+3 \]
\[\Rightarrow c = 3 \]
\(\textbf{Cevab: C} \)
Soru 37
\( |3x-5| = |2x-1 |\) denklemini sağlayan x tamsayı değeri kaçtır?
\[
\text{A)} 1\quad
\text{B) } 2 \quad
\text{C)} 3 \quad
\text{D) } 4\quad
\text{E) } 5
\]
Çözüm:
\( |3x-5| = |2x-1 |\) ise
\[ 3x-5 = 2x-1 \]
\[ x = 4 \]
veya
\[ 3x-5 = -(2x-1) \]
\[ 3x-5 = -2x+1 \]
\[ x = \frac{6}{5} \neq Z \]
\(\textbf{Cevab: D} \)
Soru 38
\( |x-3| = |3-2x |\) denkleminin çözüm kümesi nedir?
\[
\text{A)} \{-1, 1 \}\quad
\text{B) } \{2 \} \quad
\text{C)} \{0, 2 \} \quad
\text{D) } \{0, 1 \}\quad
\text{E) } \{0\}
\]
Çözüm:
\( |x-3| = |3-2x | \) ise,
\[ x-3 = 3-2x \]
\[ x = 2 \]
veya
\[|x-3| = -(3-2x ) \]
\[|x-3| = -3+2x \]
\[ x =0 \]
\( x = 2 \) için
\[ |x-3 | = 3- 2x \Rightarrow |2-3 | = 3-2 \cdot 2 \]
olduğundan \( x = 2 \) değerleri için sağlamadığı görülür.
\( x= 0 \) için
\( |0-3 | = 3-2 \cdot 0 \Rightarrow |-3| = 3 \)
olduğundan \( x = 0 \) değeri denklemi sağlar. Buna göre,
\[ Ç = \{0\} \]
\(\textbf{Cevab: E} \)
← Önceki Sayfa | Sonraki Sayfa →