İşçi – Havuz Problemleri
İşçi – havuz problemlerinde birim zamanda yapılan işe göre hesaplama yapılır.
Bir işin tamamını, tek başına:
\( \bullet \quad \) A işçisi a günde yaparsa, 1 günde işin \( \large \frac{1}{a} \) sını
\( \bullet \quad \) B işçisi b günde yaparsa, 1 günde işin \( \large \frac{1}{b} \) sini
\( \bullet \quad \) C işçisi c günde yaparsa, 1 günde işin \( \large \frac{1}{c} \) sini ve
A, B ve C işçileri birlikte çalıştıklarında, 1 günde işin \( \large \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \) kadarını tamamlarlar. Bu üç işçi, aynı işi birlikte t günde bitiriyorlarsa, 1 günde işin \( \large \frac{1}{t} \) kısmını yaparlar.
Buna göre \[ \frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{t} \] dir.
Örnek:
Bir işi Uğur tek başına 8 günde, Sinan ise 24 günde tamamlayabilmektedir. İkisinin birlikte, aynı işi kaç günde bitirebileceğini bulalım.
\( \bullet \quad \) Uğur’un bir günde yaptığı iş \( \large \frac{1}{8} \)
\( \bullet \quad \) Sinan’ın bir günde yaptığı iş \( \large \frac{1}{24} \)
İkisi birlikte çalıştığında, bir günde yapacakları iş miktarı:
\[ \frac{1}{8} + \frac{1}{24} = \frac{1}{x} \Rightarrow x=6 \quad \text{gün bulunur. } \]
Örnek:
Üç isçi bir işin tamamını, birlikte 4 günde bitirebilmektedir. Aynı işi, tek başına birinci isçi 9, ikinci isçi 12 günde bitirebildiğine göre, üçüncü isçinin tek başına bu işi kaç günde bitirebileceğini bulalım.
Üçüncü isçi, işin tamamını tek başına x günde yapsın.
\[ \frac{1}{9} + \frac{1}{12} + \frac{1}{x} = \frac{1}{4} \Rightarrow x = 18 \]
Uyarı:
Bir işi, \(A, B \) ve \( C \) isçileri, tek başlarına, sırasıyla \( a, b \) ve \( c \) günde bitiriyor olsun. \(A, B \) ve \(C \) işçileri, bu işin \( m \) kadarını \( t \) günde bitirirlerse,
\[
\begin{aligned}
1 \quad günde \quad \quad \quad \quad \quad &\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \\
\\
t \quad günde \quad \quad \quad \quad \quad &m \quad \text{kadarını bitirebilirler.} \\
\hline
\\
\quad \quad \quad \quad \quad \quad \quad \quad \quad \text{Doğru Orantı}
\end{aligned}
\]
şeklinde orantı kurulur. Buradan
\[ ( \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \cdot t ) = m \] eşitliği elde edilir.
Örnek:
Bir işin tamamını, tek başlarına, Murat 4 günde, Yunus 8 günde bitirebiliyor. İkisinin, birlikte, bu işin \( \Large \frac{3}{8} \) ini kaç günde günde bitirebileceğini bulalım.
Problemde verilenler \[ \frac{1}{a} + \frac{1}{b} = \frac{1}{t} \cdot m \] eşitliğinde yerine yazılırsa \[ \frac{1}{4} + \frac{1}{8} = \frac{1}{t} \cdot \frac{3}{8} \Rightarrow t = 1 \] gün bulunur.
Örnek:
Yavuz bir işi \( \large \frac{2}{3} \) günde, Selim ise aynı işi \( \large \frac{x}{2} \) günde bitirebiliyor. İkisi birlikte bu işin yarısını 6 günde bitirebildiğine göre, Yavuz’un bu işi tek başına kaç günde bitirebileceğini bulalım.
Problemde verilenlere ait denklem
\[\frac{1}{\frac{2x}{3} } + \frac{1}{\frac{x}{2} } = \frac{1}{6} \cdot \frac{1}{2} \]
şeklinde yazılırsa \( x = 42 \) olur. O halde Yavuz bu işi tek başına
\[\frac{2x}{3} = \frac{2 \cdot 42}{3} = 28 \quad \text{günde bitirir. } \]
Örnek:
Üç işçi beraber bir işin \(\large \frac{3}{4} \) 6 günde bitirebiliyor. Aynı işi, tek başlarına birinci işçi 48, ikinci işçi 16 günde bitirebildiğine göre, üçüncü işçinin bu işi tek başına kaç günde bitirebileceğini bulalım.
Üçüncü işçi, bu işin tamamını, tek başına \(x \) günde bitiriyor olsun. Buna göre verilen probleme ait denklem:
\[ \frac{1}{48} + \frac{1}{16} + \frac{1}{x} = \frac{1}{6} \cdot \frac{3}{4} \Rightarrow x= 24 \] bulunur.
Uyarı:
Bir havuzun tamamını, tek başına; A musluğu a saatte, B musluğu b saatte dolduruyor, bir C musluğu ise aynı havuzun tamamını, tek başına c saatte boşaltıyor olsun. Muslukların üçü birlikte t saat açık bırakıldıkları zaman havuzun m kadarını doldururlarsa
\[ (\frac{1}{a} + \frac{1}{b} – \frac{1}{t}) \cdot t= m \] eşitliği yazılabilir.
Örnek:
Bir havuzun tamamını bir A musluğu tek başına a saatte doldurabilmekte, bir B musluğu ise aynı havuzu, havuz dolu iken tek başına b saatte boşaltabilmektedir.
Havuz boşken, iki musluk c saat açık tutulduğu zaman havuz taştığına göre, a, b ve c arasındaki bağlantıyı bulalım.
İki musluk birlikte açıldığı zaman havuz t saatte dolarsa,
\[ \frac{1}{a} – \frac{1}{b} \cdot t = 1 \]
eşitliği yazılır. Musluklar c saat açık tutulduğunda havuz taştığına göre,
\[ \frac{1}{a} – \frac{1}{b} \cdot c > 1 \]
olur. Buna göre, bu eşitsizlik düzenlenirse,
\[ (b-a ) c > ab\] bağıntısı bulunur.
Örnek:
Boş bir havuzun tamamını, tek başlarına A ve B muslukları sırasıyla 16 ve 24 saatte doldurabilmektedir. Havuzun dibinde ise havuzu boşaltan bir C musluğu vardır. Üç musluk aynı anda açıldığı zaman, havuzun yarısı 24 saatte dolduğuna göre, havuz doluyken C musluğunun, havuzu kaç saatte boşaltabileceğini bulalım.
Havuzun dibindeki C musluğu, dolu havuzun tamamını x saatte boşaltıyor olsun. Buna göre, verilen probleme ait denklem
\[ ( \frac{1}{16} + \frac{1}{24} – \frac{1}{x} ) \cdot 24 = \frac{1}{2} \] şeklinde yazılırsa \[ x = 12 \] bulunur.
Soru 10
Üç işçi bir işi birlikte x günde bitirebilmektedir. Tek başlarına işin tamamını, birinci işçi 2x, ikinci işçi ise x+6 günde bitirebilmektedir. Tek başlarına birinci işçi 1 gün, ikinci işçi 2 gün çalıştığı zaman işin yarısı bittiğine göre, üçüncü işçi bu işi tek başına kaç günde bitirebilir?
\[
\text{A)} 2 \quad
\text{B) } 4 \quad
\text{C) } 6 \quad
\text{D) } 8 \quad
\text{E) } 10
\]
Çözüm:
Birinci işçi 1 günde işin \(\large \frac{1}{2x} \) ’ini, ikinci işçi 2 günde \(\large \frac{2}{x+6} \) sını bitirir. Buna göre,
\[ \frac{1}{2x} + \frac{2}{x+6} = \frac{1}{2} \] şeklinde eşitlik yazılırsa,
\[\begin{aligned} \frac{2}{x+6} = \frac{1}{2} \cdot \frac{x}{x} \; – \; \frac{1}{2x} \Rightarrow \frac{2}{x+6} = \frac{x-1}{2x} \\ \\ \Rightarrow 2 \cdot 2x = (x-1) \cdot (x+ 6 ) \\ \\ \Rightarrow x^2+x -6= 0 \Rightarrow (x+3) \cdot (x-2) = 0 \end{aligned}\]
\[ x_1 = -3 \quad \text{veya } \quad x_2 = 2 \] elde edilir. Çalışma süresi negatif olamayacağından \( x = 2 \) dir.
Üçüncü isçi tek başına işin tamamını y günde bitiriyor olsun. Üç isçi birlikte işin tamamını x günde bitirebildiğine göre,
\[ \frac{1}{2x} + \frac{1}{x+6} + \frac{1}{y} = \frac{1}{x} \Rightarrow \frac{1}{4} + \frac{1}{8} + \frac{1}{y} = \frac{1}{2} \]
\[y =8 \] bulunur
\(\textbf{Cevab: D} \)
Soru 11
İki musluk bir havuzun tamamını 12 saatte doldurabilmektedir. İki musluk birlikte 8 saat su akıttıktan sonra üçüncü bir musluk daha açılıyor. Havuzun geriye kalan boş kısmını, üç musluk 2 saatte doldurabildiğine göre, üçüncü musluk, havuzun tamamını, tek başına kaç saatte doldurabilir?
\[
\text{A)} 9 \quad
\text{B) } 10 \quad
\text{C) } 12 \quad
\text{D) } 15 \quad
\text{E) } 16
\]
Çözüm:
İki musluk birlikte havuzun tamamını 12 saatte doldurabildiğine göre, 8 saatte havuzun \(\Large \frac{8}{12} \) si dolar. Geriye, havuzun \(\Large \frac{4}{12} = \frac{1}{3} \) ü boş kalır.
Üçüncü musluk, havuzun tamamını tek başına x saatte dolduruyor olsun. Birinci ve ikinci musluk birlikte 1 saatte havuzun \(\Large \frac{1}{12} \) sini, üçüncü musluk ise \(\Large \frac{1}{x} \) ini doldurur. Böylece, üç musluk birlikte 1 saatte havuzun
\[ \frac{1}{12} + \frac{1}{x} \]
kısmını doldurmuş olur.
Üç musluk, havuzun boş kalan \( \Large \frac{1}{3} \) lük kısmını 2 saatte doldurabildiğine göre,
\[ \left(\frac{1}{12} + \frac{1}{x} \right)\cdot 2 = \frac{1}{3} \]
denklemini yazarız. Bu eşitliği çözersek:
\[ \frac{1}{12} + \frac{1}{x} = \frac{1}{6} \]
\[ \frac{1}{x} = \frac{1}{6} – \frac{1}{12} = \frac{1}{12} \]
\[ x = 12 \]
Soru 12
İki işçi bir işi birlikte 15 günde bitirebilmektedir. Birinci işçi tek başına 4 gün çalıştıktan sonra, ikinci işçi çalışmaya başlıyor. İşin kalan kısmını, iki işçi birlikte 13 günde tamamlayabildiğine göre, birinci işçi tek başına çalışsaydı işin tamamını kaç günde bitirebilirdi?
\[
\text{A )} 30 \quad
\text{B) } 28 \quad
\text{C) } 27 \quad
\text{D) } 25 \quad
\text{E) } 24
\]
Çözüm:
İki işçi birlikte işin tamamını 15 günde bitirebildiğine göre, bir günde \(\Large \frac{1}{15}\)’ini, 13 günde \(\Large \frac{13}{15}\)’ini bitirebilirler.
O halde birinci isçinin tek başına çalışarak 4 günde bitirdiği kısım, işin \( \Large \frac{2}{15} \) idir. Buna göre, birinci isçi, işin
\[
\begin{aligned}
\quad &\frac{2}{15}\; \text{ini} \quad \quad \quad \quad \quad \quad 4 \quad \text{günde bitirirse} \\
\\
\\
\quad &\frac{15}{15}\; \text{ini} \quad \quad \quad \quad \quad \quad x \quad \text{günde bitirir} \\
\hline \\
\end{aligned}
\]
\[ x \cdot \frac{2}{15} = 1 \cdot 4 \Rightarrow x = 30\]
\(\textbf{Cevab: A} \)
Soru 13
Bir havuzu, tek başlarına A, B ve C muslukları, sırasıyla 12, 36 ve 72 saatte doldurabilmektedir. Üç musluk birlikte açıldıktan sonra, üçer saat arayla, önce C musluğu, daha sonra B musluğu kapatılıyor. Buna göre, B musluğu kapatıldıktan sonra, havuzun geriye kalan boş kısmını A musluğu kaç saatte doldurur?
\[
\text{A )} 1,5 \quad
\text{B) } 2 \quad
\text{C) } 2,5 \quad
\text{D) } 3 \quad
\text{E) } 3,5
\]
Çözüm:
A, B ve C muslukları, tek başlarına havuzun tamamını sırasıyla 12, 36 ve 72 saatte doldurduğuna göre, bir saatte doldurdukları oranlar şu şekilde hesaplanır: \[ A \text{ musluğu } \frac{1}{12}, \quad B \text{ musluğu } \frac{1}{36}, \quad C \text{ musluğu } \frac{1}{72} \] B musluğu kapatılıncaya kadar A ve B musluğundan 6 saat, C musluğundan ise 3 saat su akmıştır. Bu süre boyunca musluklardan toplam akan su miktarı: \[ 6 \times \frac{1}{12} + 6 \times \frac{1}{36} + 3 \times \frac{1}{72} = \frac{6}{12} + \frac{6}{36} + \frac{3}{72} = \frac{17}{24} \] Havuzun dolan kısmı \(\frac{17}{24}\) olduğuna göre, geriye kalan boş kısmı: \[ 1 – \frac{17}{24} = \frac{7}{24} \] Bu kalan kısmı A musluğu tek başına dolduracaktır. A musluğu 1 saatte havuzun \(\frac{1}{12}\)’sini doldurduğuna göre, \(\frac{7}{24}\)’lük kısmı \(x\) saatte doldurur. Doğru orantı kurulursa: \[ \frac{1}{12} \rightarrow 1 \text{ saat} \quad \Rightarrow \quad \frac{7}{24} \rightarrow x \text{ saat} \] Buradan: \[ \frac{1}{12} \cdot x = \frac{7}{24} \quad \Rightarrow \quad x = \frac{7}{24} \cdot 12 = 3,5 \text{ saat} \] Sonuç olarak, B musluğu kapatıldıktan sonra A musluğu, havuzun geriye kalan kısmını 3,5 saatte doldurur.
\(\textbf{Cevab: E} \)
Soru 14
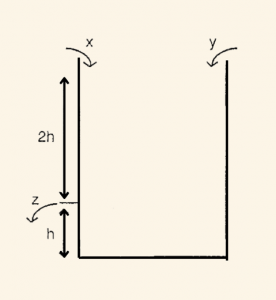
Şekilde verilen x ve y musluğu birlikte, z musluğu kapalıyken, boş havuzu 36 saatte doldurabiliyor. Tabanından itibaren havuzun 1/3 yüksekliğinde bulunan z musluğu ise tek başına havuzun 2/3’ünü 36 saatte boşaltabiliyor.
Havuz boşken muslukların üçü birlikte açılırsa, havuzun tamamı kaç saatte dolar?
\[
\text{A )} 72 \quad
\text{B) } 76 \quad
\text{C) } 80 \quad
\text{D) } 84 \quad
\text{E) } 86
\]
Çözüm:
Tabandan itibaren havuzun \(\Large \frac{1}{3} \) yüksekliğine kadar olan kısmının dolma süresi \( t_1\) , kalan kısmının dolma süresi \( t_2\) olsun. Su seviyesi, z musluğunun olduğu yüksekliği gelinceye kadar, x ve y musluğu havuzu \( t_1\) sürede dolduracaktır. Buradan x ve y musluğu birlikte, havuzun
\[
\begin{aligned}
\\&36 \; \text{saatte} \quad \quad \quad \quad &\frac{3}{3} \; \text{ünü doldurursa }
\\
\\
\\ &t_1 \; \text{saatte} \quad \quad \quad \quad &\frac{1}{3} \; \text{ünü doldurur}
\\
\hline
\\
\text{Doğru orantı}
\end{aligned}
\]
x ve y muslukları havuzun geriye kalan kısmını birlikte \[ 36 \cdot \frac{2}{3} = 24 \] saatte doldurabileceğine göre, 1 saatte 1/24’ünü doldurur. z musluğu ise havuzun bu kısmını 36 saatte boşaltabildiğine göre, 1 saatte 1/36’sını boşaltır.
Buna göre, x, y ve z muslukları birlikte açıldığı zaman, havuzun boş kalan kısmını t₂ sürede doldururlarsa:
\[ \frac{1}{24} – \frac{1}{36} = \frac{1}{t_2} \Rightarrow t_2= 72 \; \text{saat bulunur.} \]
o halde, boş havuzun tamamının dalma süresi,
\[ t_1 + t_2 = 12 + 72 = 84 \; \text{saattir.} \]
\(\textbf{Cevab: D} \)
Soru 15
Emre, Erdem’in iki katı, Metin’in de yarısı hızla çalışmaktadır. Metin ile Erdem birlikte, bir işi 12 günde bitirebilmektedir.
Aynı işi, Emre ile Metin birlikte, kaç günde bitirebilir?
\[
\text{A )} 10 \quad
\text{B) } 12 \quad
\text{C) } 14 \quad
\text{D) } 15 \quad
\text{E) } 16
\]
Çözüm:
Metin işin tamamını x günde bitiriyor olsun.
Buna göre Emre ve Erdem’in tek başlarına, işin tamamını bitirme süreleri sırasıyla 2x ve 4x olur. Metin ile Erdem birlikte, işin tamamını 12 günde bitirebildiklerine göre:
\[ \frac{1}{x} + \frac{1}{4x} = \frac{1}{12} \Rightarrow x= 15 \] bulunur.
Emre ile Metin birlikte, işin tamamını t günde bitiriyor olsunlar. Buradan:
\[\frac{1}{2x} + \frac{1}{x} = \frac{1}{t} \Rightarrow \frac{3}{2x} = \frac{1}{t} \]
\[ \frac{3}{2 \cdot 15} = \frac{1}{t} \Rightarrow t = 10 \] gün olur
\(\textbf{Cevab: A} \)
← Önceki Sayfa | Sonraki Sayfa →