Fonksiyonlar
A ve B boş olmayan iki küme olmak üzere, A’dan B’ye bir \( f\) bağıntısı tanımlansın. Eğer A’nın her elemanı \( f\) bağıntısı ile B’nin sadece bir elemanına eşlenmiş ise \( f\) bağıntısına A’dan B’ye bir fonksiyon denir.
\[ f: A \longrightarrow B \quad \text{veya} \quad A \rightarrow{f} B \]
şeklinde gösterilir.
A’ya fonksiyonun tanım kümesi, B’ye değer kümesi denir. Ayrıca, A kümesinin elemanlarının B kümesinde eşleştiği elemanlardan meydana gelen kümeye A’nın görüntü kümesi denir ve \( f(A) \) ile gösterilir.
Örnek:
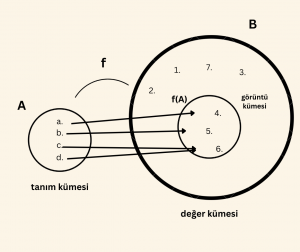
\(A = \{ a, b, c, d \} \) tanım kümesi,
\( B = \{ 1, 2, 3, 4, 5, 6, 7 \} \) değer kümesi
\( f(A) = \{ 4, 5, 6 \} \) görüntü kümesi ve \( f(A) \subseteq B \) dir.
\( f: A \to B \) ve \( (x,y) \in f \) ise,
\( f: x \to y \) veya \( y = f(x) \) şeklinde gösterilir ve \( x \) in \( f \) altındaki görüntüsü \( y \) dir denir.
Örnek:
\( A = \{ -1, 0, 1, 2 \} \) ve \( B = \{ -1, 0, 1, 2, 3, 4 \} \) kümeleri veriliyor. A’dan B’ye \( f \) fonksiyonu,
\[
f = \{ (x, y) \mid y = x^2 \}
\]
şeklinde tanımlansın. Bu durumda \( f \) fonksiyonu,
\[
f(x) = x^2
\]
ve
\[ x = -1 \quad \text{için} \quad f(-1) = (-1)^2 = 1 \]
\[x = 0 \quad \text{için} \quad f(0) = 0^2 = 0 \]
\[x = 1 \quad \text{için} \quad f(1) = 1^2 = 1 \]
\[x = 2 \quad \text{için} \quad f(2) = 2^2 = 4 \]
\( f = \{ (-1, 1), (0, 0), (1, 1), (2, 4) \} \) ve ok diyagramı ile şeklinde gösterilir. Görüntü kümesi ise,
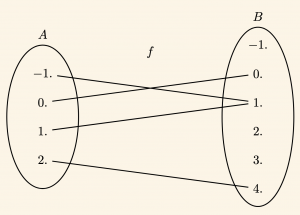
\[ f(A) = \{ 0, 1, 4 \} \]
Uyarı:
A dan B ye tanımlanan \(f \) bağıntısının fonksiyon olması için;
\(1) \) A da görüntüsü olmayan (açıkta) eleman olmamalı, fakat B de boşta eleman kalabilir.
\( 2) \) A daki bir veya daha fazla elemanın B de sadece bir görüntüsü olmalıdır.
Örnekler:
\( A = \{ a, b, c \} \) ve \( B = \{ 1, 2, 3 \} \) kümeleri veriliyor. A dan B ye tanımlanan aşağıdaki bağıntıların fonksiyon olup olmadıklarını inceleyelim.
\[
\bullet \quad f_1 = \{ (a, 1), (b, 3) \} \quad \text{bağıntısını ok diyagramı ile gösterelim.}
\]
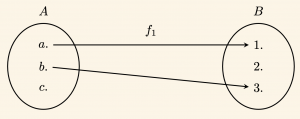
A da açıkta eleman kaldığından \( f_1 \) bağıntısı fonksiyon değildir.
\[
\bullet \quad f_2 = \{ (a, 1), (b,2), (b, 3), (c, 3) \} \quad \text{bağıntısını ok diyagramı ile gösterelim.}
\]
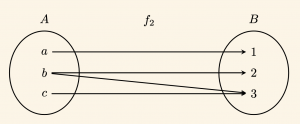
\( A\) daki b elemanının \(B \) de 2 ve 3 gibi farklı iki görüntüsü olduğundan \( f2\) bağıntısı fonksiyon değildir.
\[
\bullet \quad f_3 \quad \text{bağıntısını ok diyagramı ile gösterelim.}
\]
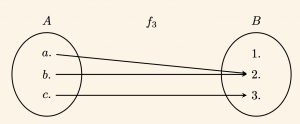
\(f_3 \) bağıntısı fonksiyon olma şartlarını sağladığından fonksiyondur.
\[
\bullet \quad f_4 \quad \text{bağıntısını ok diyagramı ile gösterelim.}
\]
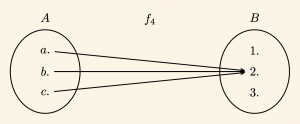
\(f_4 \) bağıntısı fonksiyon olma şartlarını sağladığından fonksiyondur.
Örnek:
\( A = \{ -2, -1, 1, 2 \} \) kümesinde \(f \) bağıntısı aşağıdaki gibi tanımlanmıştır.
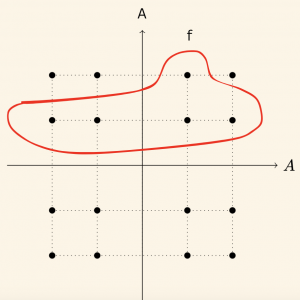
Ok diyagramını çizelim
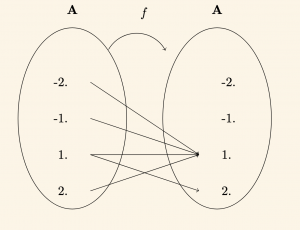
Tanım kümesindeki 1 elemanının değer kümesinde 1 ve 2 gibi farklı iki görüntüsü oldugundan \(f \) bağıntısı fonksiyon degildir.
Örnekler:
Aşağıdaki verilen bağıntılarının fonksiyon olup olmadıklarını inceleyelim.
1) \(\mathbb{R} \) den \(\mathbb{R} \) ye tanımlanan
\[
f_1 = \{(x,y) \mid y = \frac{x}{x^2 – 1} \}
\]
\[ y = \frac{x}{x^2 – 1} \quad \text{bağıntısı} \]
\( x = \pm1 \) için payda sıfır olacağından \(\large \frac{x}{x^2 – 1} \) ifadesi tanımsız olur. O halde tanım kümesinde \( -1 \) ve \( 1 \) elemanları açıkta kaldığından \( f_1 \) bağıntısı fonksiyon değildir.
2) \( \mathbb{R} \) ‘den \( \mathbb{R} \) ‘ye tanımlanan
\[
f_2 = \{(x,y) \mid |y| = x^2 + 1 \}
\]
\[ |y| = x^2 + 1 \quad \text{bağıntısı} \] Tanım kümesindeki her elemanın iki görüntüsü vardır. Örneğin, \( x = 1 \) için \( y = \pm 2 \) gibi…
Bu durumda, \( f_2 \) bağıntısı fonksiyon değildir.
3) \( \mathbb{R} \) ‘den \( \mathbb{R} \) ‘ye tanımlanan
\[
f_3 = \{(x,y) \mid y = \frac{x}{x^2 + 1} \}
\]
\( x \) ‘in her reel sayı değeri, yalnızca bir tek \( y \) reel sayı değeri ile eşleneceğinden \( f_3 \) bağıntısı fonksiyondur.
4) \( \mathbb{Z} \) ‘den \( \mathbb{Z} \) ‘ye tanımlanan
\[
f_4 = \{(x,y) \mid y = \frac{x – 1}{3} \}
\]
bağıntısının tanım kümesinde açıkta eleman kalır. Örneğin \( x= 2 \) için \(y= \frac{1}{3} \) olduğu için 2 elemanı tanım kümesinde açıktadır. O halde \(f_4 \) bağıntısı fonksiyon değildir.
Uyarı:
Grafiği verilen bir bağıntının fonksiyon olup olmadığını anlamak için bağıntının tanım kümesinin her noktasıdan Ox eksenine dikmeler çizilir:
1)Grafiği kesmeyen dikme kalmıyor,
2) Dikmelerin her biri grafiği sadece birer noktada kesiyor ise bu bağıntı, bir fonksiyondur.
Örnek:
\( (x, y) \in f \) olmak üzere, \( \mathbb{R} \) ‘den \( \mathbb{R} \) ‘ye tanımlanan \( f \) bağıntısının grafiği verilmiştir.
Bu bağıntının fonksiyon olup olmadığını inceleyelim.
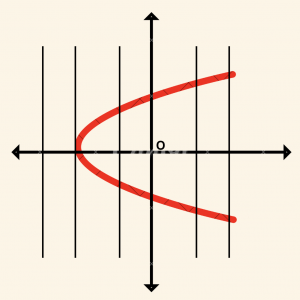
\(f \) bağıntısının tanım kümesi reel sayılar kümesi olduğundan, Ox ekseni üzerindeki her noktadan dikmeler çizilir. Grafiği kesmeyen dikmeler ile grafiği birden fazla (iki) noktada kesen dikmeler var. Bu durumda fonksiyon olma şartlarının ikisi de sağlanmıyor. O halde \( f \) bağıntısı fonksiyon değildir.
Burada, grafiği kesmeyen dikmelerin olması, tanım kümesinde açıkta elemanların bulunması demektir. Grafiği birden fazla noktada kesen dikmelerin olması ise tanım kümesindeki bir elemanın değer kümesinde birden fazla görüntüsünün bulunması anlamına gelir.
Örnekler:
\( (x,y ) \in f \) olmak üzere, verilen bağıntıların fonksiyon olup olmadığını inceleyelim.
1)
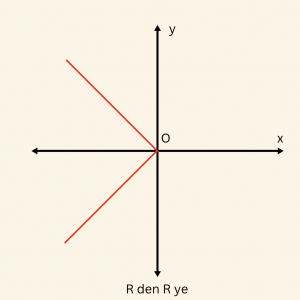
Grafiği kesmeyen dikmeler ve grafiği iki noktada kesen dikmeler var. O halde \( f1\) bağıntısı fonksiyon değildir.
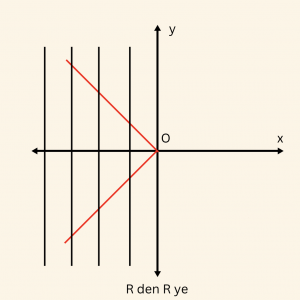
2)
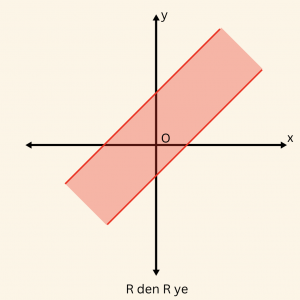\(\Rightarrow \)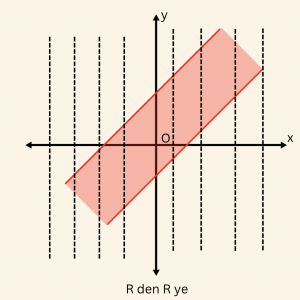 
Grafiği kesmeyen dikme yoktur, fakat bu dikmeler grafiği sonsuz noktada kestiğinden \(f_2\) bağıntısı fonksiyon değildir.
3)
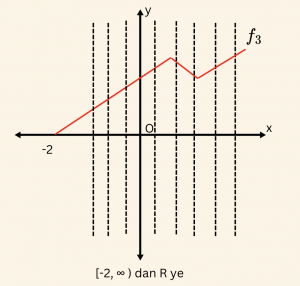
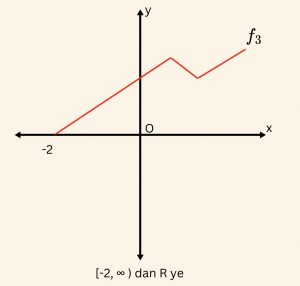\(\Rightarrow \)
Grafiği kesmeyen dikme yoktur ve bu dikmeler grafiği birer noktada kesiyor. O halde \(f_3 \) bağıntısı fonksiyondur.
4)
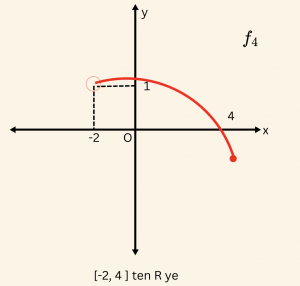\(\Rightarrow \)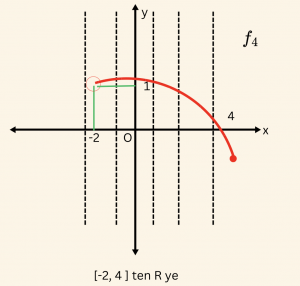 
\( (-2,1 ) \) noktası grafiğe ait olmadığından \(x= -2 \) doğrusu grafiği kesmez. O halde grafiği kesmeyen dikme var ( \(-2 \) tanım kümesinde açıktadır. ) ve \( f_4\) bağıntısı fonksiyon değildir.
5)
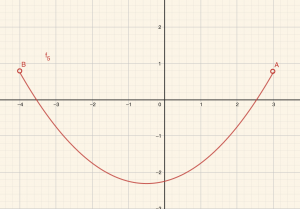
Grafiği kesmeyen dikme yok ve bu dikmeler grafiği birer noktada kesiyor. O halde \( f_5\) bağıntısı fonksiyondur.
Fonksiyon Sayısı:
\( s(A)=m \) ve \( s(B)= n \) ise \(A \) dan \( B \) ye tanımlanabilecek fonksiyonların sayisi
\[ \Large n^m \]
Soru 9
\[ A = \{ 1,2,3 \} \quad \text{ve } \quad B= \{ a, b, c, d \} \] kümeleri veriliyor. A dan B ye, kaç tane fonksiyon olmayan bağıntı tanımlanabilir?
\[
\text{A)} 4026 \quad
\text{B) } 4028 \quad
\text{C) } 4030 \quad
\text{D) } 4032 \quad
\text{E) } 4034
\]
Çözüm:
A dan B ye bağıntı sayısı: \( 2^{3 \cdot 4} = 2^{12} \)
A dan B ye fonksiyon sayısı: \( 4^3 \)
A dan B ye fonksiyon olmayan bağıntı sayısı: \( 2^{12}\;- \; 4^3 = 4032 \) dir.
\(\textbf{Cevab: D} \)