Fonksiyon Çeşitleri
1. İçine Fonksiyon:
2. Örten Fonksiyon:
3. Bire Bir Fonksiyon:
4. Sabit Fonksiyon:
5. Birim Fonksiyon:
6. Bir Fonksiyonun Tersi:
7. Bileşke Fonksiyon:
8. Permütasyon Fonksiyon:
9 Parçalı Fonksiyon:
10. Tek ve Çift Fonksiyonlar:
1. İçine Fonksiyon:
\( f: A \to B \) fonksiyonu verilsin. \( B \) (değer kümesi) de boşta eleman kalıyorsa bu fonksiyona içine fonksiyon denir.
Yani \( f(A) \neq B \) dir.
Örnekler:
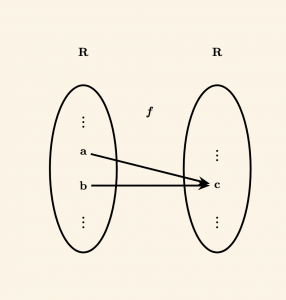
\( \bullet \quad f: A \to B \) fonksiyonu, \( B \) değer kümesinde \( a \) elemanı boşta kaldığından içine fonksiyondur.
\[
A = \{1,2,3\}, \quad B = \{a, b, c\}
\]
Fonksiyon ilişkileri:
\[
f(1) = b, \quad f(2) = b, \quad f(3) = c
\]
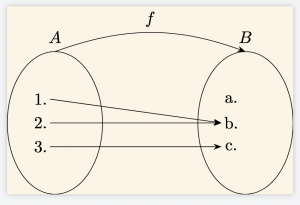
Burada \( a \) elemanı boşta kaldığı için içine fonksiyon olur.
\( \bullet \quad f: \mathbb{Z}^+ \to \mathbb{Z}^+ \),
\[
f(x) = x^2
\]
fonksiyonu, değer kümesinde boşta elemanlar kaldığından içine fonksiyondur.
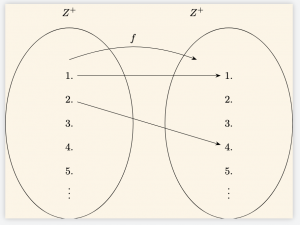
Örneğin,
\[
f(1) = 1, \quad f(2) = 4, \quad f(3) = 9, \quad f(4) = 16, \quad f(5) = 25, \dots
\]
Bu fonksiyonda bazı pozitif tam sayılar (örneğin 2, 3, 5 gibi) hiçbir \( x \) değeri için görüntü olarak alınmadığından içine fonksiyon olur.
2. Örten Fonksiyon:
\( s(A) ≥ s(B)\) olmak üzere,
\(f: A \to B \) fonksiyonu verilsin. B (değer kümesi) de boşta eleman kalmıyorsa bu fonksiyona örten fonksiyon denir. Yani \( f(A) = B \) dir.
Örnekler:
1) \(f: \;A \to B\) fonksiyonu, \(B\) değer kümesinde boşa eleman kalmadığından ötürü örten fonksiyondur.
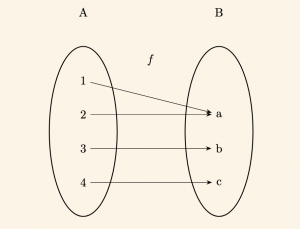
2) \(f: \;N \to N \quad f(x) = 2x+1 \) fonksiyonu, \(N\) değer kümesinde boşta eleman kaldığından ötürü örten değildir. O halde içine fonksiyondur.
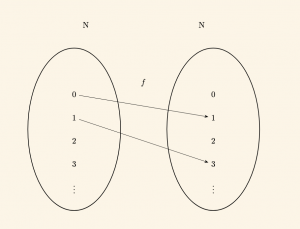
3) \(f: \;Z \to R \quad f(x) = 3x-2 \) fonksiyonu, \(R\) değer kümesinde boşta elemanlar kaldığından \(( f(Z) \neq R )\) ötürü örten fonksiyon değildir. O halde içine fonksiyondur.
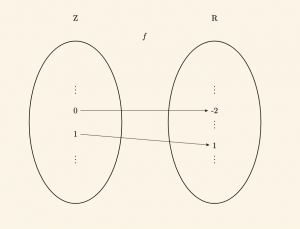
Uyarı:
\(f: A \to B, \;\; y= f(x) \) fonksiyonunun örten olup olmadığını anlamak için \(x,y \) cinsinden bulunur. y yerine yazılacak B nin her elemana karşılık, elde edilen x değeri A nın bir elemanı ise bu fonksiyon örtendir.
Örnek:
\( f: \mathbb{Z} \to \mathbb{Z}, \quad y = f(x) = 2x + 3 \) fonksiyonunun örten olup olmadığını inceleyelim.
\( y = 2x + 3 \Rightarrow x = \frac{y – 3}{2} \) olur. Burada \( y \) nin her tamsayı değeri için \( x \) tamsayı olmayacağından bu fonksiyon örten değildir. O halde içine fonksiyondur.
Örneğin \( y = 4 \) için \( x = \frac{4 – 3}{2} = \frac{1}{2} \notin \mathbb{Z} \) dir.
SORU 19
\[ s(A) = n^2\; -\; 4 \quad \text{ve } \quad s(B) = 3n \] ise \( f: \; A \to B \) fonksiyonunun örten olabilmesi için \( n \) en az kaç olmalıdır?
\[
\text{A) } 1 \quad
\text{B) } 2 \quad
\text{C) } 3\quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\( f: A \to B \) fonksiyonunun örten olabilmesi için \( s(A) \geq s(B) \) olmalıdır. \( s(A) < s(B) \) iken bu fonksiyonun örten olması mümkün değildir.
\[ s(A) \geq s(B) \Rightarrow n^2 – 4 \geq 3n \] \[ \Rightarrow n^2 – 3n – 4 \geq 0 \] \[ \Rightarrow (n – 4)(n + 1) \geq 0 \] olması için, \( n + 1 > 0 \) olduğundan \( n – 4 \geq 0 \) olmalıdır.
O halde \( n \) en az 4 değerini alır.
\(\textbf{Cevab: D} \)
3. Bire Bir Fonksiyon:
\( s(A) \leq s(B) \) olmak üzere,
\( f: A \to B \) fonksiyonu verilsin. A kümesinin her elemanının görüntüsü farklı ise bu fonksiyona bire bir fonksiyon denir.
Yani \( y = f(x) \) için,
\[
x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2)
\]
veya
\[
f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]
Örnekler:
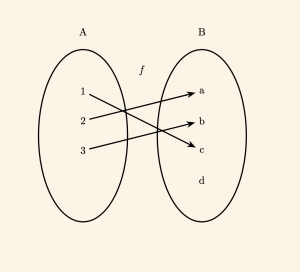
\( \bullet \quad f: A \to B \) fonksiyonu, A’nın her elemanının görüntüsü farklı olduğundan bire birdir. Ayrıca B’de boşta eleman kaldığından bire bir ve içinedir.
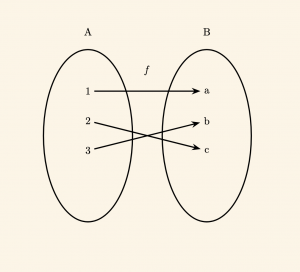
\( \bullet \quad f: A \to B \) fonksiyonu, bire bir ve örtendir.
\( \bullet \quad f: \mathbb{N} \to \mathbb{Z} \), \( f(x) = 2x^3 – 7 \) fonksiyonu,
\[
f(x_1) = 2x_1^3 – 7 \quad \text{ve} \quad f(x_2) = 2x_2^3 – 7
\]
\[
f(x_1) = f(x_2) \Rightarrow 2x_1^3 – 7 = 2x_2^3 – 7
\]
\[
\Rightarrow x_1 = x_2 \quad \text{olduğundan bire birdir.}
\]
\(\bullet \quad f: \mathbb{R} \to \mathbb{R}, \quad f(x) = 2x^2 + 1 \) fonksiyonu,
\[
f(x_1) = 2x_1^2 + 1 \quad \text{ve} \quad f(x_2) = 2x_2^2 + 1
\]
\[
f(x_1) = f(x_2) \Rightarrow 2x_1^2 + 1 = 2x_2^2 + 1
\]
\[
\Rightarrow x_1^2 = x_2^2 \Rightarrow x_1 = \pm x_2
\]
olduğundan bire bir değildir.
\( \bullet \quad f: \mathbb{N} \to \mathbb{N}, \quad f(x) = x^2 + x + 1 \) fonksiyonu,
\[
f(x_1) = x_1^2 + x_1 + 1 \quad \text{ve} \quad f(x_2) = x_2^2 + x_2 + 1
\]
\[
f(x_1) = f(x_2) \Rightarrow x_1^2 + x_1 + 1 = x_2^2 + x_2 + 1
\]
\[
\Rightarrow x_1^2 – x_2^2 + x_1 – x_2 = 0
\]
\[
\Rightarrow (x_1 – x_2)(x_1 + x_2 + 1) = 0
\]
Burada, \( x \in \mathbb{N} \) olduğundan, \( x_1 + x_2 + 1 \neq 0 \) ve
\[
x_1 – x_2 = 0 \Rightarrow x_1 = x_2
\]
O halde bire birdir.
\( \bullet \quad f: \mathbb{R} – \{-1\} \to \mathbb{R} – \{2\} \),
\[
f(x) = \frac{2x – 1}{x + 1}
\]
fonksiyonu,
\[
f(x_1) = \frac{2x_1 – 1}{x_1 + 1} \quad \text{ve} \quad f(x_2) = \frac{2x_2 – 1}{x_2 + 1}
\]
\[
f(x_1) = f(x_2) \Rightarrow \frac{2x_1 – 1}{x_1 + 1} = \frac{2x_2 – 1}{x_2 + 1}
\]
\[
\Rightarrow 2x_1 x_2 – x_2 + 2x_1 – 1 = 2x_1 x_2 – x_1 + 2x_2 – 1
\]
\[
\Rightarrow 3x_1 = 3x_2 \Rightarrow x_1 = x_2
\]
olduğundan bire birdir.
Uyarı:
Grafiği verilen \( y = f(x) \) şeklindeki bir fonksiyonun değer kümesinin her noktasından \( Oy \) eksenine dikmeler çizilir:
1) Grafiği kesmeyen dikme varsa, \( f \) içine fonksiyondur.
2) Grafiği kesmeyen dikme yoksa, \( f \) örten fonksiyondur.
3) Grafiği kesen dikmelerin her biri grafiği sadece bir noktada kesiyorsa, \( f \) bire bir fonksiyondur.
Örnek:
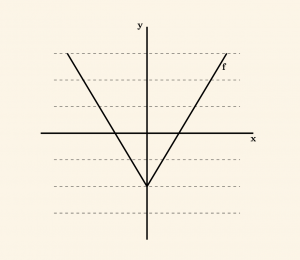
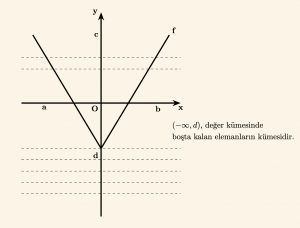
\( f: \mathbb{R} \to \mathbb{R} \) fonksiyonunun grafiği verilmiştir.
\( f \) fonksiyonunun değer kümesi reel sayılar kümesi olduğundan \( Oy \) ekseni üzerindeki her noktadan \( Oy \) eksenine dikmeler çizilir. Grafiği kesmeyen dikmeler olduğundan içine fonksiyondur. Ayrıca grafiği birden fazla (iki) noktada kesen dikmeler olduğundan bire bir fonksiyon değildir.
Burada, grafiği kesmeyen dikmelerin olması, değer kümesinde boşta elemanların bulunması demektir. Grafiği birden fazla noktada kesen dikmelerin olması ise tanım kümesindeki birden fazla elemanın değer kümesinde tek görüntüsünün olması anlamına gelir.
Örnekler:
Aşağıdaki fonksiyonların türlerini belirleyelim.
1)
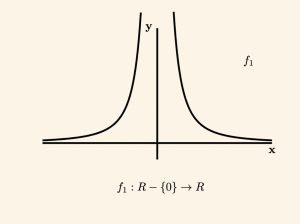
\( f_1\) fonksiyonu, grafiği iki noktada kesen dikmeler olduğundan bire bir deği. Ayrıca grafiği kesmeyen dikme olmadığından örtendir.
2)
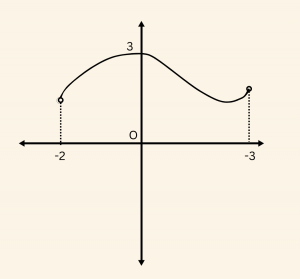 \( f_2\) fonksiyonu, grafiği birden fazla noktada kesen dikmeler olduğundan bire bir degil. Ayrıca grafiği kesmeyen dikmeler olduğundan içinedir.
\( f_2\) fonksiyonu, grafiği birden fazla noktada kesen dikmeler olduğundan bire bir degil. Ayrıca grafiği kesmeyen dikmeler olduğundan içinedir.
3)
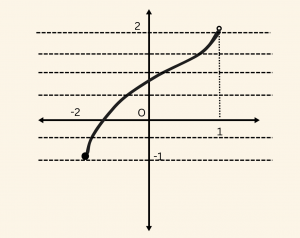
\(f_3 \) fonksiyonu, grafiği kesmeyen dikme olmadığından örtendir. Ayrıca
grafiği birden fazla noktada kesen dikme olmadığından bire birdir.
Bire Bir Fonksiyon Sayısı:
s(A) = m ve s(B) = n olmak üzere,
\( f: A \to B \) bire bir fonksiyonların sayısı:
\[
P(n, m) = \frac{n!}{(n – m)!} \quad (n \geq m)
\]
dir.
\( f: A \to B \) bire bir ve örten bir fonksiyon olması için \( s(A) = s(B) = n \) olmalıdır. O halde,
\( f: A \to B \) bire bir ve örten fonksiyonların sayısı:
\[
\frac{n!}{(n – n)!} = n!
\]
dir.
Örnek:
\( A = \{ 1, 2, 3 \} \) ve \( B = \{ a, b, c, d \} \) ise,
\( f: A \to B \) bire bir fonksiyonların sayısı:
\[
\frac{4!}{(4 – 3)!} = 24
\]
tür.
\( f: A \to A \) bire bir ve örten fonksiyonların sayısı:
\[
3! = 6
\]
dır.
4. Sabit Fonksiyon:
\( f: A \to B \) fonksiyonu verilsin. A’nın her elemanının B’deki görüntüsü aynı ise bu fonksiyona sabit fonksiyon denir.
Yani \(\forall x \in A\) için \( f(x) = c \) ve \( c \in B \) dir.
A’dan B’ye \( s(B) \) tane sabit fonksiyon tanımlanabilir.
Örnek:
\( f: A \to B \) fonksiyonu \( f(x) = c \) şeklinde verilmiştir.
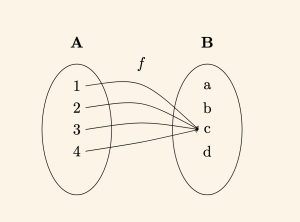
\[
f(1) = c \quad f(2) = c \quad f(3) = c \quad f(4) = c
\]
Burada \( s(B) = 4 \) tane sabit fonksiyon tanımlanabilir.
SORU 20
\( f: \mathbb{R} \to \mathbb{R} \),
\[
f(x) = \frac{(a – 1)x^2 – 3}{ax^2 – 1}
\]
fonksiyonu bir sabit fonksiyon olduğuna göre, \( a \) kaçtır?
\[
\text{A)} -1 \quad
\text{B) } -\frac{1}{2} \quad
\text{C) } 0 \quad
\text{D) } \frac{1}{2} \quad
\text{E) } 1
\]
Çözüm:
\( f \) in bir sabit fonksiyon olması için \( f(x) = c \) ve \( c \in \mathbb{R} \) olmalıdır.
\[
f(x) = \frac{(a – 1)x^2 – 3}{ax^2 – 1} = c
\]
\[
\Rightarrow (a – 1)x^2 – 3 = acx^2 – c
\]
\[
\Rightarrow -3 = -c \quad \text{ve} \quad a – 1 = ac
\]
\[ \Rightarrow c= 3 \quad \text{ve } \quad a-1= 3a\]
\[ \Rightarrow a= -\frac{1}{2} \;\; \text{dir.} \]
\(\textbf{Cevab: B} \)
Sabit Fonksiyonun Grafiği:
\( f: \mathbb{R} \to \mathbb{R}, \;\; f(x) = c \) sabit fonksiyonun grafiği
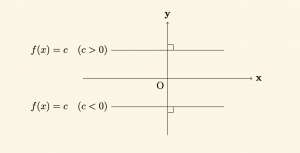
şeklindedir.
Örnek:
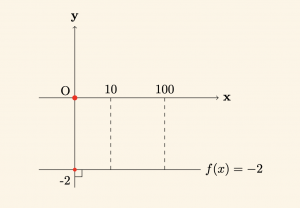
\[
f: \mathbb{R} \to \mathbb{R}, \quad f(x) = -2
\]
sabit fonksiyonunun verilmiştir. \(f(10)= -2 \), \(f(100) = -2 \) dir.
5. Birim Fonksiyon:
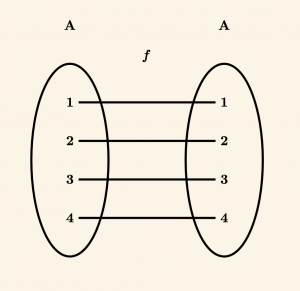
\( f: A \to A \) bir fonksiyon olsun. Tanım kümesindeki her elemanın görüntüsü kendisine eşit ise bu fonksiyona birim fonksiyon denir.
Yani \( \forall x \in A \) için \( f(x) = x \) dir. Birim fonksiyon \( I \) ile gösterilir.
Örnek:
\[
f: A \to A, \quad f(x) = x
\]
\[
f(1) = 1 \quad f(2) = 2 \quad f(3) = 3 \quad f(4) = 4
\]
Birim Fonksiyonun Grafiği:
\( f: \mathbb{R} \to \mathbb{R}, \quad f(x) = x \) birim fonksiyonun grafiği
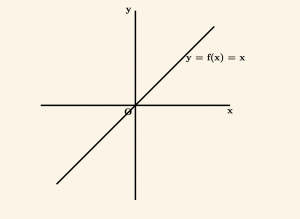
şeklindedir.
6. Bir Fonksiyonun Tersi:
\[
f: A \to B, \quad f = \{ (x, y) \mid x \in A \text{ ve } y \in B \}
\]
bire bir ve örten fonksiyon olmak üzere,
\[
f^{-1}: B \to A, \quad f^{-1} = \{ (y, x) \mid (x, y) \in f \}
\]
fonksiyonuna \( f \)’nin ters fonksiyonu.
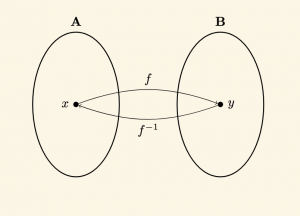
\( (x, y) \in f \Leftrightarrow (y, x) \in f^{-1} \) olduğundan,
\( y = f(x) \Leftrightarrow x = f^{-1}(y) \) dir.
\( f: A \to B \) bire bir ve örten fonksiyon ise,
\( f^{-1}: B \to A \) de bire bir ve örten bir fonksiyondur.
Ayrıca,
\( (f^{-1})^{-1} = f \) dir.
\( f: A \to B \) bire bir ve örten bir fonksiyon değilse,
\( f^{-1} \), \( B \) den \( A \) ya fonksiyon olmayıp, sadece bir bağıntıdır.
Örnek:
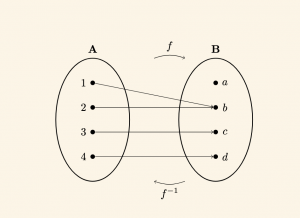
\[ f: A \to B \quad \text{içine fonksiyon, } \quad f^{-1} \quad \text{ise B den A ya bir bağıntıdır.} \]
Örnek:
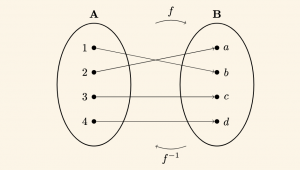
\( f: A \to B \)
\( f = \{ (1, b), (2, a), (3, c), (4, d) \} \) ve
\( f^{-1}: B \to A \)
\( f^{-1} = \{ (b, 1), (a, 2), (c, 3), (d, 4) \} \) dir.
Bir Fonksiyonun Tersinin Bulunuşu:
\( y = f(x) \) şeklindeki bir fonksiyonun tersini bulmak için,
\( y = f(x) \Leftrightarrow x = f^{-1}(y) \) olduğundan,
\( x, y \) cinsinden bulunur ve \( x \) ile \( y \) nin yerleri değiştirilir.
Örnekler:
\( \bullet \quad f: \mathbb{R} \to \mathbb{R}, \quad f(x) = \frac{x – 1}{2} \) ise \( f^{-1}(x) \) i bulalım.
\[
y = f(x) = \frac{x – 1}{2} \Rightarrow x = 2y + 1
\]
\[
\Rightarrow x = f^{-1}(y) = 2y + 1
\]
\[
\Rightarrow f^{-1}(x) = 2x + 1 \quad \text{olur.}
\]
\( \bullet \quad f: \mathbb{R} \to \mathbb{R}, \quad f(x) = x^3 + 1 \) ise \( f^{-1}(x) \) i bulalım.
\[
y = f(x) = x^3 + 1 \Rightarrow x = f^{-1}(y) = \sqrt[3]{y – 1}
\]
\[
\Rightarrow f^{-1}(x) = \sqrt[3]{x – 1} \quad \text{olur.}
\]
\(\bullet \quad f: \mathbb{R} \to \mathbb{R}, \quad f(x) = x^2 \) ise \( f^{-1}(x) \) i bulalım.
\[
y = f(x) = x^2 \Rightarrow x = f^{-1}(y) = \pm \sqrt{y}
\]
\[
\Rightarrow f^{-1}(x) = \pm \sqrt{x} \quad \text{olur.}
\]
Burada \( f \) fonksiyonu bire bir ve örten olmadığından \( f^{-1} \) in fonksiyon olmayıp sadece bir bağıntı olduğu şekilde görülmektedir.
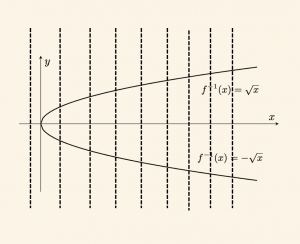
\( \bullet \quad \) Tanım kümesi \( \mathbb{R} – \{3\} \) olan \( f(x) = \frac{-x}{x – 3} \) fonksiyonunun, ters fonksiyonunu ve değer kümesini bulalım.
\[
y = f(x) = \frac{-x}{x – 3} \Rightarrow xy – 3y = x
\]
\[
\Rightarrow xy – x = 3y
\]
\[
\Rightarrow x(y – 1) = 3y
\]
\[
\Rightarrow x = f^{-1}(y) = \frac{3y}{y – 1}
\]
\[
\Rightarrow f^{-1}(x) = \frac{3x}{x – 1}
\]
Bağıntısının fonksiyon olması için, \( x – 1 \neq 0 \Rightarrow x \neq 1 \) olmalıdır. Ayrıca \( f^{-1} \) in tanım kümesi, \( f \) in değer kümesi olup \( \mathbb{R} – \{1\} \) dir.
Uyarı:
\[
f(x) = \frac{ax + b}{cx + d}
\]
bire bir ve örten fonksiyonunda \( a \) ile \( d \) nin yerleri ve işaretleri değiştirilip pratik olarak,
\[
f^{-1}(x) = \frac{-dx + b}{cx – a}
\]
şeklinde bulunur.
Ayrıca \( f(x) = f^{-1}(x) \) olması için \( a = -d \) olmalıdır.
Örnek:
\[
f: \mathbb{R} – \{3\} \to \mathbb{R} – \{2\}, \quad f(x) = \frac{2x – 1}{x – 3}
\]
fonksiyonu verilsin.
\[
f^{-1}(x) = \frac{3x – 1}{x – 2}
\]
dir.
SORU 21
\[
f(x) = \frac{mx + 5}{x – 1}
\]
fonksiyonu bire bir ve örtendir.
\[
f(x) = f^{-1}(x)
\]
olduğuna göre, \( m \) kaçtır?
\[
\text{A)} -1 \quad
\text{B) } 0 \quad
\text{C) } 1 \quad
\text{D) } 2 \quad
\text{E) } 3
\]
Çözüm:
\[
f(x) = f^{-1}(x)
\]
\[
\Rightarrow \frac{mx + 5}{x – 1} = \frac{x + 5}{x – m}
\]
\[
\Rightarrow m = 1 \quad \text{dir.}
\]
\(\textbf{Cevab: C} \)
Uyarı:
\[
y = f(x) = ax^2 + bx + c
\]
şeklindeki fonksiyonların tersini bulurken \( x \) i \( y \) cinsinden bulmak için
\( ax^2 + bx + c \) üç terimlisi tam kareye tamamlanır.
Örnek:
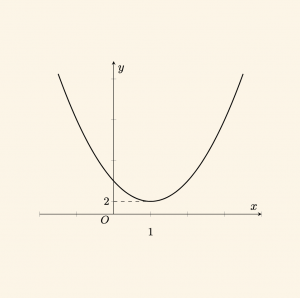
Şekilde grafiği verilen,
\[
f: \mathbb{R} \to \mathbb{R}
\]
\[
f(x) = x^2 – 2x + 3
\]
fonksiyonu bire bir ve örten olmadığından bu fonksiyonun tersi fonksiyon değildir.
Örneğin \( x \geq 1 \) ve \( y \geq 2 \) için \( f \) fonksiyonu bire bir ve örten olup \( f^{-1} \) de fonksiyondur. O halde,
\[
f: [1, \infty) \to [2, \infty), \quad f(x) = x^2 – 2x + 3
\]
için,
\[
y = f(x) = x^2 – 2x + 3
\]
\[
\Rightarrow y = x^2 – 2x + 1 + 2
\]
\[
\Rightarrow y = (x – 1)^2 + 2
\]
\[
\Rightarrow y – 2 = (x – 1)^2
\]
\[
\Rightarrow \sqrt{y – 2} = |x – 1|
\]
\( x \geq 1 \) olduğundan,
\[
\Rightarrow \sqrt{y – 2} = x – 1
\]
\[
\Rightarrow x = f^{-1}(y) = \sqrt{y – 2} + 1
\]
\[
\Rightarrow f^{-1}(x) = \sqrt{x – 2} + 1 \quad \text{olur.}
\]
Uyarı:
\( y = f(x) \) bire bir ve örten bir fonksiyon olsun.
\( f^{-1}(x) \) te bir elemanın görüntüsünü bulmak için, \( f^{-1}(x) \) i bulmaya gerek yoktur.
Örnek:
\[
f(x) = \frac{2x^2 + x + 1}{x^2 + 1}
\]
fonksiyonu verilsin.
Uygun şartlarda \( f^{-1}(2) \) yi bulalım.
\[
x = f^{-1}(y) \Leftrightarrow y = f(x) \quad \text{olduğundan,}
\]
\[
x = f^{-1}(2) \Leftrightarrow 2 = f(x) \quad \text{olacaktır. O halde,}
\]
\[
2 = \frac{2x^2 + x + 1}{x^2 + 1} \Rightarrow 2x^2 + 2 = 2x^2 + x + 1
\]
\[
\Rightarrow x = f^{-1}(2) = 1 \quad \text{dir.}
\]
SORU 22
\( f(x) = x^3 + ax + a \) fonksiyonu veriliyor. Uygun şartlarda \( f^{-1}(5) = 1 \) ise \( a \) kaçtır?
\[
\text{A)} 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[
y = f(x) \Leftrightarrow x = f^{-1}(y) \quad \text{dir.}
\]
O halde,
\[
f^{-1}(5) = 1 \Rightarrow 5 = f(1)
\]
\( f(x) = x^3 + ax + a \) olduğundan,
\[
5 = 1 + a + a
\]
\[
\Rightarrow a = 2 \quad \text{dir.}
\]
\(\textbf{Cevab: B} \)
Ters Fonksiyonun Grafiği:
\( y = f(x) \) fonksiyonun grafiği ile \( y = f^{-1}(x) \) ters fonksiyonunun grafiği
\( y = x \) doğrusuna göre birbirinin simetriğidir.
Örnek:
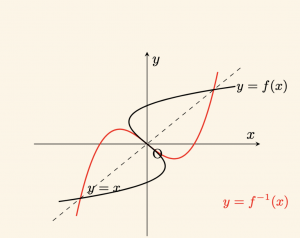
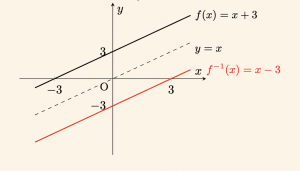
Örnek:
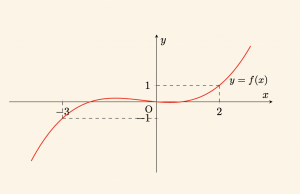
\( f^{-1}(1) + f^{-1}(-1) \quad \text{toplamının değerini bulalım.} \)
\[
y = f(x) \Leftrightarrow x = f^{-1}(y) \quad \text{olduğundan,}
\]
\[
1 = f(2) \Rightarrow 2 = f^{-1}(1)
\]
\[
-1 = f(-3) \Rightarrow -3 = f^{-1}(-1)
\]
\[
f^{-1}(1) + f^{-1}(-1) = 2 – 3 = -1 \quad \text{dir.}
\]
7. Bileşke Fonksiyon:
\[
f: A \to B, \quad g: B \to C
\]
Fonksiyonları verilsin. \( f \) ve \( g \)’yi kullanarak \( A \) kümesinin elemanlarını \( C \) kümesinin elemanlarına eşleyen fonksiyona, \( f \) ile \( g \) nin bileşke fonksiyonu denir.
\[
g \circ f : A \to C, \quad (g \circ f)(x) = g(f(x))
\]
Örnek:
\[
f: \mathbb{R} \to \mathbb{R}, \quad f(x) = x^2 + 1
\]
\[
g: \mathbb{R} \to \mathbb{R}, \quad g(x) = x + 1
\]
\[
(f \circ g)(x) = f(g(x)) = f(x+1) = (x+1)^2 + 1
\]
\[
= x^2 + 2x + 2
\]
\[
(g \circ f)(x) = g(f(x)) = g(x^2 + 1) = (x^2 + 1) + 1
\]
\[
= x^2 + 2
\]
Bileşke Fonksiyonun Özellikleri:
1. Fonksiyonlar arasında tanımlanan bileşke işleminin değişme özelliği yoktur.
\[
f \circ g \neq g \circ f \quad \text{(eğer \( f \neq I \) ve \( g \neq I \) ise)}
\quad (I: \text{ Birim Fonksiyon ) }
\]
Uyarı:
Bazı \( f \) ve \( g \) fonksiyonları için \( f \circ g = g \circ f \) olabilir.
Örnek:
\[
f: \mathbb{R} \to \mathbb{R}, \quad f(x) = x + 2
\]
\[
g: \mathbb{R} \to \mathbb{R}, \quad g(x) = x – 7
\]
\[
(f \circ g)(x) = f(g(x)) = f(x – 7) = x – 7 + 2 = x – 5
\]
\[
(g \circ f)(x) = g(f(x)) = g(x + 2) = x + 2 – 7 = x – 5
\]
Bu durumda:
\[ f \circ g = g \circ f \quad \text{nin olabileceği görülür.} \]
2. Fonksiyonlar arasında tanımlanan bileşke işleminin birleşme özelliği vardır:
\[
f \circ (g \circ h) = (f \circ g) \circ h
\]
\[
f \circ g \circ h = f \circ (g \circ h) = (f \circ g) \circ h
\]
Örnek:
\[
\text{R } \to \text{ R}, \quad f(x) = 2x, \quad g(x) = x^2, \quad h(x) = x + 1
\]
\[
ise
\]
\[
(g \circ h)(x) = g\bigl(h(x)\bigr) = g(x+1) = (x+1)^2
\]
\[
[f \circ (g \circ h)](x) = f\bigl((g \circ h)(x)\bigr)
= f\bigl((x+1)^2\bigr)
= 2(x+1)^2
\]
\[
(f \circ g)(x) = f\bigl(g(x)\bigr)
= f(x^2)
= 2x^2
\]
\[
[(f \circ g) \circ h](x) = (f \circ g)\bigl(h(x)\bigr)
= (f \circ g)(x+1)
= 2(x+1)^2
\]
\[
\text{olduğundan, } f \circ (g \circ h) \;=\; (f \circ g) \circ h \text{ olduğu görülür.}
\]
Uyarı:
\[
(f \circ g \circ h)(x) = [(f \circ g) \circ h](x) = f[g(h(x))]
\]
Örnekler:
\[
\mathbb{R} \to \mathbb{R} \text{ de } f(x) = x^2 – 1 \quad g(x) = 2x, \quad \text{ve} \quad h(x) = x + 2 \text{ ise,}
\]
\( \bullet \quad (fogoh)(x): \)
\[
(f \circ g \circ h)(x) = f[g(h(x))] = \left[ 2(x+2) \right]^2 – 1
\]
\[
= 4x^2 + 16x + 15
\]
\( \bullet \quad (fogoh)(1) \) ifadesini bulalım.
\[
(f \circ g \circ h)(1) = f[g(h(1))]
\]
\[
= f[g(3)]
\]
\[
= f(6) = 35
\]
3. Bileşke fonksiyonun birim fonksiyonla ilişkisi
\[
f \circ I = I \circ f = f, \quad \text{(f: A → A)}
\]
4. Fonksiyonun tersiyle bileşke işlemi
\[
f \circ f^{-1} = f^{-1} \circ f = I, \quad \text{(f: A → A)}
\]
Örnek:
\[
f: \mathbb{R} \to \mathbb{R}, \quad f(x) = \frac{2x – 3}{5}
\]
\[
f^{-1}(x) = \frac{5x + 3}{2}
\]
\[
\Rightarrow (f \circ f^{-1})(x) = f(f^{-1}(x))
\]
\[
= \frac{2 \cdot \left( \frac{5x + 3}{2} \right) – 3}{5} = x \quad \text{olarak bulunur.}
\]
Sonuç:
\[
f \circ f^{-1} = I
\]
Uyarı:
Eğer \( fog = h \) ise \( f \) ve \( g \) fonksiyonlarını bulabiliriz.
1. Her iki tarafın sağından \( g^{-1} \) ile bileşke alırsak:
\[
fog = h \Rightarrow fog \circ g^{-1} = h \circ g^{-1}
\]
\[
\Rightarrow f \circ I = h \circ g^{-1}
\]
\[
\Rightarrow f = h \circ g^{-1}
\]
2. Her iki tarafın solundan \( f^{-1} \) ile bileşke alırsak:
\[
fog = h \Rightarrow f^{-1} \circ fog = f^{-1} \circ h
\]
\[
\Rightarrow I \circ g = f^{-1} \circ h
\]
\[
\Rightarrow g = f^{-1} \circ h
\]
Örnek:
\[
f(x) = \frac{x – 1}{2}, \quad (fog)(x) = 3x + 4 \text{ ise } g(x) \text{ fonksiyonunu bulalım.}
\]
\[
f^{-1}(x) = 2x + 1, \quad h(x) = 3x + 4
\]
\[
g(x) = (f^{-1} \circ h)(x) = f^{-1}(h(x))
\]
\[
= 2(3x + 4) + 1
\]
\[
= 6x + 9
\]
Örnek:
\[
f \left( \frac{2x – 1}{x + 3} \right) = x + 1 \text{ ise } f(x) \text{ fonksiyonunu bulalım.}
\]
\[
g(x) = \frac{2x – 1}{x + 3}, \quad h(x) = x + 1
\]
\[
g^{-1}(x) = \frac{-3x – 1}{x – 2}
\]
\[
f \left( \frac{2x – 1}{x + 3} \right) = x + 1 \Rightarrow (fog)(x) = h(x)
\]
\[
\Rightarrow f(x) = (h \circ g^{-1})(x)
\]
\[
= h(g^{-1}(x))
\]
\[
= \frac{-3x – 1}{x – 2} + 1 = \frac{-2x – 3}{x – 2} \quad \text{olarak bulunur.}
\]
Burada,
\[
f(g(x)) = h(x)
\]
ifadesinde eşitliğin iki yanında \( x \) yerine \( g^{-1}(x) \) yazılarak \( f(x) \) fonksiyonunun bulunduğuna dikkat ediniz.
Örnek:
\[
f \left( \sqrt[3]{x} + 1 \right) = x^2 \text{ ise } f(x) \text{ fonksiyonunu bulalım.}
\]
\[
g(x) = \sqrt[3]{x} + 1 \text{ olsun. } f(x) \text{ i bulmak için eşitliğin her iki yanında } x \text{ yerine } g^{-1}(x) \text{ yazılır.}
\]
Öncelikle \( g^{-1}(x) \) fonksiyonunu bulalım:
\[
y = g(x) = \sqrt[3]{x} + 1 \Rightarrow y – 1 = \sqrt[3]{x}
\]
\[
\Rightarrow (y – 1)^3 = x
\]
\[
\Rightarrow g^{-1}(x) = (x – 1)^3
\]
Şimdi,
\[
f \left( \sqrt[3]{x} + 1 \right) = x^2
\]
eşitliğinde \( x \) yerine \( g^{-1}(x) \) yazarsak:
\[
f \left( \sqrt[3]{(x – 1)^3} + 1 \right) = ((x – 1)^3 + 1)^2
\]
\[
\Rightarrow f(x) = (x – 1)^6 \quad \text{olarak bulunur.}
\]
Uyarı:
Eğer \( f: A \to B \) bire bir ve örten fonksiyon olmak üzere:
\[
A \overset{f}{\longrightarrow}
B \overset{f^{-1}}{\longrightarrow}
A
\quad\quad
B \overset{f^{-1}}{\longrightarrow}
A \overset{f}{\longrightarrow}
B
\]
\[
f^{-1} \circ f = I \quad \text{ve} \quad I : A \to A
\]
\[
f \circ f^{-1} = I \quad \text{ve} \quad I : B \to B
\]
Bunun anlamı:
\[
A \neq B \text{ ve } f: A \to B \; \text{ise } f \circ f^{-1} \neq f^{-1} \circ f
\]
\[
A \neq B \text{ ve } f: A \to A \; \text{ise } f \circ f^{-1} \neq f^{-1} \circ f \quad \text{dir.} \]
Bileşke Fonksiyonun Tersi
Eğer \( f, g, h \) fonksiyonları bire bir ve örten olmak üzere:
\[
(f \circ g)^{-1} = g^{-1} \circ f^{-1}
\]
\[
(f \circ g \circ h)^{-1} = h^{-1} \circ g^{-1} \circ f^{-1}
\]
Örnek:
\[
f(x) = x^2 + 1, \quad g(x) = \frac{-x + 1}{x + 2}
\]
Bu fonksiyonlar bire bir ve örtendir.
\[
(f^{-1} \circ g)^{-1} (2) \text{ ifadesinin değerini bulalım.}
\]
Çözüm:
\[
(f^{-1} \circ g)^{-1} (2) = (g^{-1} \circ (f^{-1})^{-1} )(2)
\]
\[
= (g^{-1} \circ f)(2)
\]
\[
= g^{-1} (f(2))
\]
\[
= g^{-1} (5)
\]
Denklem:
\[
x = g^{-1}(5) \iff 5 = g(x)
\]
\[
\Rightarrow 5 = \frac{-x + 1}{x + 2}
\]
Buradan:
\[
x = g^{-1} (5) = -\frac{3}{2}
\]
olarak bulunur.
SORU 23
\[
f\left( \frac{2x – 1}{3x + 1} \right) = x – 1
\]
olduğuna göre, \( f(3) \) kaçtır?
\[
\text{A)} 1 \quad
\text{B) } – \frac{11}{7} \quad
\text{C) } \frac{11}{7} \quad
\text{D) } -\frac{9}{4} \quad
\text{E) } \frac{9}{4}
\]
Çözüm:
\[
\frac{2x – 1}{3x + 1} = 3
\]
Buradan \( x \) değeri:
\[
x = -\frac{4}{7}
\]
eşitliğin iki yanında \( x \) yerine \( -\frac{4}{7} \) yazarsak:
\[
f\left( \frac{2x – 1}{3x + 1} \right) = x – 1 \Rightarrow f(3) = -\frac{4}{7} – 1
\]
\[
f(3) = -\frac{4}{7} – \frac{7}{7} = -\frac{11}{7}
\]
\(\textbf{Cevab: B} \)
SORU 24
\[
f(x) = \frac{2 f(x-2) + x}{3} \quad \text{ve } f(6) = \frac{16}{3} \quad \text{ise } \; f(2) \; \text{kaçtır?} \]
\[
\text{A)} \frac{11}{2} \quad
\text{B) } \frac{11}{3} \quad
\text{C) } \frac{11}{4} \quad
\text{D) } \frac{11}{5} \quad
\text{E) } \frac{11}{6}
\]
Çözüm:
\[ f(x) = \frac{2f(x-2) + x}{3} \Rightarrow f(6) = \frac{2f(6-2) + 6}{3} \]
\[ \Rightarrow \frac{16}{3} = \frac{2f(4) + 6}{3} \]
\[ \Rightarrow f(4) = 5 \quad \text{Aynı şekilde,} \]
\[ f(x) = \frac{2f(x-2) + x}{3} \Rightarrow f(4) = \frac{2f(4-2) + 4}{3} \]
\[ \Rightarrow 5 = \frac{2f(2) + 4}{3} \]
\[ \Rightarrow f(2) = \frac{11}{2} \quad \text{dir. } \]
\(\textbf{Cevab: A } \)
SORU 25
\( f(x) = 2^{x-2} + 1 \) olduğuna göre, \( f(x+2) \) nin \( f(x) \) cinsinden eşiti aşağıdakilerden hangisidir?
\[
\text{A)} 3f(x) – 1 \quad
\text{B) } 4f(x) – 1 \quad
\text{C) } 4f(x) \quad
\text{D) } 3f(x) \quad
\text{E) } 4f(x) – 3
\]
Çözüm:
\[ f(x) = 2^{x-2} + 1 \Rightarrow f(x+2) = 2^{x+2-2} + 1 \]
\[ \Rightarrow f(x+2) = 2^x + 1 \]
\[ f(x) = 2^{x-2} + 1 \Rightarrow f(x) – 1 = 2^{x-2} \]
\[ \Rightarrow f(x) – 1 = \frac{2^x}{2^2} \]
\[ \Rightarrow 4f(x) – 4 = 2^x \quad \text{olduğuna göre,} \]
\[ f(x+2) = 2^x + 1 = 4f(x) – 4 + 1 \]
\[ = 4f(x) – 3 \quad \text{tür} \]
\(\textbf{Cevab: E} \)
SORU 26
\( f(x^2 + x + 1) = 3x^2 + 3x + 1 \) olduğuna göre, \( f(x) \) aşağıdakilerden hangisidir?
\[
\text{A)} x+1 \quad
\text{B) } 2x+3 \quad
\text{C) } 2x-3 \quad
\text{D) } 3x-2 \quad
\text{E) } 3x+2
\]
Çözüm:
\[
f(x^2 + x + 1) = 3x^2 + 3x + 1
\]
şeklindedir. Burada \( f(x) \) fonksiyonunun genel formunu bulmaya çalışacağız.
Adım 1: Değişken Dönüşümü: Fonksiyonun içine basit bir ifade koyarak \( f(x) \) hakkında bilgi edinmeye çalışalım. Öncelikle \( x = 0 \) için fonksiyon eşitliğine bakalım:
\[
f(0^2 + 0 + 1) = 3(0)^2 + 3(0) + 1
\]
\[
f(1) = 1
\]
Şimdi \( x = 1 \) için eşitliği yazalım:
\[
f(1^2 + 1 + 1) = 3(1)^2 + 3(1) + 1
\]
\[
f(3) = 3 + 3 + 1 = 7
\]
\( x = 2 \) için deneyelim:
\[
f(2^2 + 2 + 1) = 3(2)^2 + 3(2) + 1
\]
\[
f(7) = 3(4) + 6 + 1 = 19
\]
Şimdi \( f(x) \) fonksiyonunun bir doğrusal fonksiyon olup olmadığını kontrol edelim.
Adım 2: Doğrusal Fonksiyon Hipotezi
\( f(x) = ax + b \) şeklinde bir fonksiyon olduğunu varsayalım.
\( f(1) = 1 \) ve \( f(3) = 7 \) verildiğine göre:
\[
a(1) + b = 1
\]
\[
a(3) + b = 7
\]
Bu iki denklemden:
1. \( a + b = 1 \)
2. \( 3a + b = 7 \)
Bu iki denklemden birini diğerinden çıkaralım:
\[
(3a + b) – (a + b) = 7 – 1
\]
\[
2a = 6
\]
\[
a = 3
\]
Bulduğumuz \( a \) değerini birinci denklemde yerine koyarsak:
\[
3 + b = 1
\]
\[
b = -2
\]
\[
f(x) = 3x – 2
\]
II. Yol
\[
\Rightarrow f(x^2 + x + 1) = 3x^2 + 3x + 3 – 2
\]
\[
\Rightarrow f\underbrace {(x^2 + x + 1) }_{a}= 3 \underbrace{(x^2 + x + 1)}_{a} – 2
\]
\[
\Rightarrow f(a) = 3a – 2 \Rightarrow f(x) = 3x – 2 \text{ dir.}
\]
\(\textbf{Cevab: D} \)
SORU 27
\[
f\left( \frac{x}{x^2 + 1} \right) = x – 1
\]
olduğuna göre, \( f^{-1}(x) \) aşağıdakilerden hangisine eşittir?
\[
\text{A) } x \quad
\text{B) } \frac{x+1}{x^2 + 1} \quad
\text{C) } \frac{x}{x^2 + 2} \quad
\text{D) } \frac{x}{x+2} \quad
\text{E) } \frac{x+1}{(x+1)^2 + 1}
\]
Çözüm:
\[
y = f(x) \Leftrightarrow x = f^{-1}(y)
\]
\[
f\left( \frac{x}{x^2 + 1} \right) = x – 1 \Rightarrow \frac{x}{x^2 + 1} = f^{-1}(x – 1)
\]
\[
\Rightarrow \frac{x+1}{(x+1)^2 + 1} = f^{-1}(x + 1 – 1)
\]
\[
\Rightarrow \frac{x+1}{(x+1)^2 + 1} = f^{-1}(x)
\]
olarak bulunur.
\(\textbf{Cevab: E} \)
SORU 28
\[
f(x+1) = 5x^2 + 1 \quad \text{ve} \quad g(x+8) = x^2 + 1
\]
olduğuna göre, \( (gof)(-1) \) kaçtır?
\[
\text{A) } 169 \quad
\text{B) } 170 \quad
\text{C) }171 \quad
\text{D) } 172\quad
\text{E) } 173
\]
Çözüm:
\[
(gof)(-1) = g(f(x)) = g(f(-1))
\]
\[
f(x+1) = 5x^2 + 1 \Rightarrow f(-2+1) = 5(-2)^2 + 1
\]
\[
\Rightarrow f(-1) = 21 \text{ olduğuna göre,}
\]
\[
g(f(-1)) = g(21)
\]
\[
g(x+8) = x^2 + 1 \Rightarrow g(13+8) = (13)^2 + 1
\]
\[
\Rightarrow g(21) = 170 \text{ dir.}
\]
\(\textbf{Cevab: B} \)
SORU 29
\[
f(x) = 2^{x+2} \quad \text{ve} \quad g(x) = x^2 + 15
\]
olduğuna göre, \( (f^{-1} \circ g \circ f)(-2) \) kaçtır?
\[
\text{A) } 2 \quad
\text{B) } 3 \quad
\text{C) }4 \quad
\text{D) } 5\quad
\text{E) } 6
\]
Çözüm:
\[
(f^{-1} \circ g \circ f)(-2) = f^{-1} \left[g(f(x))\right]= f^{-1} \left[g(f(-2))\right]
\]
\[ f(-2) = 2^{x+2}= 2^{-2+2}=2^0= 1\]
\[ g(x) = x^2 + 15 \Rightarrow g(1) = 1^2+15 =16 \]
\[
= f^{-1} (g(1))
\]
\[
= f^{-1} (16) \quad \text{çünkü} \quad 16 = f(x)
\]
\[
\Rightarrow 16 = 2^{x+2}
\]
\[
\Rightarrow x = 2 \text{ olur.}
\]
O halde \( (f^{-1} \circ g \circ f)(-2) = 2 \) dir.
\(\textbf{Cevab: A} \)
SORU 30
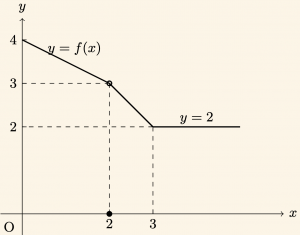
Yukarıdaki şekilde \( y = f(x) \) fonksiyonunun grafiği verilmiştir. \( (fofofof)(5) \) kaçtır?
\[
\text{A) } 6 \quad
\text{B) } 5 \quad
\text{C) }4 \quad
\text{D) } 3\quad
\text{E) } 2
\]
Çözüm:
\( x \geq 3 \) için \( f(x) \) sabit fonksiyon olduğundan,
\[
f(5) = 2 \text{ olup,}
\]
\[
(fofofof)(5) = f[f(f[f(5)])]
\]
\[
= f[f(f(2))]
\]
\[
= f[f(0)]
\]
\[
= f(4) = 2 \text{ dir.}
\]
\(\textbf{Cevab: E} \)
SORU 31
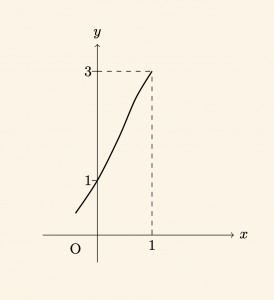
Şekilde \( y = f(x) \) fonksiyonunun grafiği verilmiştir.
\[
(fof)(2x – 4) = 3
\]
olduğuna göre, \( x \) kaçtır?
\[
\text{A) } 0 \quad
\text{B) } 1 \quad
\text{C) }2 \quad
\text{D) } 3\quad
\text{E) } 4
\]
Çözüm:
\[
(fof)(2x – 4) = 3 \Rightarrow f(f(2x – 4)) = 3
\]
Grafikten,
\[
f(1) = 3 \quad \text{olduğundan,} \;\; \Rightarrow f(2x – 4) = 1
\]
\[
f(0) = 1 \quad \text{olduğundan,} \;\; \Rightarrow 2x – 4 = 0
\]
\[
x= 2 \quad \text{bulunur. }
\]
\(\textbf{Cevab: C} \)
8. Permütasyon Fonksiyon:
A sonlu (sayılabilir elemanlı) bir küme olsun. \( f: A \to A \) bire bir her fonksiyona A’nın bir permütasyonu denir.
\( f: A \to A \) bire bir fonksiyonunun tanım kümesi ile değer kümesi birbirinin aynısı olduğundan bu fonksiyon örtendir.
Örnek:
\( A = \{ 1, 2, 3, 4 \} \) olmak üzere, A’nın bir permütasyonu
\[
f =
\begin{pmatrix}
1 & 2 & 3 & 4 \\
3 & 1 & 2 & 4
\end{pmatrix}
\]
şeklinde olsun.
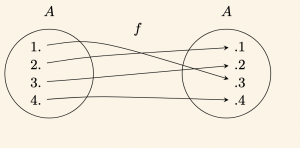
\( f: A \to A \) bire bir ve örten fonksiyondur.
Burada,
\[
\begin{array}{c@{\quad}l}
f =
\begin{pmatrix}
1 & 2 & 3 & 4 \\
3 & 1 & 2 & 4
\end{pmatrix}
&
\begin{aligned}
&\rightarrow \text{tanım kümesi}\\
&\rightarrow \text{değer kümesi}
\end{aligned}
\end{array}
\]
\( f(1) = 3,\quad f(2) = 1,\quad f(3) = 2,\quad f(4) = 4 \) tür.
Ters fonksiyon ise,
\[
f =
\begin{pmatrix}
1 & 2 & 3 & 4 \\
3 & 1 & 2 & 4
\end{pmatrix}
\quad \text{olduğundan,}
\]
\[
f^{-1} =
\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 3 & 1 & 4
\end{pmatrix}
\quad \text{şeklindedir.}
\]
Örnek:
\( A = \{ 1, 2, 3, 4 \} \) kümesinin,
\[
f =
\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 4 & 3 & 1
\end{pmatrix}
\quad\text{ve}\quad
g =
\begin{pmatrix}
1 & 2 & 3 & 4 \\
4 & 3 & 1 & 2
\end{pmatrix}
\]
permütasyonları veriliyor. \(f \circ g^{-1}\) permütasyonunu bulalım.
\[
g^{-1} =
\begin{pmatrix}
1 & 2 & 3 & 4 \\
3 & 4 & 2 & 1
\end{pmatrix}
\]
\[
(f \circ g^{-1})(1) = f\bigl(g^{-1}(1)\bigr)
\quad\text{için}\quad
g^{-1}(1) = 3
\quad\Rightarrow\quad
f(3) = 3
\]
\[
(f \circ g^{-1})(2) = f\bigl(g^{-1}(2)\bigr)
\quad\text{için}\quad
g^{-1}(2) = 4
\quad\Rightarrow\quad
f(4) = 1
\]
\[
(f \circ g^{-1})(3) = f\bigl(g^{-1}(3)\bigr)
\quad\text{için}\quad
g^{-1}(3) = 2
\quad\Rightarrow\quad
f(2) = 4
\]
\[
(f \circ g^{-1})(4) = f\bigl(g^{-1}(4)\bigr)
\quad\text{için}\quad
g^{-1}(4) = 1
\quad\Rightarrow\quad
f(1) = 2
\]
O hâlde,
\[
f \circ g^{-1} =
\begin{pmatrix}
1 & 2 & 3 & 4 \\
3 & 1 & 4 & 2
\end{pmatrix}
\]
olarak bulunur.
Örnek:
\( A = \{ a, b, c \} \) kümesinde,
\[
f =
\begin{pmatrix}
a & b & c \\
c & a & b
\end{pmatrix},
\quad
g \circ f =
\begin{pmatrix}
a & b & c \\
b & a & c
\end{pmatrix}
\]
veriliyor.
\(g\) permütasyonunu bulalım.
\[
f(a) = c
\quad\text{ve}\quad
g\bigl(f(a)\bigr) = b
\quad\Rightarrow\quad
g(c) = b
\]
\[
f(b) = a
\quad\text{ve}\quad
g\bigl(f(b)\bigr) = a
\quad\Rightarrow\quad
g(a) = a
\]
\[
f(c) = b
\quad\text{ve}\quad
g\bigl(f(c)\bigr) = c
\quad\Rightarrow\quad
g(b) = c
\]
olduğuna göre,
\[
g =
\begin{pmatrix}
a & b & c \\
a & c & b
\end{pmatrix}
\]
olarak bulunur.
Permütasyon Fonksiyon Sayisi:
\( s(A) = n \) olmak üzere,
\( f : A \to A \) permütasyon (bire bir ve örten) fonksiyon sayısı:
\[ P(n, n) = \frac{n!}{(n-n)!} = n! \quad \text{dir.} \]
SORU 33
\( A = \{1, 2, 3, 4\} \) kümesinde tanımlanan fonksiyonlardan kaç tanesinin ters fonksiyonu yoktur?
\[
\text{A) } 200 \quad
\text{B) } 232 \quad
\text{C) } 256 \quad
\text{D) } 276 \quad
\text{E) } 278
\]
Çözüm:
\( f : A \to A \) fonksiyon sayısı: \( 4^4 = 256 \),
\( f : A \to A \) ters fonksiyonu olan, yani permütasyon (bire bir ve örten) fonksiyon sayısı: \( 4! = 24 \) tanedir.
O hâlde ters fonksiyonu olmayan fonksiyon sayısı: \( 256 – 24 = 232 \) ‘dir.
\(\textbf{Cevab: B} \)
9. Parçalı Fonksiyon:
Tanım aralığının alt aralıklarında farklı birer kuralla tanımlanan her fonksiyona parçalı fonksiyon denir.
Örnek:
\[
f(x) =
\begin{cases}
g(x), & x \le r \ \text{ise},\\
h(x), & x > r \ \text{ise},
\end{cases}
\]
parçalı fonksiyonunda, \(x \le r\) için \(f(x) = g(x)\) ve \(x > r\) için \(f(x) = h(x)\) dir.
Örnek:
\[
f(x) =
\begin{cases}
x^2, & x \le 1 \ \text{ise},\\
x + 1, & 1 < x < 3 \ \text{ise},\\
2x, & x \ge 3 \ \text{ise},
\end{cases}
\]
parçalı fonksiyonu verildiğine göre, \(f(0)\), \(f(2)\) ve \(f(5)\) değerlerini bulalım.
\[
x = 0 \quad\text{için}\quad x \le 1 \quad\text{olduğundan}\quad f(x) = x^2
\quad\Longrightarrow\quad f(0) = 0
\]
\[
x = 2 \quad\text{için}\quad 1 < x < 3
\quad\text{olduğundan}\quad f(x) = x + 1
\quad\Longrightarrow\quad f(2) = 3
\]
\[
x = 5 \quad\text{için}\quad x \ge 3
\quad\text{olduğundan}\quad f(x) = 2x
\quad\Longrightarrow\quad f(5) = 10
\]
olarak bulunur.
Örnek:
\[
f(3x + 1) =
\begin{cases}
2x + 1, & x \ge -\tfrac{1}{3}\ \text{ise},\\
-x + 1, & x < -\tfrac{1}{3}\ \text{ise},
\end{cases}
\]
verildiğine göre, \(f(0)\) ve \(f(x)\) i bulalım.
\(f(0)\) değerini bulmak için eşitliğin her iki yanına da \(x\) yerine \(-\tfrac{1}{3}\) yazılırsa,
\[
f(3x + 1) = 2x + 1 \]
\[f\bigl(3\cdot(-\frac{1}{3}) + 1\bigr) = 2\cdot\bigl(-\frac{1}{3}\bigr) + 1
= \frac{1}{3}\]
\[f(0) = \frac{1}{3}
\ \text{tür.}
\]
\(f(x)\) ifadesini bulmak için eşitliğin her iki yanına da \(x\) yerine \(\tfrac{x – 1}{3}\) yazılırsa,
\[
f\!\Bigl(3\,\bigl(\tfrac{x – 1}{3}\bigr) + 1\Bigr) =
\begin{cases}
2\!\bigl(\frac{x – 1}{3}\bigr) + 1, & \frac{x – 1}{3} \ge -\frac{1}{3},\\
-\!\bigl(\frac{x – 1}{3}\bigr) + 1, & \frac{x – 1}{3} < -\frac{1}{3},
\end{cases}
\]
yani
\[
\begin{cases}
\frac{2x + 1}{3}, & x \ge 0,\\
\frac{-x + 4}{3}, & x < 0,
\end{cases}
\]
olduğundan
\[
f(x) =
\begin{cases}
\dfrac{2x + 1}{3}, & x \ge 0,\\
\dfrac{-x + 4}{3}, & x < 0,
\end{cases}
\]
olarak bulunur.
Örnek:
\[
f(x) =
\begin{cases}
x^2, & x < 0\ \text{ise},\\
1 + x, & x \ge 0\ \text{ise},
\end{cases}
\]
olduğuna göre, \((f \circ f)(x)\) i bulalım.
\(x < 0\) için \(f(x) = x^2\), \(\,(f \circ f)(x) = f\bigl(f(x)\bigr) = f(x^2)\)
\[
x < 0 \;\;\Longrightarrow\;\; x^2 > 0
\quad\Rightarrow\quad
f\bigl(x^2\bigr) = 1 + x^2 \;\text{olur.}
\]
\[
x \ge 0 \;\;\Longrightarrow\;\; f(x) = 1 + x
\quad\text{ve}\quad
(f \circ f)(x) = f\bigl(f(x)\bigr) = f(1 + x).
\]
\[
x \ge 0
\;\;\Longrightarrow\;\;
1 + x \ge 0
\quad\Rightarrow\quad
f(1 + x) = 2 + x
\;\text{olur.}
\]
O hâlde,
\[
(f \circ f)(x) =
\begin{cases}
1 + x^2, & x < 0,\\
2 + x, & x \ge 0,
\end{cases}
\]
olarak bulunur.
Örnek:
\[
f(x) =
\begin{cases}
1 – x, & x < 1\ \text{ise},\\
x^2 + 1, & x \ge 1\ \text{ise},
\end{cases}
\quad\text{ve}\quad
g(x) =
\begin{cases}
x + 1, & x < 0\ \text{ise},\\
1 – x^2, & x \ge 0\ \text{ise}.
\end{cases}
\]
fonksiyonları veriliyor. \((f + g)(x)\) i bulalım.
\[
x < 0
\quad\Longrightarrow\quad
f(x) = 1 – x, \quad g(x) = x + 1
\quad\Rightarrow\quad
(f + g)(x) = 2.
\]
\[
x \ge 1
\quad\Longrightarrow\quad
f(x) = x^2 + 1, \quad g(x) = 1 – x^2
\quad\Rightarrow\quad
(f + g)(x) = 2.
\]
\[
0 \le x < 1
\quad\Longrightarrow\quad
f(x) = 1 – x, \quad g(x) = 1 – x^2
\quad\Rightarrow\quad
(f + g)(x) = 2 – x – x^2.
\]
O hâlde,
\[
(f + g)(x) =
\begin{cases}
2, & x < 0,\\
2 – x – x^2, & 0 \le x < 1,\\
2, & x \ge 1,
\end{cases}
\]
olarak bulunur.
Örnek:
\[
f(x) =
\begin{cases}
2x + 1, & x \le 0\ \\
1 – x, & 0 < x < 2\ \\
1, & x \ge 2\
\end{cases}
\quad \text{ve } \quad
g(x) =
\begin{cases}
2, & x \le -2\ \\
1 – 2x, & x > -2\
\end{cases}
\]
fonksiyonları veriliyor. \(
-1 < x < 0
\quad\Longrightarrow\quad
(f – g)(x) \) i bulalım.
\[
-1 < x < 0
\quad\Longrightarrow\quad
f(x) = 2x + 1 \] \[ g(x) = 1 – 2x
\]
\[(f-g)(x) = f(x) – g(x) = 4x
\quad\text{olarak bulunur.}
\]
Örnek:
\[
f(x) =
\begin{cases}
\sqrt{x} + 1, & x \ge 0 \ \text{ise},\\
x^2, & x < 0 \ \text{ise},
\end{cases}
\]
fonksiyonunun tersini bulalım.
\[
x \ge 0 \quad\Longrightarrow\quad
f: [0,\infty)\to[1,\infty),\
y = f(x) = \sqrt{x} + 1 \]
\[ \Rightarrow
y – 1 = \sqrt{x}
\quad\Longrightarrow\quad
(y – 1)^2 = x = f^{-1}(y).
\]
Dolayısıyla
\[
f^{-1} : [1,\infty) \to [0,\infty),
\quad
f^{-1}(x) = (x – 1)^2.
\]
\[
x < 0 \quad\Longrightarrow\quad
f: (-\infty,0)\to(0,\infty),\
y = f(x) = x^2 \]
\[ \Rightarrow\quad
\sqrt{y} = \sqrt{x^2} = |x|.
\]
Ancak \(x < 0\) olduğundan \(\sqrt{y} = -\,x\), dolayısıyla
\[
-\sqrt{y} = x = f^{-1}(y).
\]
Bu durumda
\[
f^{-1} : (0,\infty) \to (-\infty,0),
\quad
f^{-1}(x) = -\sqrt{x}.
\]
O hâlde
\[
f^{-1}(x) =
\begin{cases}
(x – 1)^2, & x \ge 1 \ \text{ise},\\
-\sqrt{x}, & x > 0 \ \text{ise}.
\end{cases}
\]
Görüldüğü gibi \(f\) fonksiyonu bire bir ve örten olmadığından, \(f^{-1}\) fonksiyon olmayıp sadece bir bağıntıdır.
Örnek:
\[
f(x) =
\begin{cases}
2x, & x \ge 0 \ \text{ise},\\
-x^2,& x < 0 \ \text{ise},
\end{cases}
\]
fonksiyonunun tersini bulalım.
\[
x \ge 0 \Longrightarrow
f: [0,\infty)\to[0,\infty),
y = f(x) = 2x\]
\[
\Rightarrow
\frac{y}{2} = x = f^{-1}(y).
\]
Dolayısıyla
\[
f^{-1}: [0,\infty)\to[0,\infty),
\quad
f^{-1}(x) = \frac{x}{2}.
\]
\[
x < 0 \;\;\Longrightarrow\;\; f : (-\infty,0) \to (-\infty,0),
\quad y = f(x) = -x^2
\quad\Longrightarrow\quad
\sqrt{-y} = \sqrt{x^2} = |x|.
\]
\[
x < 0 \;\;\Longrightarrow\;\; |x| = -\,x
\quad\Longrightarrow\quad
-\sqrt{y} = x = f^{-1}(y).
\]
Dolayısıyla
\[
f^{-1} : (-\infty,0) \to (-\infty,0),
\quad f^{-1}(x) = -\,\sqrt{-x}.
\]
O hâlde,
\[
f^{-1}(x) =
\begin{cases}
\dfrac{x}{2}, & x \ge 0,\\[6pt]
-\sqrt{-x}, & x < 0,
\end{cases}
\]
olarak bulunur.
Görüldüğü gibi \(f\) fonksiyonu bire bir ve örten fonksiyon olduğundan \(f^{-1}\) fonksiyonudur.
Örnek:
\[
f(2 – x) =
\begin{cases}
x + 2, & x \le 0\ \text{ise},\\
-x + 1, & x > 0\ \text{ise},
\end{cases}
\]
veriliyor. \(f(x)\) i bulalım.
\(\Longrightarrow f(x)\) i bulmak için \(x\) yerine \((2 – x)\) yazalım:
\[
f\bigl(2 – (2 – x)\bigr) = f(x).
\]
Buna göre,
\[
f(2 – (2 – x)) =
\begin{cases}
(2 – x) + 2, & 2 – x \le 0 \ \text{ise},\\
-\,(2 – x) + 1, & 2 – x > 0 \ \text{ise}.
\end{cases}
\]
\[
\Longrightarrow
f(x) =
\begin{cases}
4 – x, & x \ge 2,\\
x – 1, & x < 2,
\end{cases}
\]
olarak bulunur.
SORU 34
\[
f(x) =
\begin{cases}
x + 3, & x > 4,\\
2, & x \le 4,
\end{cases}
\qquad
g(x) =
\begin{cases}
x^2, & x > 2,\\
1 – x, & x \le 2.
\end{cases}
\]
Fonksiyonları veriliyor. \((f \circ g \circ f)(4)\) kaçtır?
\[
\text{A) } 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[
(f \circ g \circ f)(4) = f\bigl(g\bigl(f(4)\bigr)\bigr).
\]
\[
x = 4 \le 4
\quad\Longrightarrow\quad
f(4) = 2.
\]
\[
2 \le 2
\quad\Longrightarrow\quad
g(2) = 1 – 2 = -1.
\]
\[
-1 \le 4
\quad\Longrightarrow\quad
f(-1) = 2.
\]
Dolayısıyla
\[
(f \circ g \circ f)(4) = 2.
\]
\(\textbf{Cevab: B} \)
10. Tek ve Çift Fonksiyonlar:
\(\forall x \in A\) için \(-x \in A\) olmak üzere, \(f : A \to \mathbb{R}\) fonksiyonu verilsin.
\(\forall x \in A\) için
\[
f(x) = f(-x)
\]
ise \(f\) fonksiyonuna çift fonksiyon,
\[
f(-x) = -f(x)
\]
ise \(f\) fonksiyonuna tek fonksiyon denir.
Örnek:
\(
\bullet\quad f : \mathbb{R} \to \mathbb{R}, \quad f(x) = x^2 + 2 \quad \text{fonksiyonu,}
\)
\(
\Longrightarrow f(-x) = (-x)^2 + 2 = x^2 + 2 = f(x)
\quad\text{olduğundan çift fonksiyondur.}
\)
\(
\bullet\quad f : \mathbb{R} \to \mathbb{R}, \quad f(x) = |x| + 1 \quad \text{fonksiyonu,}
\)
\(
\Longrightarrow f(-x) = |-x| + 1 = |x| + 1 = f(x)
\quad\text{olduğundan çift fonksiyondur.}
\)
\(
\bullet\quad f : \mathbb{R} \to \mathbb{R}, \quad f(x) = x^4 + x^2 + 1 \quad \text{fonksiyonu,}
\)
\(
\Longrightarrow f(-x) = (-x)^4 + (-x)^2 + 1 = x^4 + x^2 + 1 = f(x)
\quad\text{olduğundan çift fonksiyondur.}
\)
\(
\bullet\quad f : \mathbb{R} \to \mathbb{R}, \quad f(x) = x^3 \quad \text{fonksiyonu,}
\)
\(
\Longrightarrow f(-x) = (-x)^3 = -\,x^3 = -\,f(x)
\quad\text{olduğundan tek fonksiyondur.}
\)
\(
\bullet\quad f : \mathbb{R} \to \mathbb{R}, \quad f(x) = x^4 + x^3 + 1 \quad \text{fonksiyonu,}
\)
\(
\Longrightarrow f(-x) \neq f(x) \quad \text{ve} \quad f(-x) \neq -\,f(x)
\quad\text{olduğundan \(f\) ne çift ne de tek fonksiyondur.}
\)
Uyarı:
\(f\) çift fonksiyonu için, \(f : x \to f(x)\),
\[
f(-x) = f(x)
\quad\Longrightarrow\quad
(x, f(x)) \;\text{ve}\; (-x, f(x))
\]
noktaları bu fonksiyonun grafiğine aittir. Bu noktalar \(Oy\) eksenine göre simetriktir. Dolayısıyla \(f\) çift fonksiyonunun grafiği \(Oy\) eksenine göre simetriktir.
Örnek:
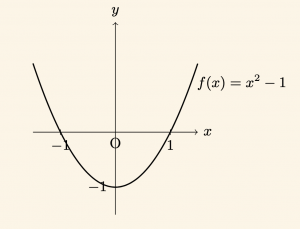
\[
f(x) = x^2 – 1
\]
Grafiği \(y\) eksenine göre simetrik bir paraboldür.
Uyarı:
\(f\) tek fonksiyonu için,
\[f : x \to f(x)\]
\[f: -x \to f(-x) = -\,f(x) \quad \text{olduğundan} \]
\[ \Longrightarrow (x, f(x))\;\text{ve}\;(-x, -f(x)) \]
noktaları bu fonksiyonun grafiğine aittir. Bu noktalar orijine göre simetrik olduğundan \(f\) tek fonksiyonunun grafiği orijine göre simetriktir.
Örnek:
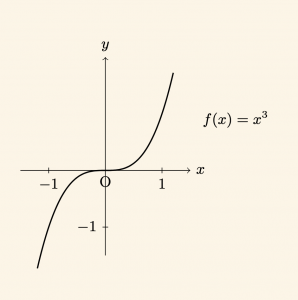
\[
f(x) = x^3
\]
Grafiği orijine göre simetrik bir kubiktir.
← Önceki Sayfa | Sonraki Sayfa →