Fonksiyonlarda Dört İşlem
\( f: A \to \mathbb{R} \) ve \( g: B \to \mathbb{R} \) fonksiyonları verilsin. (\( A \cap B \neq Ø \)) olmak üzere,
1) \[f + g : A \cap B \to \mathbb{R} \quad \text{ve} \quad (f+g)(x) = f(x) + g(x) \]
2) \[ f – g : A \cap B \to \mathbb{R} \quad \text{ve} \quad (f – g)(x) = f(x) – g(x) \]
3) \[ f \cdot g : A \cap B \to \mathbb{R} \quad \text{ve} \quad (f \cdot g)(x) = f(x) \cdot g(x) \]
4) \[ \frac{f}{g} : A \cap B \to \mathbb{R} \quad \text{ve} \quad \left( \frac{f}{g} \right)(x) = \frac{f(x)}{g(x)} \quad g(x) \neq 0 \]
5) \[ c \in \mathbb{R} \quad \text{olmak üzere} \quad c \cdot f : A \to \mathbb{R} \quad \text{ve } \quad (c \cdot f)(x) = c \cdot f(x) \]
Örnekler:
\( f: \mathbb{R} \to \mathbb{R} \) ve \( f(x) = x^2 \),
\( g: \mathbb{R} \to \mathbb{R} \) ve \( g(x) = x^2 + 1 \) fonksiyonları veriliyor.
\( \bullet \quad (2f + g)(x) = 2 f(x) + g(x) = 2x^2 + x^2 + 1 = 3x^2 + 1 \)
\( \bullet \quad { \left( \frac{2g – f}{2} \right)(x)} =\large \frac{2 g(x) – f(x)}{2} \) \(\large= \frac{2 (x^2 + 1) – x^2}{2} = \frac{x^2 + 2}{2}
\)
\( \bullet \quad 1 + x^4 \; -\; (f \cdot g)(x) = 1 + x^4 – f(x) \cdot g(x) \)\(
= 1 + x^4 \;- \; x^2 (x^2 + 1) = 1 \;-\; x^2 \quad \text{olur.}
\)
Soru 10
\( A = \{-1, 0, 1, 2\} \) ve \( B = \{0, 2, 3, 4\} \) kümeleri ile
\( f: A \to \mathbb{R} \), \( f(x) = 2^x \) ve
\( g: B \to \mathbb{R} \), \( g(x) = x^2 \)
fonksiyonları veriliyor.
\[
\frac{2f}{f+g}
\]
fonksiyonunun görüntü kümesi nedir?
\[ \text{A)} \{0, \frac{2}{5} \} \quad \text{B) } \{2,1 \} \quad \text{C) } \{0,2 \} \quad \text{D) } \{0,1 \} \quad \text{E)} \{\frac{2}{5} ,2 \} \]
Çözüm:
\( A \cap B = \{0, 2\} \) olduğuna göre,
\( f(x) = 2^x \Rightarrow \quad f(0) = 2^0 = 1 \quad \) ve \(\quad f(2) = 2^2 = 4 \)
\( g(x) = x^2 \Rightarrow \quad g(0) = 0^2 = 0 \quad \) ve \(\quad g(2) = 2^2 = 4 \)
bulunur.
O halde,
\[
\left(\frac{2f}{f+g}\right)(0) = \frac{2 f(0)}{f(0) + g(0)} = \frac{2 \cdot 1}{1 + 0} = 2
\]
\[
\left(\frac{2f}{f+g}\right)(2) = \frac{2 f(2)}{f(2) + g(2)} = \frac{2 \cdot 4}{4 + 4} = 1
\]
\[
\left(\frac{2f}{f+g}\right)(A \cap B) = \{2, 1\}
\]
olarak bulunur.
\(\textbf{Cevab: B} \)
Soru 11
\( f(x) = x^4 + 4x^3 + 6x^2 + 4x + 1 \) olduğuna göre, \( f(\sqrt{2} – 1) \) kaçtır?
\[ \text{A)} 1 \quad \text{B) } 2 \quad \text{C) } 3 \quad \text{D) } 4 \quad \text{E)} 5 \]
Çözüm:
\[
f(x) = x^4 + 4x^3 + 6x^2 + 4x + 1 = (x+1)^4
\]
\[
f(\sqrt{2} – 1) = (\sqrt{2} – 1 + 1)^4 = (\sqrt{2})^4 = 4 \text{ tür.}
\]
\(\textbf{Cevab: D} \)
Soru 12
\( f: \mathbb{R} \to \mathbb{R} \), \( f(x) = x^2 + x + 1 \) fonksiyonu veriliyor.
\( A = (1,2] \) ve \( f(A) = B \) olduğuna göre, B kümesi aşağıdakilerden hangisidir?
\[ \text{A)} (4,7] \quad \text{B) } (3,6] \quad \text{C) } (1,5] \quad \text{D) } (3,7] \quad \text{E)} (2,8] \]
Çözüm:
\( y = f(x) = x^2 + x + 1 \) ve \( A = (1,2] \) ise, \( A = \{ x \mid 1 < x \leq 2, x \in \mathbb{R} \} \) olduğundan,
\[ 1 < x \leq 2 \quad \Rightarrow \quad 1^2 < x^2 \leq 2^2 \]
\[ = 1 < x^2 \leq 4 \]
\[ 1 < x \leq 2 \quad \Rightarrow \quad 1 + x < x + 1 \leq 2 + 1 \]
\[ = 2 < x + 1 \leq 3 \]
Her iki denklemide toplarsak:
\[
\begin{aligned}
& 1 < x^2 \leq 4 \\
+ \quad & 2 < x + 1 \leq 3\\
\hline \\
&3 < x^2 + x + 1 \leq 7
\end{aligned}
\]
O halde,
\[
B = \{ y \mid 3 < y \leq 7, y \in \mathbb{R} \} \Rightarrow B = (3,7]
\]
\(\textbf{Cevab: D} \)
Soru 13
\[ f: A \to B, \; f(x) = \frac{x+1}{2} \quad \text{ve} \quad B = (-2,1) \] olduğuna göre, A kümesi aşağıdakilerden hangisidir?
\[ \text{A)} (-5,1 ) \quad \text{B) } (-4,2 ) \quad \text{C) } (-3,3) \quad \text{D) } (-2,4 ) \quad \text{E)} (-1,5 ) \]
Çözüm:
\[ y = f(x) = \frac{x+1}{2} \quad \text{ve} \quad B = (-2,1) \quad \text{ise, } \]
\[
B = \{ y \mid -2 < y < 1, y \in \mathbb{R} \} \quad \text{olduğundan,}
\]
\[
-2 < \frac{x+1}{2} < 1
\]
\[
\Rightarrow -2 \cdot 2 < x + 1 < 1 \cdot 2
\]
\[
\Rightarrow -4 – 1 < x < 2 – 1
\]
\[
\Rightarrow -5 < x < 1
\]
O halde,
\[
A = \{ x \mid -5 < x < 1, x \in \mathbb{R} \} \Rightarrow A = (-5,1)
\]
\(\textbf{Cevab: A} \)
Soru 14
\( f: \mathbb{R}^2 \to \mathbb{R} \),
\( f(x, y) = x^3\; -\; y^3\; -\; \; 3xy \cdot (x – y) \) olduğuna göre, \( f(1995, 1996) \) kaçtır?
\[ \text{A)} -1 \quad \text{B) } 0 \quad \text{C) } 1 \quad \text{D) } 2 \quad \text{E )} 3 \]
Çözüm:
\( f \) fonksiyonunun tanım kümesi ikililerden meydana gelmiştir.
Fonksiyon:
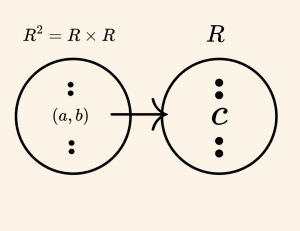
şeklinde gösterilir.
\[
f(x, y) = x^3 \;- \;y^3 \;- \;3xy \cdot (x – y)
\]
\[
= x^3 \;-\; 3x^2 y + 3xy^2\; -\; y^3
\]
\[
\Rightarrow f(x, y) = (x – y)^3
\]
\[
\Rightarrow f(1995, 1996) = (1995 – 1996)^3 = (-1)^3 = -1
\]
\(\textbf{Cevab: A} \)
Soru 15
\( f(x + y) = f(x) \cdot f(y) \) ve \( f(2) = 3 \) olduğuna göre, \( f(8) \) kaçtır?
\[ \text{A)} 3 \quad \text{B) } 9 \quad \text{C) } 27 \quad \text{D) } 81 \quad \text{E )} 243 \]
Çözüm:
\[
f(x + y) = f(x) \cdot f(y)
\]
\[
\Rightarrow f(8) = f(2 + 2 + 2 + 2) = f(2) \cdot f(2) \cdot f(2) \cdot f(2)
\]
\[
= 3 \cdot 3 \cdot 3 \cdot 3 = 81
\]
\(\textbf{Cevab: D} \)
← Önceki Sayfa | Sonraki Sayfa →