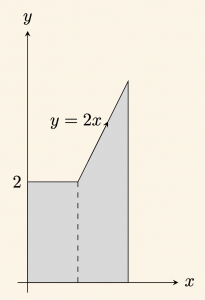
Fonksiyonun Grafiği
Bir fonksiyonun elemanlarına, analitik düzlemde karşılık gelen noktaların kümesine bu fonksiyonun grafiği denir.
\[f: A \to B, \; f= \{ (x,y) \;| ; x \in A , y \in B \quad \text{ve } \quad y= f(x) \} \]
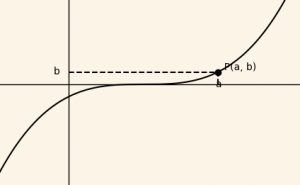
\( (a, b) \in f \) olduğundan \(b = f(a) \) dır.
Soru 16
Şekilde \( y= f(x) \) fonksiyonunun grafiği verilmiştir
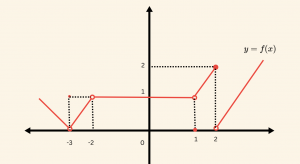
\[ A= \frac{f(-3)+ f(1) }{f(2)} \quad \text{ifadesi kaça eşittir.} \]
\[ \text{A)} 2 \quad \text{B) } 1 \quad \text{C) } \frac{1}{2} \quad \text{D) } -\frac{1}{2} \quad \text{E )} -1 \]
Çözüm:
\[
\begin{aligned}
&f(-3)= 1\\
\\
&f(1)=0 \\
\\
& f(2) =0 \quad \text{olduğundan} \\
\\
& A= \frac{1+0 }{2} = \frac{1}{2}
\end{aligned}
\]
Soru 17
yukarıdaki şekle göre, \(f:x \to ” x\) in solundaki taralı alan” şeklinde bir fonksiyon tanımlanıyor. \( x> 1 \) için \( f(x) \) in eşiti nedir.
\[ \text{A)} x^2 \quad \text{B) } x^2+1 \quad \text{C) } x^2+2 \quad \text{D) } x^2+3 \quad \text{E )} x^2+4 \]
Çözüm:
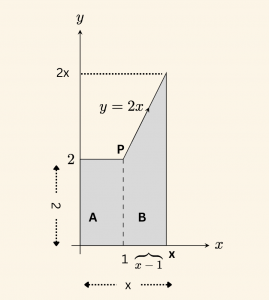
Şekilde, ordinatı \(2 \) olan \( P\) noktası \( z= 2x \) doğrusu üzerinde olduğundan, \(2 = 2x \Rightarrow x= 1 \) olup bu noktanın apsisi \(1 \) dir.
\[ f(x) = \text{Alan (A) } + \text{Alan (B) } \]
\[= 2 + x^2 -1 = x^2+1 \;\; \text{dir. } \]
\(\textbf{Cevab: B} \)