İşlem
\(A\) boş olmayan bir küme ve \(A \subset B\) olsun.
Her
\[
f : A \times A \to B
\]
fonksiyonuna, \(A\) üzerinde bir ikili işlem veya kısaca işlem denir.
İşlemleri genellikle \(+\), \(-\), \(\cdot\), \(\times\), \(\star\), \(\Delta\), \(\circ\), \( \dots \) gibi sembollerle göstereceğiz.
\[
\star : A \times A \to B
\]
işlemi verildiğinde, her \((x, y) \in A \times A\) sıralı ikilisi bir tek \(z \in B\) elemanına eşlenir. Bunu
\[
(x, y)\;\to\;x \,\star\,y \;=\;z
\]
şeklinde gösteririz.
Örnek:

\[
A = \{1, 2\},\quad
B = \{1, 2, 3, 4\}
\]
olmak üzere, \(A \times A\)’dan \(B\)’ye
\[
f(x,y) = x + 2y
\]
bağıntısını inceleyelim.
\[
f(x,y) = x + 2y.
\]
\[
f(1,1) = 1 + 2\cdot1 = 3,\quad
f(1,2) = 1 + 2\cdot2 = 5,\quad
f(2,1) = 2 + 2\cdot1 = 4,\quad
f(2,2) = 2 + 2\cdot2 = 6.
\]
\(f\) bağıntısı \(A \times A\)’dan \(B\)’ye bir fonksiyon değildir. O hâlde \(f\), \(A\) üzerinde bir işlem değildir.
Örnek:
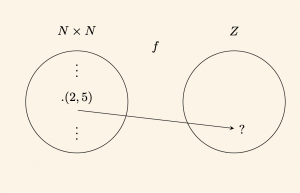
\[
\mathbb{N} \times \mathbb{N}\ \text{den}\ \mathbb{Z}\ \text{ye}\quad
f(x,y) = \frac{x + y}{3}
\]
bağıntısını inceleyelim.
\[
f(x,y) = \frac{x + y}{3}.
\]
Örneğin,
\[
f(2,5) = \frac{2 + 5}{3} = \frac{7}{3},
\]
ki bu değer \(\mathbb{Z}\)’de değildir. Buna göre, \(f\) bağıntısı \(\mathbb{N} \times \mathbb{N}\)’den \(\mathbb{Z}\)’ye bir fonksiyon değildir. O hâlde \(f\), doğal sayılar kümesi üzerinde bir işlem değildir.
Örnek:
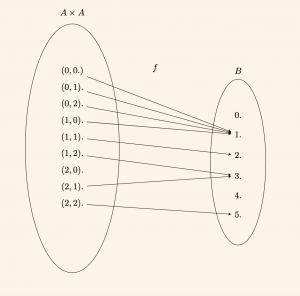
\(A = \{0, 1, 2\}\) ve \(B = \{0, 1, 2, 3, 4, 5\}\) olmak üzere, \(A \times A\)’dan \(B\)’ye
\[
f(x, y) = x \cdot y + 1
\]
bağıntısını inceleyelim.
\(f\) bağıntısı \(A \times A\)’dan \(B\)’ye bir fonksiyondur. O hâlde \(f\), \(A\) kümesi üzerinde bir işlemdir.
\[
f(x, y) = x \cdot y + 1 \]\[
\quad\Rightarrow\quad
\text{Bu işlemi } \star \text{ sembolüyle gösterirsek, }
x \star y = x \cdot y + 1.
\]
Bu işlemin tablosu aşağıdaki gibidir:
\[
\begin{array}{c|ccc}
\star & 0 & 1 & 2\\
\hline
0 & 1 & 1 & 1\\
1 & 1 & 2 & 3\\
2 & 1 & 3 & 5
\end{array}
\]
\[
2 \star 2 = 2 \cdot 2 + 1 = 5
\quad\text{şeklindedir.}
\]
Uyarı:
\(A\) kümesi üzerinde tanımlanan \(\star\) işleminin tablosu aşağıdaki gibi olsun:
\[
\begin{array}{c|cccc}
\star & \dots & b & \dots \to \quad \text{Başlangıç Satırı} \\ \hline
a & & x& \\
\vdots& & & \\
\downarrow \\ \text{başlangıç sütunu }
\end{array}
\]
Yukarıdaki tabloda \((a, b)\) girişine yazılan \(x\) değeri “\(a \star b = x\)” şeklinde okunur.
Örnek:
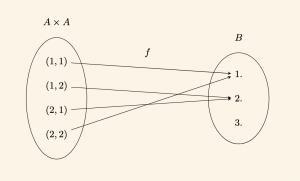 \(A = \{1, 2\},\ B = \{1, 2, 3\}\) olmak üzere, \(A \times A\)’dan \(B\)’ye
\(A = \{1, 2\},\ B = \{1, 2, 3\}\) olmak üzere, \(A \times A\)’dan \(B\)’ye
\[
f(x,y) = 2^{\,|x – y|}\
\]
kuralı ile tanımlı bağıntıyı inceleyelim.
\[ \Longrightarrow f(1,1) = 2^{|1-1|} = 2^0 = 1, \]
\[f(1,2) = 2^{|1-2|} = 2^1 = 2, \]
\[ f(2,1) = 2^{|2-1|} = 2^1 = 2, \]
\[ f(2,2) = 2^0 = 1. \]
\(f\) bağıntısı \(A \times A \to B\) ye bir fonksiyondur. O hâlde \(A\) üzerinde bir işlemdir.
\(f(x,y) = 2^{\,|x-y|}\) kuralı ile verilen işlemi \(\Delta\) sembolü ile gösterelim. Bu işlemin tablosu,
\[
x \,\Delta\, y = 2^{\,|x – y|}
\quad\Rightarrow\quad
\begin{array}{c|cc}
\Delta & 1 & 2 \\
\hline
1 & 1 & 2 \\
2 & 2 & 1
\end{array}
\]
\[
x \,\Delta\, y = 2^{|x – y|}
\]
\[
1 \,\Delta\, 1 = 2^{ |1 – 1| } = 2^0 = 1
\]
\[
1 \,\Delta\, 2 = 2^{|1 – 2|} = 2^1 = 2
\]
\[
2 \,\Delta\, 1 = 2^{|2 – 1|} = 2^1 = 2
\]
\[
2 \,\Delta\, 2 = 2^{|2 – 2|} = 2^0 = 1
\]
şeklindedir.
SORU 1
\(\mathbb{R}\) üzerinde tanımlı \(x \star y = x^y + y^x\) işlemi veriliyor. \((2 \star 3) \star 1\) işleminin sonucu kaçtır?
\[
\text{A) } 14 \quad
\text{B) } 15 \quad
\text{C) } 16\quad
\text{D) } 17 \quad
\text{E) } 18
\]
Çözüm:
\[
x \star y = x^y + y^x
\quad\Longrightarrow\quad
2 \star 3 = 2^3 + 3^2 = 8 + 9 = 17
\]
\[
(2 \star 3) \star 1 = 17 \star 1 = 17^1 + 1^{17} = 17 + 1 = 18
\]
\(\textbf{Cevab: E} \)
SORU 2
\(\mathbb{R}\) üzerinde tanımlı
\[
x \,\Delta\, y =
\begin{cases}
x \cdot y, & x > y \ \text{ise},\\
x + y, & x \le y \ \text{ise},
\end{cases}
\]
işlemi veriliyor. \((2 \,\Delta\, 2)\,\Delta\, 5\) işleminin sonucu kaçtır?
\[
\text{A) } 6 \quad
\text{B) } 7 \quad
\text{C) } 8\quad
\text{D) } 9 \quad
\text{E) } 10
\]
Çözüm:
\(x \le y\) ise \(x \,\Delta\, y = x + y\) olduğuna göre,
\[
2 \,\Delta\, 2 = 2 + 2 = 4
\]
yine \(x \le y\) ise \(x \,\Delta\, y = x + y\) olduğundan,
\[
(2 \,\Delta\, 2)\,\Delta\, 5 = 4 \,\Delta\, 5 = 4 + 5 = 9
\]
\(\textbf{Cevab: D} \)
SORU 3
\( \mathbb{R} – \{0\} \) üzerinde tanımlı \(\star\) işlemi,
\[
\frac{2}{a \star b} \;=\; \frac{2}{a} \;+\; \frac{b}{3}
\]
şeklinde verilmiştir. \(1 \star 6\) işleminin sonucu kaçtır?
\[
\text{A) } \frac{1}{2} \quad
\text{B) } 2 \quad
\text{C) } 3\quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[
\frac{2}{a \star b}
\;=\;
\frac{2}{a} + \frac{b}{3}
\;\Longrightarrow\;
\frac{2}{\,1 \star 6\,}
=
\frac{2}{1} + \frac{6}{3}
= 2 + 2
= 4
\]
\[ 2 = 4 \cdot ( 1 \star 6 ) \]
\[
\Rightarrow \quad 1 \star 6 = \frac{1}{2}
\]
\(\textbf{Cevab: A} \)
SORU 4
\(\mathbb{R}^+\) üzerinde tanımlı \(\Delta\) ile \( \circ\) işlemleri,
\[
9^{x \,\Delta\, y} = x^y
\quad\text{ve}\quad
x \,\circ\, y = (x \,\Delta\, y) + xy + 1
\]
şeklinde verilmiştir. \(3 \circ 4\) işleminin sonucu kaçtır?
\[
\text{A) } 14 \quad
\text{B) } 15 \quad
\text{C) } 16 \quad
\text{D) } 17 \quad
\text{E) } 18
\]
Çözüm:
\[
x \,\circ\, y = (x \,\Delta\, y) + x\,y + 1
\]
\[3 \circ 4 = (3 \,\Delta\, 4) + 3\cdot4 + 1\]
\[3 \circ 4 = (3 \,\Delta\, 4) + 13
\]
O halde \(3 \,\Delta\, 4\)’ü bulalım.
\[9^{x \,\Delta\, y }= x^y \quad\Longrightarrow\quad 9^{3 \,\Delta\, 4} = 3^4\]
\[= 9^{3 \,\Delta\, 4} = 9^2\]
\[\Rightarrow 3 \,\Delta\, 4 = 2\]
Bu değeri yerine yazarsak,
\[
3 \circ 4 = (3 \,\Delta\, 4) + 13 = 2 + 13 = 15
\]
\(\textbf{Cevab: B} \)
SORU 5
\(\mathbb{R}\) üzerinde tanımlı \(\star\) işlemi,
\[
\sqrt[3]{x} \;\star\; \sqrt[3]{y} \;=\; x^2 + y^2
\]
şeklinde verilmiştir. \(-1 \;\star\; 2\) işleminin sonucu kaçtır?
\[
\text{A) } 63 \quad
\text{B) } 64 \quad
\text{C) } 65 \quad
\text{D) } 66 \quad
\text{E) } 67
\]
Çözüm:
\[
\sqrt[3]{x} \;\star\; \sqrt[3]{y} \;=\; x^2 + y^2
\]
\[ x \;\to\; (-1)^3 = -1,
\quad \text{ve } \quad
y \to\; 2^3 = 8.
\]
\[
\sqrt[3]{-1} \;\star\; \sqrt[3]{8}
= (-1) \;\star\; 2
= (-1)^2 + 8^2 = 1 + 64 = 65.
\]
\(\textbf{Cevab: C} \)
SORU 6
\(\mathbb{R} – \{0\}\) üzerinde tanımlanan \(\star\) işlemi,
\[
\frac{2}{x} \;\star\; \frac{3}{y} \;=\; x + y
\]
şeklinde verilmiştir. \(x \;\star\; y\) işlemi aşağıdakilerden hangisidir?
\[
\text{A) } \frac{2x+ 3y}{xy} \quad
\text{B) } \frac{3x+ y}{xy} \quad
\text{C) } \frac{2x+ y}{xy} \quad
\text{D) } \frac{x+ y}{xy} \quad
\text{E) } \frac{2y+ 3x}{xy}
\]
Çözüm:
Önce \(a \;\star\; b\) yi bulalım.
\[
\frac{2}{x} \;\star\; \frac{3}{y} = x + y
\]
\[\frac{2}{x} = a
\;\Rightarrow\;
x = \frac{2}{a},
\quad
\frac{3}{y} = b
\;\Rightarrow\;
y = \frac{3}{b}.
\]
\[
\frac{2}{\frac{2}{a} } \;\star\; \frac{3}{\frac{3}{b} }
= \frac{2}{a} + \frac{3}{b}
= \frac{2b + 3a}{ab}\]
\[
a \;\star\; b = \frac{2b + 3a}{ab}.
\]
Burada \(a\) yerine \(x\), \(b\) yerine \(y\) yazılırsa,
\[
x \;\star\; y
= \frac{2y + 3x}{\,x\,y}.
\]
\(\textbf{Cevab: E} \)
SORU 7
\(\mathbb{R}^2\) üzerinde \(o\) işlemi,
\[
(x, y)\, o\, (z, t) = \bigl(x \cdot z,\; x + y + t + 1\bigr)
\]
şeklinde tanımlanmıştır.
\[
(m, n) \, o \, (2, 3) = (4, 7)
\quad\text{ise}\quad
m \cdot n \text{ kaçtır?}
\]
\[
\text{A) } 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[
(x, y)\, o\, (z, t)
= (x \cdot z,\; x + y + t + 1).
\]
\[
(m, n)\, o\, (2, 3)
= (\,m \cdot 2,\; m + n + 3 + 1\,)
= (4, 7).
\]
Buna göre,
\[
m \cdot 2 = 4
\quad\Longrightarrow\quad
m = 2,
\]
ve
\[
m + n + 4 = 7
\quad\Longrightarrow\quad
2 + n + 4 = 7
\quad\Longrightarrow\quad
n = 1.
\]
Dolayısıyla
\[
m \cdot n = 2 \cdot 1 = 2.
\]
\(\textbf{Cevab: B} \)
← Önceki Sayfa | Sonraki Sayfa →