İşlemin Özellikleri

1. Kapalılık Özelliği:

A kümesi üzerinde bir $ \star $ işlemi tanımlansın.

$ \star, A \times A $ dan $ A $ ya bir fonksiyon ise A kümesi $ \star $ işlemine göre kapalıdır denir. Bu durumda,

\[\forall x, y \in A \quad \text{için} \quad x \star y \in A \]

olur.

İşlem tablosu oluşturulduğunda tablodaki tüm elemanlar A ya ait ise A kümesi bu işleme göre kapalıdır. İşlem tablosunda A ya ait olmayan eleman varsa, A kümesi bu işleme göre kapalı değildir.

Örnek:

$ A = \{ 1, 2 \} $ kümesi üzerinde $ x \star y = y^x $ şeklinde bir $ \star $ işlemi tanımlansın. Bu işlemin kapalılık özelliğini inceleyelim.

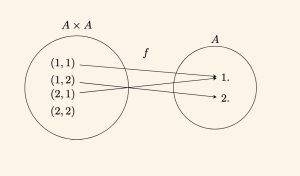$ f(x, y) = x \star y = y^x $

$ 1 \star 1 = 1^1 = 1 \in A $

$ 1 \star 2 = 2^1 = 2 \in A $

$ 2 \star 1 = 1^2 = 1 \in A $

$ 2 \star 2 = 2^2 = 4 \notin A $

Burada $ f $ bağıntısı $ A \times A $ dan $ A $ ya fonksiyon olmadığından $ A $ kümesi $\star$ işlemine göre kapalı değildir. Ayrıca tabloda $ A $ ya ait olmayan eleman (4) olduğundan $ A $ kümesinin $\star$ işlemine göre kapalı olmadığı görülebilir.

\[
\begin{array}{c|cccc}
\star & 1 & 2 &\\
\hline
1 & 1 & 2 \\
2 & 1 & 4 \\
\end{array}
\]

Örnek:

$ N $ üzerinde tanımlanan \[ x \star y = \frac{x \cdot y + 1}{3} \] işleminin kapalılık özelliğini inceleyelim.

Örneğin $ 1 $ ve $ 4 \in N $ için $ 1 \star 4 = \frac{1 \cdot 4 + 1}{3} = \frac{5}{3} \notin N $ olduğundan $ N $ kümesi $\star$ işlemine göre kapalı değildir.

Örnek:

$ Z $ üzerinde tanımlanan
\[ x \circ y = x^2 + y^2 \]
işleminin kapalılık özelliğini inceleyelim.

$\forall x, y \in Z$ için $ x \circ y \in Z $ olduğundan $ Z $ kümesi $\circ$ işlemine göre kapalıdır.

2. Değişme Özelliği:

$ A $ kümesi üzerinde bir $\star$ işlemi tanımlansın. $\forall x, y \in A$ için $ x \star y = y \star x $
ise $\star$ işleminin değişme özelliği vardır. İşlem tablosu oluşturulduğunda işlem tablosu köşegene göre simetrik ise bu işlemin değişme özelliği vardır.

Örnek:

$ \mathbb{R} $ üzerinde
\[ a \star b = ab + a + b + 1 \]
şeklinde tanımlanan $\star$ işleminin değişme özelliğini inceleyelim.

\[ x \star y = xy + x + y + 1 \] ve \[ y \star x = yx + y + x + 1 \] olduğundan \[ x \star y = y \star x \] O halde işlemin değişme özelliği vardır.

Örnek:

$ \mathbb{R} $ üzerinde
\[ a \circ b = \frac{ab}{a^2 + b^2} \]
şeklinde tanımlanan $ o $ işleminin değişme özelliğini inceleyelim.

\[ x \circ y = \frac{xy}{x^2 + y^2} \] ve
\[ y \circ x = \frac{yx}{y^2 + x^2} \]
olduğundan $ x \circ y = y \circ x $’tir. O halde $ o $ işleminin değişme özelliği vardır.

Örnek:

$ \mathbb{R}^2 $ üzerinde
\[ (a, b) \circ (c, d) = (2ac,\, 2b + d) \]
şeklinde tanımlanan $ o $ işleminin değişme özelliğini inceleyelim.

\[ (x, y) \circ (z, t) = (2xz,\, 2y + t) \] ve
\[ (z, t) \circ (x, y) = (2zx,\, 2t + y) \]
olduğundan $ (x, y) \circ (z, t) \neq (z, t) \circ (x, y) $. O halde $ o $ işleminin değişme özelliği yoktur.

Örnek

\[
\begin{array}{c|cccc}
\star & a & b & c & d\\
\hline
a & c & d & a & b \\
b & d & a & b & c \\
c & a & b & c & d \\
d & b & c & d & a
\end{array}
\]
$\star$ işleminin tablosu köşegene göre simetrik olduğundan değişme özelliği vardır.

\[
\begin{array}{c|cccc}
o & 1 & 2 & 3 & 4\\
\hline
1 & 1 & 2 & 3 & 4 \\
2 & 2 & 3 & 4 & 1 \\
3 & 3 & 4 & 1 & 2 \\
4 & 4 & 1 & 1 & 3
\end{array}
\]
$ o $ işleminin tablosu köşegene göre simetrik olmadığından değişme özelliği yoktur.

3. Birleşme Özelliği:

$ A $ kümesi üzerinde bir $\star$ işlemi tanımlansın. $\forall x, y, z \in A$ için
\[ x \star y \star z = x \star (y \star z) = (x \star y) \star z \] ise $\star$ işleminin birleşme özelliği vardır.

Örnek:

$ \mathbb{R} $ üzerinde
\[ a \circ b = a + b + 3 \]
şeklinde tanımlanan $ o $ işleminin birleşme özelliğini inceleyelim.

\[ x \circ (y \circ z) = x + (y + z + 3) + 3 = x + y + z + 6 \]
\[(x \circ y) \circ z = (x + y + 3) + z + 3 = x + y + z + 6 \]
Dolayısıyla $ x \circ (y \circ z) = (x \circ y) \circ z $. O halde $ o $ işleminin birleşme özelliği vardır.

Örnek:

$\mathbb{R}$ üzerinde $a \circ b = ab + 3$ şeklinde tanımlanan $\circ$ işleminin birleşme özelliğini inceleyelim.

\[
x \circ (y \circ z) = x(y \circ z) + 3
= x(yz + 3) + 3
= xyz + 3x + 3
\]

\[
(x \circ y) \circ z = (x \circ y)z + 3
= (xy + 3)z + 3
= xyz + 3z + 3
\]

olduğundan
$x \circ (y \circ z) \neq (x \circ y) \circ z$.
O hâlde $\circ$ işleminin birleşme özelliği yoktur.

Örnek:

$A = \{a, b, c, d\}$ kümesinde tanımlı $\star$ işleminin birleşme özelliğinin olup olmadığını inceleyelim.

\[
\begin{array}{c|cccc}
\star & a & b & c & d\\
\hline
a & b & c & d & a \\
b & c & d & a & b \\
c & d & a & b & c \\
d & a & b & c & d
\end{array}
\]

Örneğin $x = a$, $y = b$ ve $z = c$ seçelim.

\[
x \star (y \star z)
= a \star (b \star c)
= a \star a= b
\]

\[
(x \star y) \star z
= (a \star b) \star c
= c \star c= b
\]

Benzer şekilde $x, y, z$ yerine farklı elemanlar seçilip bu elemanlar için de \[x \star (y \star z) = (x \star y) \star z\] olduğu gösterilebilir. O hâlde birleşme özelliği vardır.

Uyarı:

$n$ elemanlı bir $A$ kümesi üzerinde tanımlanan bir $\star$ işleminin birleşme özelliğinin tam olarak anlaşılabilmesi için $n^3$ tane işlem yapılmalıdır.

Yukarıdaki örnekte $s(A) = 4$ olduğundan $4^3 = 64$ tane işleme ihtiyaç vardır.

4. Birim (Etkisiz) Eleman:

$A$ kümesi üzerinde bir $\star$ işlemi tanımlansın. $\forall x \in A$ için

\[
x \star e = e \star x = x
\]

olacak şekilde bir $e \in A$ varsa, $e$ elemanına $\star$ işleminin birim (etkisiz) elemanı denir.

$x \star e = x$ eşitliğinden elde edilen birim elemana sağdan birim eleman,

$e \star x = x$ eşitliğinden elde edilen birim elemana soldan birim eleman denir.

$\star$ işleminin sağdan birim elemanı ile soldan birim elemanı eşit ise bu işlemin birim elemanı vardır. Bir işlemde birim eleman varsa tek bir tane (sabit) dir.

Örnek:

$ \mathbb{Z} $ üzerinde tanımlanan
\[
x \circ y = x + y + 2xy
\]
işleminin birim elemanı varsa, bulalım.

\[
x \circ e = x
\quad \Rightarrow \quad
x + e + 2xe = x
\quad \Rightarrow \quad
(1 + 2x)e = 0
\quad \Rightarrow \quad
e = 0 \in \mathbb{Z}.
\]
O hâlde sağdan birim eleman $ e = 0 $dır.

\[
e \circ x = x
\quad \Rightarrow \quad
e + x + 2ex = x
\quad \Rightarrow \quad
(1 + 2x)e = 0
\quad \Rightarrow \quad
e = 0 \in \mathbb{Z}.
\]
O hâlde soldan birim eleman $ e = 0 $dır.

Buna göre $\mathbb{Z}$ de tanımlı $\circ$ işleminin birim elemanı $ e = 0 $dır.

Örnek:

$ \mathbb{N} $ üzerinde tanımlanan
\[
x \Delta y = x + y + 3
\]
işleminin birim elemanı varsa, bulalım.

\[
x \Delta e = x
\quad \Rightarrow \quad
x + e + 3 = x
\quad \Rightarrow \quad
e = -3 \notin \mathbb{N}
\]
olduğundan sağdan birim eleman yoktur.

\[
e \Delta x = x
\quad \Rightarrow \quad
e + x + 3 = x
\quad \Rightarrow \quad
e = -3 \notin \mathbb{N}
\]
olduğundan soldan birim eleman yoktur.

Buna göre $\mathbb{N}$ de tanımlı $\Delta$ işleminin birim elemanı yoktur.

Örnek:

\[
x \star e = x \;\;\Rightarrow\;\; 2x + x e = x
\]
\[
\Rightarrow x + x e = 0
\]
\[
\Rightarrow x (1 + e) = 0
\]

Burada, $1 + e = 0 \Rightarrow e = -1 \in \mathbb{R}^-$ olur. O hâlde sağdan birim eleman $e = -1$’dir.

\[
e \star x = x \;\;\Rightarrow\;\; 2e + e x = x
\]
\[
\Rightarrow (2 + x) e = x
\]

\[
\Rightarrow e = \frac{x}{2 + x}
\]

Burada $e$, sabit ($x$’ten bağımsız) olmadığından soldan birim eleman yoktur. Buna göre $\mathbb{R}^+$ de tanımlı $\star$ işleminin birim elemanı yoktur.

Örnek:

$\mathbb{Z}^-$ üzerinde tanımlanan
\[
x \circ y = x^2 – y^2
\]
işleminin birim elemanı varsa, bulalım.

\[
x \circ e = x \Rightarrow x^2 – e^2 = x
\]

\[
\Rightarrow e^2 = x^2 – x
\]

\[
\Rightarrow \sqrt{e^2} = \sqrt{x^2 – x}
\]

\[
\Rightarrow |e| = \sqrt{x^2 – x}
\]

Burada $e \in \mathbb{Z}^-$ olduğundan,

\[
\Rightarrow -e = \sqrt{x^2 – x} \Rightarrow e = -\sqrt{x^2 – x}
\]

Burada $e$, sabit ($x$’ten bağımsız) olmadığından sağdan birim eleman yoktur. O hâlde soldan birim elemana bakmaya gerek kalmaksızın $\mathbb{Z}^-$ de tanımlı olan $\circ$ işleminin birim elemanı yoktur.

Uyarı:

Değişme özelliği olan bir $\star$ işlemi verilsin.

\[
x \star e = e \star x = x
\]

olacağından, bu işlemin birim elemanını bulmak için sadece sağdan birim elemana veya sadece soldan birim elemana bakmak yeterlidir.

Örnek:

\[
x \star y = y \star x \;\;\Rightarrow\;\; \frac{xy}{2} = \frac{yx}{2}
\]

olduğundan $\star$ işleminin değişme özelliği vardır. O hâlde sadece sağdan birim elemana bakalım.

\[
x \star e = x \;\;\Rightarrow\;\; \frac{x e}{2} = x
\]

\[
\Rightarrow x e = 2x \;\;\Rightarrow\;\; x (e – 2) = 0
\]

\[
\Rightarrow e = 2
\]

Buna göre, $\mathbb{R}$ de tanımlı $\star$ işleminin birim elemanı $e = 2$’dir.

Örnek:

$\mathbb{R}$ üzerinde tanımlı

\[
x \circ y = x^3 + y^3
\]

işleminin birim elemanı varsa, bulalım.

\[
x \circ y = y \circ x \;\;\Rightarrow\;\; x^3 + y^3 = y^3 + x^3
\]

olduğundan $\circ$ işleminin değişme özelliği vardır. O hâlde sadece sağdan birim elemana bakalım:

\[
x \circ e = x \;\;\Rightarrow\;\; x^3 + e^3 = x
\]

\[
\Rightarrow e^3 = x – x^3
\]

\[
\Rightarrow e = \sqrt[3]{x – x^3}.
\]

Burada $e$, $x$’ten bağımsız (sabit) olmadığı için $\circ$ işleminin birim elemanı yoktur.

Uyarı:

İşlem tablosunda, başlangıç satırı ile aynı olan satırla, başlangıç sütunu ile aynı olan sütunun kesiştiği yerdeki eleman bu işlemin birim elemanıdır.
Eğer işlem tablosunun başlangıç satırı ile aynı olan satır veya başlangıç sütunu ile aynı olan sütun yoksa bu işlemin birim elemanı yoktur.

Örnek:

$A = \{a, b, c, d\}$ üzerinde tanımlanan $\star$ işleminin tablosu aşağıdaki gibidir. Bu işlemin birim elemanını bulalım:

\[
\begin{array}{c|cccc}
\star & a & b & c & d\\
\hline
a & b & c & d & a \\
b & c & d & a & b \\
c & d & a & b & c \\
d & a & b & c & d
\end{array}
\]

$\star$ işleminin birim elemanı $d$’dir.

Örnek:

$ A = \{ 0, 1, 2 \} $ üzerinde tanımlanan $\star$ işleminin tablosu aşağıdaki gibidir.

\[
\begin{array}{c|ccc}
\star & 0 & 1 & 2\\
\hline
0 & 1 & 1 & 1 \\
1 & 1 & 2 & 3 \\
2 & 1 & 3 & 5 \\
\end{array}
\]

İşlem tablosunda başlangıç satırı ile aynı olan satır ve başlangıç sütunu ile aynı olan sütun olmadığından bu işlemin birim elemanı yoktur.

Örnekler:

$\bullet \quad x + e = e + x = x \Rightarrow e = 0 $ olduğundan sayı kümeleri üzerinde toplama işleminin birim elemanı $ e = 0 $ dır.

$ \bullet \quad $ \[ x – e = x \Rightarrow e = 0 \] ve \[
e – x = x \Rightarrow e = 2x
\] olduğundan sayı kümeleri üzerinde çıkarma işleminin birim elemanı yoktur.

$ \bullet \quad x \cdot e = e \cdot x = x \Rightarrow e = 1 $ olduğundan sayı kümeleri üzerinde çarpma işleminin birim elemanı $ e = 1 $dir.

$\bullet$

\[
\frac{x}{e} = x \Rightarrow e = 1
\]

\[
\frac{e}{x} = x \Rightarrow e = x^2
\]

olduğundan sayı kümeleri üzerinde bölme işleminin birim elemanı yoktur.

$\bullet$ Her $ A $ kümesi için,

\[
A \cup Ø = Ø \cup A = A
\]

\[
A \cap E = E \cap A = A
\]

olduğundan kümeler üzerinde $\cup$ işleminin birim elemanı $ Ø $, $\cap$ işleminin birim elemanı $ E $ (evrensel küme)dir.

5. Bir Elemanın Tersi:

A kümesinde tanımlı bir $\star$ işleminin etkisiz elemanı $e$ olsun. Eğer $x \in A$ için,

\[
x \star x^{-1} = x^{-1} \star x = e
\]

olacak şekilde bir $ x^{-1} \in A $ varsa, $ x^{-1} $ elemanına $\star$ işlemine göre $ x $ elemanının tersi denir.

\[
x \star x^{-1} = e
\]

eşitliğinden elde edilen $ x^{-1} $ elemanına $ x $’in sağdan tersi,

\[
x^{-1} \star x = e
\]

eşitliğinden elde edilen $ x^{-1} $ elemanına $ x $’in soldan tersi denir.

$ x $’in sağdan tersi ile soldan tersi eşit ise $ x $’in $\star$ işlemine göre tersi vardır.

Örnek:

$ \mathbb{R} $ üzerinde tanımlı

\[
x \star y = x + y – 3xy
\]

işlemine göre, varsa, $ 2 $’nin tersini bulalım.

Önce $\star$ işleminin birim elemanını bulalım. $\star$ işleminin değişme özelliği olduğundan sadece sağdan birim elemana bakmak yeterlidir.

\[
x \star e = x \;\;\Rightarrow\;\; x + e – 3xe = x
\]

\[
\Rightarrow (1 – 3x) e = 0
\]

\[
\Rightarrow e = 0 \text{ dır.}
\]

$\star$ işleminin değişme özelliği olduğundan

\[
x \star x^{-1} = x^{-1} \star x = e
\]

olacağından sadece sağdan, $ x $’in tersini bulmak yeterlidir.

\[
x \star x^{-1} = e
\]

\[
2 \star 2^{-1} = 0
\]

\[
\Rightarrow 2 + 2^{-1} – 3 \cdot 2 \cdot 2^{-1} = 0
\]

\[
\Rightarrow -5 \cdot 2^{-1} = -2
\]

\[
\Rightarrow 2^{-1} = \frac{2}{5}
\]

olarak bulunur.

Örnek:

$ \mathbb{R} $ üzerinde tanımlı

\[
x \circ y = \frac{x + y – xy + 6}{7}
\]

işlemine göre, varsa, $ 3 $’ün tersini ve tersi olmayan elemanı bulalım.

Önce $\circ$ işleminin birim elemanını bulalım. $\circ$ işleminin değişme özelliği olduğundan sadece sağdan birim elemana bakmak yeterlidir.

\[
x \circ e = x \Rightarrow \frac{x + e – xe + 6}{7} = x
\]

\[
\Rightarrow x + e – xe + 6 = 7x
\]

\[
\Rightarrow (1 – x)(e + 6) = 0
\]

\[
\Rightarrow e + 6 = 0 \Rightarrow e = -6 \text{ dır.}
\]

Buradan, $ 1 – x = 0 \Rightarrow x = 1 $’in tersi yoktur. Çünkü,

\[
x \circ x^{-1} = e \Rightarrow 1 \circ 1^{-1} \overbrace{=}^{?} -6
\]

\[
\Rightarrow \frac{1 + 1^{-1} – 1 \cdot 1^{-1} + 6}{7} \overbrace{=}^{?} -6
\]

\[
\Rightarrow 7 \neq -42 \quad \text{dir.}
\]

Şimdi de $ 3 $’ün tersini bulalım.

$\circ$ işleminin değişme özelliği olduğundan sadece sağdan, $3$’ün tersini bulmak yeterlidir.

\[
x \circ x^{-1} = e \Rightarrow 3 \circ 3^{-1} = -6
\]

\[
\Rightarrow \frac{3 + 3^{-1} – 3 \cdot 3^{-1} + 6}{7} = -6
\]

\[
\Rightarrow 9 \;- \;2 \cdot 3^{-1}= -6.7
\]

\[
\Rightarrow 3^{-1} = \frac{51}{2}
\]

olarak bulunur.

Örnek:

$ \mathbb{R} $ üzerinde tanımlı

\[
x \Delta y = 2x + 2y + 2xy + 1
\]

işlemine göre, varsa, $ 1 $’in tersini ve tersi olmayan elemanı bulalım.

Önce $ \Delta $ işleminin birim elemanını bulalım.
$ \Delta $ işleminin değişme özelliği olduğundan sadece sağdan birim elemana bakmak yeterlidir.

\[
x \Delta e = x \Rightarrow 2x + 2e + 2xe + 1 = x
\]

\[
\Rightarrow (1 + x)(2e + 1) = 0
\]

\[
\Rightarrow 2e + 1 = 0 \Rightarrow e = -\frac{1}{2} \quad \text{dır.}
\]

Buradan $ 1 + x = 0 \Rightarrow x = -1 $ in tersi yoktur. Çünkü,

\[
x \Delta x^{-1} = e \Rightarrow 1 \Delta (-1)^{-1} \overbrace{=}^{?} – \frac{1}{2}
\]

\[
\Rightarrow 2 \cdot (-1) + 2 \cdot (-1)^{-1} + 2 \cdot (-1) \cdot (-1)^{-1} + 1 \overbrace{=}^{?} – \frac{1}{2}
\]

\[
\Rightarrow -1 \neq -\frac{1}{2} \quad \text{dir.}
\]

Şimdi de $ 1 $’in tersini bulalım. $ \Delta $ işleminin değişme özelliği olduğundan sadece sağdan, $1$’in tersini bulmak yeterlidir.

\[
x \Delta x^{-1} = e \Rightarrow 1 \Delta 1^{-1} = -\frac{1}{2}
\]

\[
\Rightarrow 2 \cdot 1 + 2 \cdot 1^{-1} + 2 \cdot 1 \cdot 1^{-1} + 1 = -\frac{1}{2}
\]

\[
\Rightarrow 4 \cdot 1^{-1} = -\frac{1}{2}\; -\; 2 \;-\; 1
\]

\[
\Rightarrow 1^{-1} = -\frac{7}{8} \quad \text{dir.}
\]

Örnek:

$ \mathbb{Z}^+ $ üzerinde tanımlı
\[
x \circ y = x + y – 2
\]
işlemine göre, varsa, $ 5 $’in tersini bulalım.

Önce $ \circ $ işleminin birim elemanını bulalım. $ \circ $ işleminin değişme özelliği olduğundan sadece sağdan birim elemana bakmakla, $ 5 $’in sadece sağdan tersini aramak yeterlidir.

\[
x \circ e = x \Rightarrow x + e – 2 = x
\]

\[
\Rightarrow e = 2 \quad \text{dir.}
\]

Şimdi de $ 5 $’in tersini bulalım.

\[
x \circ x^{-1} = e \Rightarrow 5 \circ 5^{-1} = 2
\]

\[
\Rightarrow 5 + 5^{-1} – 2 = 2
\]

\[
\Rightarrow 5^{-1} = -1 \notin \mathbb{Z}^+
\]

olduğundan $ 5 $’in tersi yoktur.

Örnek:

$ A = \{ 1, 2, 3, 4 \} $ üzerinde tanımlı $ \star $ işleminin tablosu aşağıdaki gibidir. $ 2 $’nin tersini bulalım.

\[
\begin{array}{c|cccc}
\star & 1 & 2 & 3 & 4\\
\hline
1 & 3 & 4 & 1 & 2 \\
2 & 4 & 1 & 2 & 3 \\
3 & 1 & 2 & 3 & 4 \\
4 & 2 & 3 & 4 & 1 \\
\end{array}
\]

$ \star $ işleminin birim elemanı $ 3 $’tür.

\[ x \star x^{-1} = e\]

\[\Rightarrow 2 \star 2^{-1} = 3 \]

\[ \Rightarrow 2^{-1} = 4 \]

olarak bulunur.

Örnek:

$ \mathbb{R}^2 $ üzerinde tanımlanan

\[
(x, y) \circ (a, b) = (xa, y + b + 1)
\]

işlemine göre $ (1,2) $’nin tersini bulalım.

$ \circ $ işleminin değişme özelliği olduğundan sadece sağdan birim elemana bakmak yeterlidir.

\[
(x, y) \circ (e_1, e_2) = (x, y)
\]

\[
\Rightarrow (xe_1, y + e_2 + 1) = (x, y)
\]

\[
\Rightarrow xe_1 = x \quad \text{ve} \quad y + e_2 + 1 = y
\]

\[
\Rightarrow e_1 = 1 \quad \text{ve} \quad e_2 = -1
\]

O hâlde birim eleman $ (e_1, e_2) = (1, -1) $ dir.

$ \circ $ işleminin değişme özelliği olduğundan sadece sağdan ters elemanı bulmak yeterlidir.

\[
(x, y) \circ (x^{-1}, y^{-1}) = (e_1, e_2)
\]

\[
\Rightarrow (1,2) \circ (1^{-1}, 2^{-1}) = (1, -1)
\]

\[
\Rightarrow (1 \cdot 1^{-1} , 2 + 2^{-1} + 1) = (1 , -1)
\]

\[
\Rightarrow 1 \cdot 1^{-1} = 1 \quad \text{ve} \quad 2 + 2^{-1} + 1 = -1
\]

\[
\Rightarrow 1^{-1} = 1 \quad \text{ve} \quad 2^{-1} = -4 \quad \text{olur.}
\]

O hâlde $ (1,2) $ nin $ \circ $ işlemine göre tersi $ (1, -4) $ tür.

6. Dağılma Özelliği:

A kümesi üzerinde $ \circ $ ve $ \star $ işlemleri tanımlansın. $\forall x, y, z \in A$ için,

\[
x \star (y \circ z) = (x \star y) \circ (x \star z)
\]

oluyorsa, $ \star $ işleminin $ \circ $ işlemi üzerine $ \textbf{soldan dağılma} $ özelliği vardır.

\[
(x \circ y) \star z = (x \star z) \circ (y \star z)
\]

oluyorsa, $ \star $ işleminin $ \circ $ işlemi üzerine $ \textbf{sağdan dağılma} $ özelliği vardır.

$ \star $ işleminin $ \circ $ işlemi üzerine hem soldan hem de sağdan dağılma özelliği varsa, $ \star $ işleminin $ \circ $ işlemi üzerine $ \textbf{dağılma özelliği} $ vardır.

Örnek:

$ \mathbb{R} $ üzerinde tanımlı
\[
x \star y = 2x + y
\]
ve
\[
x \circ y = x + y + 3
\]
işlemleri veriliyor.

$ \star $ işleminin $ \circ $ işlemi üzerine dağılma özelliğinin olup olmadığını inceleyelim.

$\forall x, y, z \in \mathbb{R}$ için,

\[
x \star (y \circ z) = x \star (y + z + 3)
\]

\[
= 2x + y + z + 3
\]

\[
(x \star y) \circ (x \star z) = (2x + y) \circ (2x + z)
\]

\[
= (2x + y) + (2x + z) + 3
\]

\[
= 4x + y + z + 3
\]

olur.

O hâlde,

\[
x \star (y \circ z) \neq (x \star y) \circ (x \star z)
\]

olduğundan $ \star $ işleminin $ \circ $ işlemi üzerine soldan dağılma özelliği olmadığı için, $ \star $ işleminin $ \circ $ işlemi üzerine dağılma özelliği yoktur.

Örnek:

$ \mathbb{R} $ üzerinde tanımlı
\[
x \star y = x + y + 1
\]
ve
\[
x \circ y = 2x – y
\]
işlemleri veriliyor.

$ \star $ işleminin $ \circ $ işlemi üzerine dağılma özelliğinin olup olmadığını inceleyelim.

$\forall x, y, z \in \mathbb{R}$ için,

\[
x \star (y \circ z) = x \star (2y – z)
\]

\[
= x + 2y – z + 1
\]

\[
(x \star y) \circ (x \star z) = (x + y + 1) \circ (x + z + 1)
\]

\[
= 2(x + y + 1) – (x + z + 1)
\]

\[
= x + 2y – z + 1
\]

olur. O hâlde,

\[
x \star (y \circ z) = (x \star y) \circ (x \star z)
\]

olduğundan $ \star $ işleminin $ \circ $ işlemi üzerine soldan dağılma özelliği vardır.

\[
(x \circ y) \star z = (2x – y) \star z
\]

\[
= 2x – y + z + 1
\]

\[
(x \star z) \circ (y \star z) = (x + z + 1) \circ (y + z + 1)
\]

\[
= 2(x + z + 1) – (y + z + 1)
\]

\[
= 2x + z – y + 1
\]

olur. O hâlde,

\[
(x \circ y) \star z = (x \star z) \circ (y \star z)
\]

olduğundan $ \star $ işleminin $ \circ $ işlemi üzerine sağdan dağılma özelliği vardır.

O hâlde, $ \star $ işleminin $ \circ $ işlemi üzerine dağılma özelliği vardır.

Örnek:

$ A = \{ 0, 1, 2, 3 \} $ kümesi üzerinde tanımlanan $ \star $ ve $ \circ $ işlemlerinin tabloları verilmiştir. $ \star $ işleminin $ \circ $ işlemi üzerine dağılma özelliğini inceleyelim.

\[
\begin{array}{c|cccc}
\star & 0 & 1 & 2 & 3\\
\hline
0 & 0 & 1 & 2 & 3 \\
1 & 1 & 2 & 3 & 0 \\
2 & 2 & 3 & 0 & 1 \\
3 & 3 & 0 & 1 & 2 \\
\end{array}
\quad \quad \quad
\begin{array}{c|cccc}
\circ & 0 & 1 & 2 & 3\\
\hline
0 & 1 & 2 & 3 & 0 \\
1 & 2 & 3 & 0 & 1 \\
2 & 3 & 0 & 1 & 2 \\
3 & 0 & 1 & 2 & 3 \\
\end{array}
\]

$\forall x, y, z \in A$ için, $ \Rightarrow x = 1, y = 2, z = 3 $ seçelim.

\[
x \star (y \circ z) = 1 \star (2 \circ 3)
\]

\[
= 1 \star 2 = 3
\]

\[
(x \star y) \circ (x \star z) = (1 \star 2) \circ (1 \star 3)
\]

\[
= 3 \circ 0 = 0
\]

olduğundan soldan dağılma özelliği yoktur. O hâlde $\star $ işleminin $\circ $ işlemi üzerine dağılma özelliği yoktur.

7. Yutan Elaman:

A kümesi üzerinde bir $ \star $ işlemi tanımlansın. Eğer $\forall x \in A$ için,

\[
x \star y = y \star x = y
\]

olacak şekilde bir $ y \in A $ varsa, $ y $ ye $ \star $ işleminin yutan elemanı denir.

\[
x \star y = y
\]

eşitliğinden elde edilen $ y $ ye sağdan yutan eleman,

\[
y \star x = y
\]

eşitliğinden elde edilen $ y $ ye soldan yutan eleman denir.

Sağdan yutan eleman soldan yutan elemana eşit ise $ \star $ işleminin yutan elemanı vardır.

Bir işlemde yutan eleman varsa tek bir tane sabit dir. İşlemin değişme özelliği varsa sadece sağdan yutan elemana veya sadece soldan yutan elemana bakmak yeterlidir.

Örnek:

$ \mathbb{R} $ üzerinde tanımlı
\[
x \star y = \frac{xy}{2} + x + y
\]
işleminin yutan elemanının olup olmadığını inceleyelim.

$ \star $ işleminin değişme özelliği olduğundan sadece sağdan yutan elemana bakmak yeterlidir.

\[
x \star y = y \Rightarrow \frac{xy}{2} + x + y = y
\]

\[
\Rightarrow x \left( \frac{y}{2} + 1 \right) = 0
\]

\[
\Rightarrow \frac{y}{2} + 1 = 0 \Rightarrow y = -2
\]

olarak bulunur.

Örnek:

$ \mathbb{Z}^- $ üzerinde tanımlı
\[
x \circ y = \frac{xy}{x + y+1}
\]
işleminin yutan elemanının olup olmadığını inceleyelim.

$ \circ $ işleminin değişme özelliği olduğundan sadece sağdan yutan elemana bakmak yeterlidir.

\[
x \circ y = y \Rightarrow \frac{xy}{x + y + 1} = y
\]

\[
\Rightarrow xy = xy + y^2 + y
\]

\[
\Rightarrow 0 = y^2 + y
\]

\[
\Rightarrow y = 0 \quad \text{veya} \quad y = -1
\]

Burada $ y \in \mathbb{Z}^- $ olduğundan $ \circ $ işleminin yutan elemanı $ y = -1 $ olarak bulunur.

Uyarı:

Bir işlemin yutan elemanı varsa, bu işleme göre yutan elemanın tersi yoktur.

Örnek:

$\forall x \in \mathbb{R}$ için,

\[
x \cdot 0 = 0 \cdot x = 0
\]

olduğundan çarpma işleminin yutan elemanı $ 0 $ (sıfır) dır. $ 0 $ (sıfır) ın çarpma işlemine göre tersinin olmadığını gösterelim.

\[
x \cdot x^{-1} = e \Rightarrow 0 \cdot 0^{-1} = 1
\]

\[
\Rightarrow 0^{-1} = \frac{1}{0} \notin \mathbb{R}
\]

dır. O hâlde $ 0 $ (sıfır) ın çarpmaya göre tersi yoktur.

Örnek:

$ \mathbb{R} $ üzerinde tanımlanan

\[
x \star y = xy + 1
\]

işleminin yutan elemanının olup olmadığını inceleyelim.

$ \star $ işleminin değişme özelliği olduğundan sadece sağdan yutan elemana bakmak yeterlidir.

\[
x \star y = y \Rightarrow xy + 1 = y
\]

\[
\Rightarrow y = \frac{1}{1 – x}
\]

sabit olmadığından $ \star $ işleminin yutan elemanı yoktur.

Uyarı:

$ A $ kümesi üzerinde tanımlanan $ \star $ işleminin tablosu verilsin. Tabloda, bir satır (başlangıç sütunundan itibaren) ile bir sütun (başlangıç satırından itibaren) aynı elemandan meydana gelmiş ise bu eleman $ \star $ işleminin yutan elemanıdır.

Örnek:

\[
\begin{array}{c|ccc}
\star & a & b & c\\
\hline
a & b & a & c \\
b & a & a & a \\
c & b & a & c \\
\end{array}
\]

Yutan eleman yoktur.

\[
\begin{array}{c|cccc}
\star & a & b & c & d\\
\hline
a & a & a & a & a \\
b & a & b & b & b \\
c & a & b & c & c \\
d & a & b & c & d \\
\end{array}
\]

$ a $ yutan elemandır.