Kümeler Üzerinde Yapılan İşlemler
1. Kümelerin Kesişimi
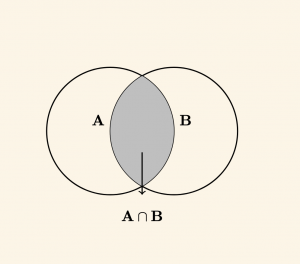
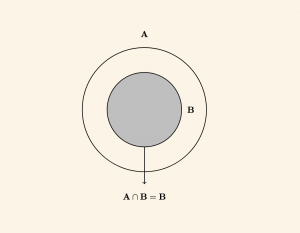
A ile B kümelerindeki ortak elemanların meydana getirdiği kümeye A kesişim B kümesi denir. \( A \cap B \) şeklinde gösterilir.
\[ A \cap B = \{ x \;| \; x \in A \;\; \text{ve } \; x \in B \} \;\; \text{dir. } \]
Örnek:
\[
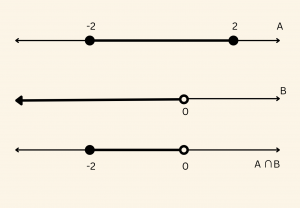
A = \{x : |x| \leq 2, \, x \in \mathbb{R} \} \quad \text{ve} \quad
B = \{x : x < 0, \, x \in \mathbb{R} \} \, \text{ise,}
\]
\[
A \cap B \, \text{kümesini bulalım.}
\]
\[
|x| \leq 2 \implies -2 \leq x \leq 2 \quad \text{ve} \quad A = [-2, 2]
\]
\[
B = (-\infty, 0) \, \text{olduğundan,}
\]
\[
A \cap B = [-2, 0) \;\; \text{dır. }
\]
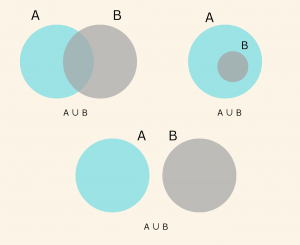
2. Kümelerin Birleşimi
A ile B kümelerindeki tüm elemanların meydana getirdiği kümeye A birleşim B kümesi denir. \( A \cup B \) şeklinde gösterilir.
\[ A \cup B = \{ x\; | \; x \in A \;\; \text{veya } x \in B \} \] dir.
3.Kesişim ve Birleşimin Özellikleri:
\( 1) \quad \) Kesişim ve birleşim işleminin değişme özelliği vardır.
\[ \begin{array}{c} A \cap B = B \cap A \\ A \cup B = B \cup A \end{array} \]
\( 2) \quad \) Kesişim ve birleşim işleminin birleşme özelliği vardır.
\[ \begin{array}{c}
A \cap B \cap C = ( A \cap B) \cap C = A \cap (B \cap C ) \\
A \cup B \cup C = ( A \cup B) \cup C = A \cup (B \cup C )
\end{array}
\]
\( 3) \quad \) Kesişimin birleşim üzerine ve birleşimin kesişim üzerine dağılma özelliği vardır.
\[ \begin{array}{c}
A \cap (B \cup C ) = ( A \cap B) \cup (A \cap C) \\
A \cup (B \cap C ) = ( A \cup B) \cap (A \cup C)
\end{array}
\]
\( 4) \quad \) De Morgan Kuralları
\[ \begin{array}{c}
(A \cap B )’ = A’ \cup B’ \\
(A \cup B )’ = A’ \cap B’ \\
\end{array}
\]
\( 5) \quad \)
\[
\begin{array}{c}
A \cap A’= Ø, \quad A \cap Ø = Ø , \quad A \cap E = A \\
A \cup A’ = E, \quad A \cup Ø = A,, \quad A \cup E = E\\
\end{array}
\]
Soru 4
\([A \cap( A \cap B’) ] \cup (A’ \cap B) \) işleminin sonucu aşağıdakilerden hangisidir?
\[
\text{A)} A \cup B \quad
\text{B) } A \quad
\text{C) } B\quad
\text{D) } A’ \quad
\text{E) } B’
\]
Çözüm:
\[ A \cap (A \cap B’)’ \cup (A’ \cup B ) \]
De Morgan Kuralı uygulanırsa,
\[ = [A \cap (A’ \cup B )] \cup (A’ \cap B) \]
Dağılma özelliği uygulanırsa
\[ = [ (A \cap A’ ) \cup (A \cap B ) ] \cup (A’ \cap B ) \]
\[ = [Ø \cup (A \cap B ) \cup (A’ \cap B) ]\]
\[ (A \cap B ) \cup (A’ \cap B)\]
Dağılma özelliğinden,
\[ B \cap (A \cup A’ ) = B \cap E = B \]
\(\textbf{Cevab: C} \)
Soru 5
Yandaki şekle göre \( s[(( B \cap C) \cup A’) ]\) kaçtır?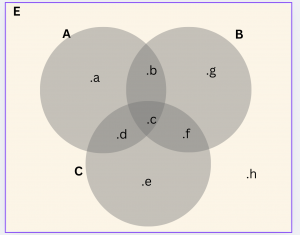
\[
\text{A)} 3 \quad
\text{B) } 4 \quad
\text{C) } 5\quad
\text{D) } 6 \quad
\text{E) } 7
\]
Çözüm:
\[ B \cap C = \{ c, f \} \;\; \text{ve } \;\; A= \{ a,b,c,d \} \]
\[ (B \cap C) \cup A = \{ a, b, c ,d , f \} \]
\[ ( (B \cap C) \cup A’) = \{ e, g, h \} \;\; \text{olduğuna göre } \]
\[ s[(( B \cap C) \cup A’) = 3 \; \text{tür. } \]
\(\textbf{Cevab: A} \)
4. Birleşim Kümesinin Elaman Sayısı:
\[ s(A \cup B ) = s(A) + s(B)- s(A \cap B) \]
\[ s(A \cup B \cup C ) = s(A) + s(B) + s(C) – \left[ s(A \cap B) + s( A \cap C) + s( B \cap C) \right] + s(A \cap B \cap C) \]
Soru 6
\( s(A) = 2x- 3, \;\; s(B) = 3x+ 4, \;\; s(A \cup B) = 3x+7 \;\; \text{ve } \; A \cap B \neq Ø \) ise x in en küçük değeri kaçtır?
\[
\text{A)} 3 \quad
\text{B) } 4 \quad
\text{C) } 5\quad
\text{D) } 6 \quad
\text{E) } 7
\]
Çözüm:
\[ s(A \cup B ) = s(A) + s(B) – s( A \cap B) \]
\[ 3x+ 7 = 2x-3 + 3x + 4 – s( A \cap B) \]
\[\Rightarrow s( A \cap B) = 2x-6 \]
\[ A \cap B \neq Ø \quad \text{ise } \quad s( A \cap B)> 0 \]
O halde, en küçük \(x \) değeri 4 tür.
\(\textbf{Cevab: B} \)
Soru 7
45 kişilik bir sınıftaki öğrencilerden Ankara’yı görenler 23, İstanbul’u görenler 18, Bursa’yı görenler de 14 kişidir. 5 kişi hem Ankara’yı hem İstanbul’u, 10 kişi hem Ankara’yı hem Bursa’yı, 7 kişi de hem İstanbul’u hem de Bursa’yı görmüştür. 9 kişi bu üç şehirden hiçbirini görmediğine göre, her üç sehri de gören kaç kişidir?
\[
\text{A)} 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
9 kişi, bu üç şehirden hiçbirisini görmediğine göre, \(45-9 =36 \) kişi Ankara’yı veya İstanbul’u veya Bursa’yı görmüştür. Buna göre,
\[ s( A \cup B \cup I ) = s(A) + s(B) + s(İ) – [ s(A \cap İ ) + s( A \cap B) + s(İ \cap B) ] + s(A \cap B \cap İ) \]
\[ 36 = 23 + 18 + 14 \:-\; [5+ 10 + 7 ] + s(A \cap B \cap İ) \]
\[ \Rightarrow s(A \cap B \cap İ) = 3 \]
3 kişi, Ankara, istanbul ve Bursa şehirlerinin üçünü de görmüştür.
\(\textbf{Cevab: C} \)
Soru 8
\[ A = \{x \; | \; x < 200, x = 7k , k \in Z^+ \}\]
\[ B = \{x \; | \; x < 351, x = 3k , k \in Z^+ \}\]
kümeleri veriliyor, \( s(A \cup B) \) kaçtır?
\[
\text{A)} 133 \quad
\text{B) } 134 \quad
\text{C) } 135 \quad
\text{D) } 136 \quad
\text{E) } 137
\]
Çözüm:
A, 7 ile bölünebilen 200 den küçük pozitif tamsayıların kümesi olduğuna göre,
\[ 199 \div 7 = 28 \quad \text{Kalan: } 3 \Rightarrow s(A) = 28 \]
B, 3 ile tam bölünebilen 351 den küçük pozitif tamsayıların kümesi olduğuna göre,
\[ 351 \div 3 = 116 \quad \text{Kalan: } 2 \Rightarrow s(B) = 116 \]
\( A \cap B \) , 21 (hem 7 hem de 3) ile bölünebilen 200 den küçük pozitif tamsayıların kümesidir. O halde,
\[ 199 \div 21 = 9 \quad \text{Kalan: } 10 \Rightarrow s(A \cap B) = 9 \]
olduğuna göre,
\[s(A \cup B) = s(A) + s(B) – s(A \cap B) \]
\[ \quad \quad = 28 + 116 \; -\; 9 = 135\]
\(\textbf{Cevab: C} \)
Uyarı:
Aşağıdaki şekiller :
\( 1) \quad \) \( s(A \cap B = 0) \)

\[ s(A \cup B ) \text{ nin en büyük olduğu durumu, } \]
\( 2) \quad \) \( s(A \cap B \neq Ø ) \quad \quad ( ( A \cap B ) =1 ) \)
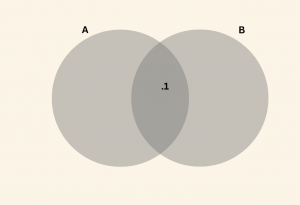
\[ s(A \cup B ) \text{ nin en büyük olduğu durumu, } \]
\( 3) \quad \) \( B \subset A \) \( (s(A \cap B) = s(B) )\)
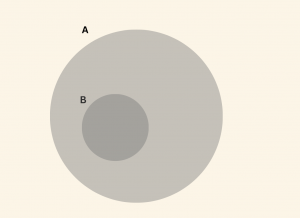
\( s(A \cap B ) \) nin en büyük \( s(A \cup B ) \) nin en küçük değeri aldığı durumu göstermektedir.
Soru 9
\( s(A)= 8, \;\; s(B)=6, \;\; \) ve \( s (A \cap B) \neq Ø \) ise \( s(A \cap B)\) nin alabileceği en büyük değer ile \( s(A \cup B) \) nin alabileceği en büyük değerin toplamı kaçtır?
\[
\text{A)} 16 \quad
\text{B) } 17 \quad
\text{C) } 18 \quad
\text{D) } 19 \quad
\text{E) } 20
\]
Çözüm:
\[ s(A \cap B ) \quad \text{nin en büyük değeri } 6\]
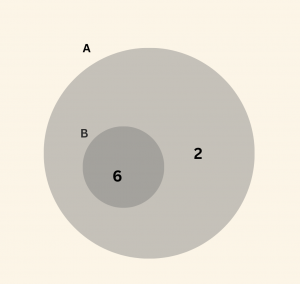
\[ s(A \cup B ) \quad \text{nin en büyük değeri } 13 \]
Bu iki değerin toplamı \( 6 + 13 = 19\) olur.
\(\textbf{Cevab: D} \)
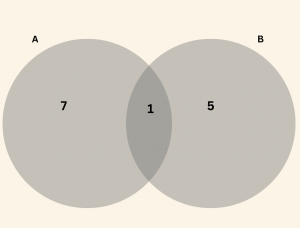
5. İki Kümenin Farkı
A ve B iki küme olsun. A da olup da B de olmayan elemanların meydana getirdiği kümeye A fark B kümesi denir.
\[ A – B = A \setminus B = \{ x \mid x \in A \;\; \text{ ve }\; x \notin B \} \]
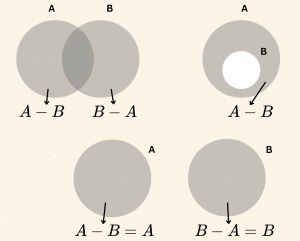
Özellikler:
\(1) \quad A-B = A \;- \; (A \cap B ) = A \cap B’ \)
\(2) \quad E \;-\; A = A’ \)
\(3) \quad (A\; -\; B) \cup (B \;- \; A ) = A \; \triangle \; B \; \) (Simetrik Fark)
Soru 10
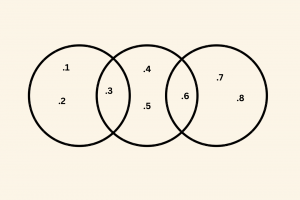
Yukarıdaki şekle göre \(s ((B \setminus A) \cap (B \setminus C) \) kaçtır?
\[
\text{A)} 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[ B \setminus A = \{ 4, 5, 6 \} \]
\[ B \setminus C = \{3, 4, 5 \} \]
\[ (B \setminus A ) \cap (B \setminus C ) = \{ 4, 5 \} \]
\[ \Rightarrow s((B \setminus A) \cap (B \setminus C) =2 \]
\(\textbf{Cevab: B} \)
Soru 11
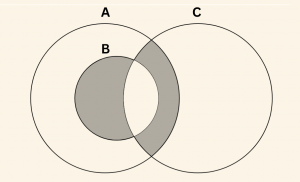
Şekildeki taralı bölgeyi aşağıdakilerden hangisi ifade eder?
\[
\text{A)}( A \; – \;B ) \cup C \quad
\text{B) } ( A\; – \;B ) \cap C \quad
\text{C) } ( A \cap C ) \cup B \quad
\text{D) } (C\; – \;B ) \cap A \quad
\text{E) } (B \;- \;C) \cup ((A \cap C )\; -\; B)
\]
Çözüm:
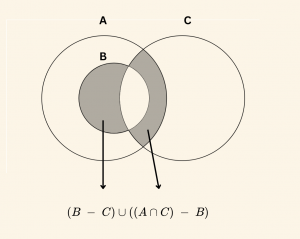
\(\textbf{Cevab: E} \)
Soru 12
\( [(A \cap B ) \cap (A \cup A’ )] \cup ( A \; -\; B) \) ifadesinin eşiti aşağıdakilerden hangisidir?
\[
\text{A)} A \quad
\text{B) } B \quad
\text{C) } A \cap B \quad
\text{D) }A’ \quad
\text{E) } B’
\]
Çözüm:
\[ [(A \cap B ) \cap (A \cup A’ )] \cup ( A \; -\; B) \]
\[ = [(A \cap B ) \cap E ] \cup ( A \cap B’) \]
\[ = [(A \cap B ) \cup (A \cap B’) ]= A \cap (B \cup B’) \]
\[ = A \cap E = A \]
\(\textbf{Cevab: A} \)
Uyarı:
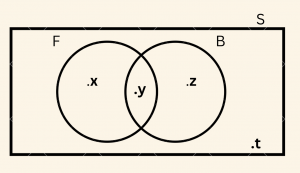
\(x + y + z + t \) tane öğrencinin bulunduğu bir sınıfta;
\( \bullet \quad \) Futbol oynayanların kümesi: F,
\( \bullet \quad \) Basketbol oynayanların kümesi: B,
\(x, y, z \) ve \(t \) içinde bulundukları kümelerin eleman sayılarını göstermek üzere,
x: sadece futbol oynayanların, sayısı,
y: futbol ve basketbol oynayanların sayısı,
z : sadece basketbol oynayanların sayısı,
t: hiçbir oyun oynamayanların sayısı,
\( x + y+ z \) : en az bir oyun oynayanların sayısı,
\( x + z + t \) : en çok bir oyun oynayanların sayısıdır.
Soru 13
\( s(A \cap B ) = s(A-B) = s(B-A), \,\; s(A’) = 5 \) ve \(s(A’ \cap B’) = 3 \) ise \( s(A \cup B)\) kaçtır?
\[
\text{A)} 15 \quad
\text{B) } 12 \quad
\text{C) } 9 \quad
\text{D) } 6 \quad
\text{E) } 3
\]
Çözüm:
 \[s(A \cap B) = s(A-B) = s(B-A) = x \quad \text{olsun } \]
\[s(A \cap B) = s(A-B) = s(B-A) = x \quad \text{olsun } \]
\[s(A’ \cap B’) = s[(A \cup B)’] = 3 \]
\[s(A’)= 5= x+3 \Rightarrow x= 2 \]
\[ s(A \cup B) = 3x = 6 \]
\(\textbf{Cevab: D} \)
Soru 14
E Evrensel Küme olmak üzere
\[ [s(A \cup B ) – s(A \cap B) ] = s(A’ \cap B’) = 8 \quad \text{ve } \; s(A \cap B )= 3 \] ise \( s(E) \) kaçtır?
\[
\text{A)} 17 \quad
\text{B) } 18 \quad
\text{C) } 19 \quad
\text{D) } 20 \quad
\text{E) } 21
\]
Çözüm:
\[ s(A’ \cap B’) = s[(A \cup B)’] = 8 \]
\[ s[(A \cup B) – s(A \cap B) = 8 ] = x +y \]
\[ s(E) = x + y + 3 +8 = 8+ 11 = 19\]
\(\textbf{Cevab: C} \)
Soru 15
\[ s(A \; -\; B) = x^2, \quad s(A \cap B) = 16, \quad s(A)= 8x \;\; \text{ve } \; s(A’ \cap B= 4 )\]
ise \(s(A \cup B ) \) kaçtır?
\[
\text{A)} 36 \quad
\text{B) } 35 \quad
\text{C) } 34 \quad
\text{D) } 33 \quad
\text{E) } 32
\]
Çözüm:
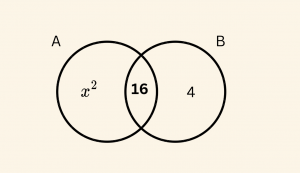
\[ s(A’ \cap B) = s( B-A)= 4 \]
\[s(A)= s(A-B) + s(A \cap B) \]
\[8x= x^2+16 \]
\[ \Rightarrow x^2 – 8x+16=0 \]
\[ (x-4)^2=0 \Rightarrow x= 4 \]
\[ s(A \cup B) = x^2 +16+4= 36\]
\(\textbf{Cevab: A} \)
Soru 16
E evrensel küme olmak üzere
\[ A \cup B \cup C =E, \quad B \subset A, \quad B \cap C = Ø, \]
\[ \text{ve} \]
\[ s(C-A)= 10, \quad s(A)= 16 \;\; \quad \text{ve } \;\; s(B’)=23 \]
ise \( s(B) \) kaçtır?
\[
\text{A)} 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
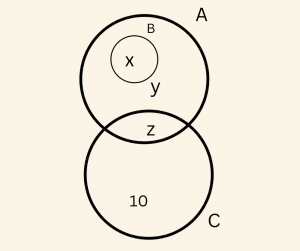
\[ s(B’)= 23 = y +z+10 \Rightarrow y+z = 13 \]
\[\Rightarrow s(A)= 16 = x+y+z \]
\[\Rightarrow 16= x+13 \]
\[ x = s(B) = 3\]
\(\textbf{Cevab: C} \)
Soru 17
\[ ( A \cap C ) \cup (B \cap C ) = Ø, \quad s[(A \cup B’)] =9 \]
\[ \text{ve} \]
\[ s[(A \cup B \cup C)’ ] = 4 \] ise s(C) kaçtır?
\[
\text{A)} 2 \quad
\text{B) } 3 \quad
\text{C) } 4 \quad
\text{D) } 5 \quad
\text{E) } 6
\]
Çözüm:
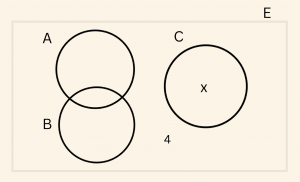
\[ ( A \cap C ) \cup (B \cap C ) = Ø \Rightarrow C \cap ( A \cup B) = Ø \]
\[ s[(A \cup B )’ ] = 9 = x+ 4 \]
\[\quad \quad \Rightarrow x = 5 \quad \text{olduğundan} \]
\[ s(C) = 5 \]
\(\textbf{Cevab: D} \)
Soru 18
Bir sınıfta, basketbol veya voleybol oyunlarından yalnız birini oynayan toplam 14, en az birini oynayan 21, en çok birini oynayan 27 öğrenci vardır. Buna göre, bu sınıfın mevcudu kaçtır?
\[
\text{A)} 30 \quad
\text{B) } 31 \quad
\text{C) } 32 \quad
\text{D) } 33 \quad
\text{E) } 34
\]
Çözüm:
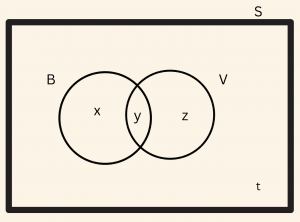
Sınıfta, basketbol oynayanların kümesi \( B \), voleybol oynayanların kümesi \( V \) olsun. Şemaya göre, yalnız bir oyunu oynayanların sayıları toplamı: \[ x + z = 14 \] En az bir oyunu oynayanların sayısı: \[ x + y + z = 21 \] En çok bir oyunu oynayanların sayısı: \[ x + z + t = 27 \] Buradan, \( t \)’yi bulalım: \[ 14 + t = 27 \Rightarrow t = 13 \] Buna göre, sınıf mevcudu: \[ x + y + z + t = 21 + 13 = 34 \]
\(\textbf{Cevab: E} \)
Soru 19
45 kişilik bir sınıfta, İngilizce dersinden başarılı olan 15 kişi vardır. 13 kişi matematikten, 6 kişi de her iki dersten başarısızdır. Buna göre, bu sınıfta sadece bir dersten başarılı olan kaç kişi vardır?
\[
\text{A)} 30 \quad
\text{B) } 31 \quad
\text{C) } 32 \quad
\text{D) } 33 \quad
\text{E) } 34
\]
Çözüm:
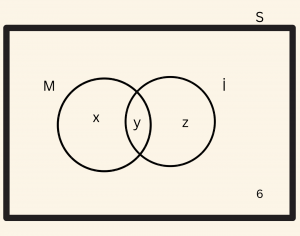
Sınıf mevcudu: \[ x + y + z + 6 = 45 \] \[ x + y + z = 39 \]
İngilizce’den başarılı olanların sayısı:
\[ y + z = 15 \] \[ x + 15 = 39 \Rightarrow x = 24 \]
Matematikten başarılı olanların sayısı:
\[ x + y = 13 \]
Matematikten başarısız olanların sayısı:
\[ z + 6 = 13 \quad \text{ise } z = 7 \quad \]
olduğuna göre, sadece bir dersten başarılı olanların sayısı
\[x + z =24 + 7 = 31 \]
\(\textbf{Cevab: B} \)
Soru 20
En az bir yabancı dil bilenlerin bulunduğu bir grupta, Fransızca bilenlerin tamamı İngilizce bilmektedir. Sadece Almanca bilenlerin sayısı 3, sadece İngilizce bilenlerin sayısı 5, Almanca bilenlerin sayısı 6 ve en az iki dil bilenlerin sayısı 7 ise Almanca bilmeyen kaç kişi vardır?
\[
\text{A)} 6 \quad
\text{B) } 7 \quad
\text{C) } 8 \quad
\text{D) } 9 \quad
\text{E) } 10
\]
Çözüm:
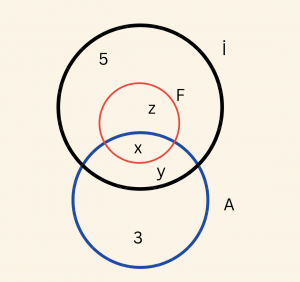
Fransızca bilenlerin kümesini F, İngilize bilenlerin kümesini İ, Almanca bilenlerin kümesini A ile gösterelim. Yabancı dil bilmeyen olmadığına göre, \( A \cup F \cup İ \) kümesi evrensel küme E, Fransızca bilenlerin tamamı ingilize bildiğine göre, \( F \subset İ \) dir.
Almanca bilenlerin sayısı: \[ x + y + 3 = 6 \] \[ \Rightarrow x + y = 3 \] En az iki dil bilenlerin sayısı: \[ x + y + z = 7 \] \[ \Rightarrow 3 + z = 7 \] \[ \Rightarrow z = 4 \] Almanca bilmeyenlerin sayısı: \[ z + 5 = 4 + 5 = 9 \]
\(\textbf{Cevab: D} \)
Soru 21
Futbol, voleybol veya basketbol oyunlarından en az birini oynayanların bulunduğu bir sınıfta, futbol oynayanlar basketbol oynayamamaktadır. Sadece futbol oynayanlar 4, sadece voleybol oynayanlar 5, futbol ve voleyboldan her ikisini de oynayanlar 3, futbol veya basketbol oynayanlar 14 ve voleybol oynayanlar 11 kişi ise sadece basketbol oynayanlar kaç kişidir?
\[
\text{A)} 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
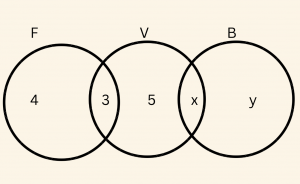
Futbol oynayanların kümesini \( F \), voleybol oynayanların kümesini \( V \), basketbol oynayanların kümesini \( B \) ile gösterelim. Bu sınıf üç oyundan en az birini oynayanlardan meydana geldiğine göre, \[ F \cup B \cup V \] evrensel küme olur. Futbol oynayanlar basketbol oynamadığına göre, \[ F \cap B = Ø \] olur.
Futbol veya basketbol oynayanların sayısı:
\[ 4+ 3 +x +y = 14 \Rightarrow x+ y = 7 \]
Voleybol oynayanların sayısı:
\[ 3 + 5 +x = 11 \Rightarrow x = 3\]
Sadece basketbol oynayanların sayısı:
\[ y= 7-x \Rightarrow 7-3 = 4 \quad \text{olur. } \]
\(\textbf{Cevab: D} \)
← Önceki Sayfa | Sonraki Sayfa →