Kümelerin Gösterilişi
1. Ortak Özellik Yöntemi:
Kümenin elemanlarının ortak özellikleri belirtilerek, küme ifade edilir.
Örnekler:
\(\bullet \quad \) A kümesi, mutlak değerce 3 ten küçük tam sayıların kümesi ise,
\[ A= \{x: \; |x| \; < \; 3 , x \in Z \} \] veya
\[ A= \{x| \; |x| \; < \; 3 , x \in Z \} \]
şeklindedir:
- İki Nokta Üst Üste (:) veya (|) burada “öyle ki” anlamında kullanılmıştır.
- Bu, kümenin elemanlarının sahip olduğu özellikleri tanımlamak için bir ayraç görevi görür.
Anlamı:
Bu ifade şunu anlatır:
- A kümesi, öyle ki x elemanıdır ve iki şartı sağlar:
- |x| < 3 (Mutlak değeri 3’ten küçük).
- x ∈ Z (x bir tam sayıdır).
Kümenin Elemanları:
- |x| < 3 demek, -3 < x < 3 aralığında olmalıdır.
- Ancak, x yalnızca tam sayılar kümesinden alınabilir.
Bu durumda:
- A = { -2, -1, 0, 1, 2 }
Burada iki nokta üst üste kullanılmış olması (veya | )yazım tarzından ibarettir ve herhangi bir anlam farkı oluşturmaz.
\(\bullet \quad \) B kümesi, ardışık çift sayıların kümesi ise,
\[ B= \{x| \; x = 2n , n \in Z \} \; \text{dir. } \]
2. Liste Yöntemi:
Kümenin elemanları, \( \{\}\) sembolünün içine birbirinden virgülle ayrılarak yazılır.
Örnek:
A kümesi, bir basamaklı asal sayıların kümesi ise \(A = \{ 2, 3, 5, 7 \} \) dir.
3. Venn Şeması Yöntemi:
Kümenin elemanları, kapalı bir eğri içinde, elemanların yanına nokta konarak yazılır.
Örnek:
A kümesi, alfabemizin sesli harflerinin kümesi ise,
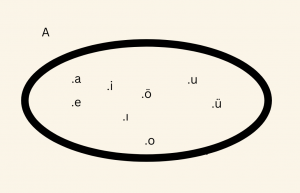
şeklinde gösterilir.
Aralik Kavrami:
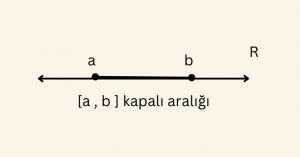
\[ A = \{ x | \; \; a ≤ x ≤ b , \;\;\ a,b, x \in R \} \] kümesi,
\[ A= [a, \; b ] \] şeklinde gösterilir.
\[ A = \{ x | \; \; a < x < b , \;\; a,b, x \in R \} \] kümesi, \[ A= (a, \; b ) \] şeklinde gösterilir ve
A kümesine a sayısı ve, b sayısı dahil değildir anlamındadır.
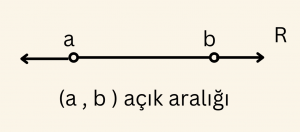
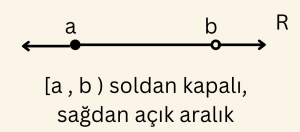
\[ A = \{ x | \; \; a ≤ x < b , \;\; a,b, x \in R \} \] kümesi, \[ A= [a, \; b ) \]
şeklinde gösterilir ve A kümesine a sayısı dahil b sayısı dahil değildir anlamındadır.
\[ A = \{ x | \; \; a < x ≤ b , \;\; a,b, x \in R \} \] kümesi, \[ A= (a, \; b ] \]
şeklinde gösterilir ve A kümesine a sayısı dahil değil b sayısı dahildir anlamındadır.

Örnekler:
\( \bullet \quad \) \( A = \{x : \;\;|x | ≤ 3, \;\; x \in R \}\) kümesi
\[ |x | ≤ 3 \Rightarrow -3 < x < 3 \;\; \text{olduğundan } A = [-3, 3 ] \]
\( \bullet \quad \) \( B = \{x : \;\;|x | ≤ 0, \;\; x \in R \}\) kümesi
\[ B = (- \infty, 0 ] \] şeklinde gösterilir.
Not: sonsuzluk kapanamaz dolayısı ile “(” kullanılır
← Önceki Sayfa | Sonraki Sayfa →