Matematik Sistemler
Bir küme ile bu küme üzerinde tanımlanmış bir veya daha çok işleme sistem adı verilir.
Örneğin tamsayılar kümesi ile \( +, . \) işlemleri
\[
(Z, +, .)
\]
bir sistem oluşturur.
Grup:
Boş olmayan bir \( A \) kümesi ile \( A \) üzerinde tanımlı bir \( \star \) işlemi verilsin.
1) \( A \), \( \star \) işlemine göre kapalı,
2) \( A \) üzerinde \( \star \) işleminin birleşme özelliği var,
3) \( A \) üzerinde \( \star \) işleminin birim elemanı var,
4) \( A \) üzerinde \( \star \) işlemine göre her elemanın tersi var
ise \( (A, \star) \) sistemi bir gruptur.
\( (A, \star) \) sistemi bir grup olsun. \( A \) üzerinde \( \star \) işleminin değişme özelliği varsa \( (A, \star) \) sistemi değişmeli gruptur.
Örnek:
\( Z / 5 = \{ 0, \overline{1}, \overline{2}, \overline{3}, \overline{4} \} \) kümesi üzerinde \( + \) işleminin tablosunu yapalım.
\[
\begin{array}{c|ccccc}
+ & 0 & \overline{1} & \overline{2} & \overline{3} & \overline{4} \\
\hline
0 & \overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4} \\
\overline{1} & \overline{1} & \overline{2} & \overline{3} & \overline{4} & \overline{0} \\
\overline{2} & \overline{2} & \overline{3} & \overline{4} & \overline{0} & \overline{1} \\
\overline{3} & \overline{3} & \overline{4} & \overline{0} & \overline{1} & \overline{2} \\
\overline{4} & \overline{4} & \overline{0} & \overline{1} & \overline{2} & \overline{3} \\
\end{array}
\]
\( Z / 5 \) kümesi üzerinde \( + \) işleminin;
1) Kapalılık,
2) Değişme,
3) Birleşme,
4) Birim eleman,
5) Ters eleman
özellikleri olduğundan \( (Z / 5, +) \) sistemi değişmeli gruptur.
Örnek:
Üçgen dönüşümleri:
1. Üçgenin başlangıç pozisyonu (0° döndürme)
2. Üçgenin saat yönünün tersine 120° döndürülmesi
3. Üçgenin saat yönünün tersine 240° döndürülmesi
Her dönüşüm bir grup elemanı olarak düşünülebilir.
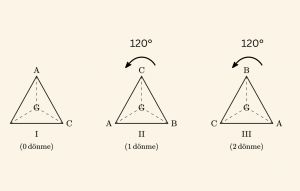
ABC eşkenar üçgeninin ağırlık merkezi \( G \) dir.
Üçgenin ilk hali \( (ABC) = I \), \( G \) etrafında ok yönünde \( 120^\circ \) dönmesi hali \( (CAB) = II \) ve bunun da \( 120^\circ \) dönmesi hali \( (BCA) = III \) olsun. \( 120^\circ \) lik dönme işlemini \( \star \) işlemi olarak alalım.
Burada,
\[
II \star III = I
\]
(1 dönme + 2 dönme = 3 dönme \( \Rightarrow \) 0 dönme) anlamındadır.
\[
A = \{ I, II, III \}
\]
kümesi üzerinde \( \star \) işleminin tablosunu yapalım.
\[
\begin{array}{c|ccc}
\star & I & II & III \\
\hline
I & I & II & III \\
II & II & III & I \\
III & III & I & II \\
\end{array}
\]
\( A \) kümesi üzerinde tanımlanan \( \star \) işleminin;
1) Kapalılık,
2) Değişme,
3) Birleşme,
4) Birim eleman,
5) Ters eleman
özellikleri olduğundan \( (A, \star) \) sistemi değişmeli gruptur.
Örnek:
\( (A, \circ) \) sistemi bir grup olsun. \( a, b, c, x \in A \) için,
\[
a \circ b \circ x = c
\]
ise \( x \) i bulalım.
\( (A, \circ) \) sistemi grup olduğundan \( \circ \) işleminin birleşme özelliği ve her elemanın tersi vardır.
\[
a \circ b \circ x = c \Rightarrow a^{-1} \circ a \circ b \circ x = a^{-1} \circ c
\]
\[
\Rightarrow e \circ b \circ x = a^{-1} \circ c \quad \text{ ( e birim eleman) }
\]
\[
\Rightarrow b \circ x = a^{-1} \circ c
\]
\[
\Rightarrow b^{-1} \circ b \circ x = b^{-1} \circ a^{-1} \circ c
\]
\[
\Rightarrow e \circ x = b^{-1} \circ a^{-1} \circ c
\]
\[
\Rightarrow x = b^{-1} \circ a^{-1} \circ c
\]
olarak bulunur.
Uyarı:
1) \( (A, \star) \) sistemi bir grup ise \( \forall x, y \in A \) için,
\[
(x \star y)^{-1} = y^{-1} \star x^{-1}
\]
2) Bir grubun işlem tablosunda bir satırda veya bir sütunda her eleman bir defa bulunur.
Örnek:
\[
A = \{ 1, 2, 3, 4 \}
\]
ve
\[
(A, \star) \text{ sistemi değişmeli gruptur.}
\]
a, b ve c harflerinin yerinde bulunması gereken elemanları bulalım.
\[
\begin{array}{c|cccc}
\star & 1 & 2 & 3 & 4 \\
\hline
1 & 2 & 3 & 4 & 1 \\
2 & 3 & a & b & 2 \\
3 & 4 & 1 & 2 & 3 \\
4 & 1 & 2 & 3 & c \\
\end{array}
\]
\( (A, \star) \) sistemi bir değişmeli gruptur. İkinci ve üçüncü sütunda her eleman bir defa bulunacağından
\[
a = 4, \quad b = 1
\]
dir.
Dördüncü satır (veya dördüncü sütunda) 4 elemanı yoktur. O halde
\[
c = 4
\]
tür.
Halka:
Boş olmayan bir \( A \) kümesi ile \( A \) da tanımlı \( \Delta \) ve \( \star \) işlemleri verilsin.
1) \( (A, \Delta) \) sistemi değişmeli grup,
2) \( A \) kümesi \( \star \) işlemine göre kapalı,
3) \( A \) kümesi üzerinde \( \star \) işleminin birleşme özelliği var,
4) \( A \) kümesi üzerinde \( \star \) işleminin \( \Delta \) işlemi üzerine dağılıma özelliği var,
ise \( (A, \Delta, \star) \) sistemi bir halkadır. \( A \) üzerinde \( \star \) işleminin birim elemanı varsa \( (A, \Delta, \star) \) sistemine birimli halka denir.
Cisim:
Boş olmayan bir \( A \) kümesi ile \( A \) da tanımlı \( \Delta \) ve \( \star \) işlemleri verilsin.
1) \( (A, \Delta, \star) \) sistemi birimli bir halka,
2) \( (A – \{0\}, \star) \) sistemi bir değişmeli grup,
ise \( (A, \Delta, \star) \) sistemi bir cisimdir.
Örnek:
\( \mathbb{Z} / 5 = \{ \overline{0}, \overline{1}, \overline{2}, \overline{3}, \overline{4} \} \) kümesi üzerinde ” + ” ve ” ⋅ ” işlemlerinin tablosunu yapalım.
\[
\begin{array}{c|ccccc}
+ & \overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4} \\
\hline
\overline{0} & \overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4} \\
\overline{1} & \overline{1} & \overline{2} & \overline{3} & \overline{4} & \overline{0} \\
\overline{2} & \overline{2} & \overline{3} & \overline{4} & \overline{0} & \overline{1} \\
\overline{3} & \overline{3} & \overline{4} & \overline{0} & \overline{1} & \overline{2} \\
\overline{4} & \overline{4} & \overline{0} & \overline{1} & \overline{2} & \overline{3} \\
\end{array}
\]
\[
\begin{array}{c|ccccc}
\cdot & \overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4} \\
\hline
\overline{0} & \overline{0} & \overline{0} & \overline{0} & \overline{0} & \overline{0} \\
\overline{1} & \overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4} \\
\overline{2} & \overline{0} & \overline{2} & \overline{4} & \overline{1} & \overline{3} \\
\overline{3} & \overline{0} & \overline{3} & \overline{1} & \overline{4} & \overline{2} \\
\overline{4} & \overline{0} & \overline{4} & \overline{3} & \overline{2} & \overline{1} \\
\end{array}
\]
\((\mathbb{Z} / 5, +) \) sistemi değişmeli grup,
\( A \) kümesi “\( \cdot \)” işlemine göre kapalı,
\( A \) kümesi üzerinde “\( \cdot \)” işleminin birleşme özelliği var,
\( A \) kümesi üzerinde “\( \cdot \)” işleminin “\( + \)” işlemi üzerine dağılıma özelliği var,
\( A \) kümesi üzerinde “\( \cdot \)” işleminin birim elemanı var.
O halde \( (A, +, \cdot) \) sistemi birimli halkadır.
Ayrıca,
\( (A – \{0\}, \cdot) \) sistemi bir değişmeli grup olduğundan \( (A, +, \cdot) \) sistemi cisimdir.
← Önceki Sayfa | Sonraki Sayfa →