Ondalık Sayılarda İşlemler
1. Toplama – Çıkarma:
Ondalık sayılar alt alta toplanırken (veya çıkarılırken) virgüller ve aynı isimli basamaklar alt alta gelecek şekilde yazılır. Doğal sayılarda olduğu gibi (virgül düşünülmeden) islem yapıldıktan sonra bulunan sonuç virgüller hizasından virgülle ayrılır.
Yanyana yapılan işlemlerde de sağdan sola doğru aynı isimli basamaklarda işlem yapılır ve onda birler basamağının soluna virgül yazılır.
Uyarı: Toplama veya çıkarma islemi yapılan sayıların kesir kısmındaki basamak sayıları eşit değilse, basamak sayısı eksik olan sayının sonuna sıfır yazılarak kesir kısmındaki basamak sayıları eşitlenir
Örnekler:
1) \( 217,72\) ve \( 16,4\) ve \( 3,215\) , sayılarını toplayalım.
\[\begin{align*}
&\phantom{+} &217,720 \\
&\phantom{+} &16,400 \\
+ &\phantom{+} &3,215 \\
\hline &\phantom{+} &237,335
\end{align*}
\]
veya
\[\begin{array}{l l }
217,720 + 16,400 + 3,215 = 237,335
\end{array}\]
2) \( 3,12 – 2,108\) işleminin sonucunu bulalım.
\[\begin{align*}
&\phantom{-} &3,120\\
-&\phantom{-} &2,108 \\
\hline &\phantom{-} &1,012
\end{align*}
\]
veya
\[\begin{array}{l l }
3,120 – 2,108 = 1,012 \quad bulunur
\end{array}\]
3) \( 1,7 – 1,92\) işleminin sonucunu bulalım.
\[\begin{array}{l l }
1,7 – 1,92 = 1,70 – 1,92 = -0,22 \quad olur
\end{array}\]
2. Çarpma:
iki ondalık sayıyı çarpmak için, çarpanlar virgülü yokmuş gibi düşünülerek çarpma işlemi yapılır. Bulunan çarpımda, çarpanların kesir kısımlarının basamak sayılarının toplamı kadar basamak (sağdan itibaren) virgülle ayrılır. Eksik basamaklar varsa yerine sıfır yazılır.
Örnek 1:
\[
\begin{align*}
3,84&\leftarrow \text{ 2 kesir basamaklı} \\
\times \quad 1,7&\leftarrow \text{ 1 kesir basamaklı} \\
\hline
\phantom{00}2688& \\
+ \phantom{0}384\phantom{0}& \\
\hline
6,528&\leftarrow \text{ 3 (= 2 + 1) kesir basamaklı}
\end{align*}
\]
Örnek 2:
\[
\begin{align*}
0,003&\leftarrow \text{ 3 kesir basamaklı} \\
\times \quad 4&\leftarrow \text{ 0 kesir basamaklı} \\
\hline
0,012&\leftarrow \text{ 3 kesir basamaklı}
\end{align*}
\]
Uyarı: Bir ondalık kesri 10 un kuvvetleri ile kolayca çarpmak için, ondalık kesrin virgülü, 10 un kuvveti olan sayıdaki sıfırlar kadar basamak sağa taşınır. Eksik basamaklar varsa yerine sıfır yazılır.
Örnekler:
- \[\begin{array}{l l } 1,15 \cdot 10 = \frac{115}{100} \cdot 10 = \frac{115}{10} =11,5 \\1, 15 \cdot 10= 11,5 \end{array}\]
- \[\begin{array}{l l } 100 \cdot 0,125 = 100 \cdot \frac{125}{1000} = \frac{125}{10} =12,5 \\ 100 \cdot 0, 125 = 0,12,5=12,5 \end{array}\]
3. Bölme:
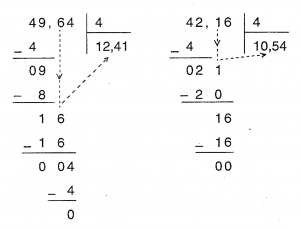
Bir ondalık kesri bu kesirden küçük bir sayma sayısına bölerken virgül yokmuş gibi bölme işlemi yapılır. Fakat işlem yapılırken sıra ondalık kesir basamağına (yani virgüle) geldiği zaman bölüme virgül konularak bölme işlemine devam edilir.
Örnekler:
49,64 :4 ve 42,16 : 4 işlemlerini yapalım.
Örnek:
2,16: 4 ve 3,24: 24 işlemlerini yapalım.
\[
\begin{array}{c,c}
\begin{array}{c}
\quad &2,16 \;\;\\
-\quad &2 \phantom{,} 0 \;\;\;\; \\
\hline
\;\;\quad &0\phantom{,} 16\\
-\quad \;\;\quad &0\phantom{,} 16\\
\hline
\;\;\quad &00\phantom{,}\\
\end{array}
\begin{array}{|c}
\quad 4 \\
\hline
\quad 0, 54
\\
\\
\\
\\
\end{array}
\end{array}
\]
\[
\begin{array}{c,c}
\begin{array}{c}
\quad &3,240 \;\;\\
-\quad &2 \phantom{,} 4 \;\;\;\; \\
\hline
\;\;\quad &0\phantom{,} 84\\
-\quad \;\;\quad \phantom{0} \phantom{,} &72\\
\hline
\;\;\quad &120\phantom{,}\\
-\;\;\quad &120\phantom{,}\\
\hline
\;\;\quad &00\phantom{,}\\
\end{array}
\begin{array}{|c}
\quad 24 \\
\hline
\quad 0, 135
\\
\\
\\
\\
\\
\\
\end{array}
\end{array}
\]
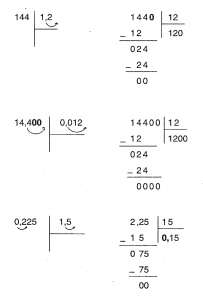
Bir bölme işleminde bölen ondalık kesir ise önce bölen 10 un uygun kuvveti ile çarpılarak virgülden kurtarılır. Bölünen de 10 un bu kuvveti ile çarpıldıktan sonra işlem yapılır.
Örnek:
144: 1,2 ; 14,4 : 0, 012 ve 0,225 :1,5 işlemlerini yapalım
Uyarı: Bir ondalık kesri 10 un kuvvetleri ile kolayca bölmek için, ondalık kesrin virgülü 10 un kuvvetindeki sıfırlar kadar basamak sola kaydırılır. Gerekirse, eksik basamaklar yerine sıfır yazılır.
Örnekler:
- $$ 43,8 :10 = 4,38$$
- $$ 21,7 :100 = 0,217$$
- $$ 2,72 :1000 = 0,00272$$
← Önceki Sayfa | Sonraki Sayfa →