Sayı Sistemleri

Konu İçeriği

Basamak ve Taban
Herhangi Bir Tabandaki Bir Sayının 10 Tabanında Yazılması
Sayı Sistemlerinde Tek ve Çift Sayılar
10 Tabanındaki Bir Sayının Herhangi Bir Tabanda Yazılması
Herhangi Bir Tabandaki Bir Sayının Başka Bir Tabanda Yazılması
a Tabanındaki Bir Sayının $a^n$ Tabanında Yazılması
Herhangi Bir Tabana Göre İşlemler

Basamak ve Taban:

Bir sayıda rakamların bulundukları yere basamak, sayıyı meydana getiren rakamların bulunduğu yerdeki değere basamak değeri ve bir sayı sisteminde sayının basamak değerlerini göstermek için kullanılan düzene de taban denir.

\[r_0, \; r_1, \; r_2, \; r_3, \; \dots, \; r_{n-1}, \; r_n\]
birer rakam ve $a$sayı tabanını göstermek üzere $a$ tabanındaki (a’lık sayma sistemindeki) $n + 1$ basamaklı $r_n, r_{n-1},\dots, r_2, r_1, r_0)_a$ sayısının basamakları

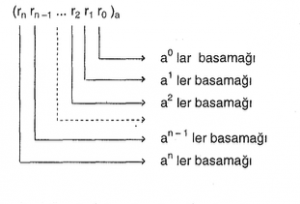
olmak üzere \[(r_n, r_{n-1}, \dots, r_2, r_1, r_0)_a\] sayısının

\[ r_n \cdot a^n + r_{n-1} \cdot a^{n-1} + \dots + r_2 \cdot a^2 + r_1 \cdot a^1 + r_0 \cdot a^0 \] şeklinde yazılışına bu sayının çözümlemiş şekli denir.

Örnek:

10 luk sistemdeki 1965 sayısını inceleyelim.

\[ \begin{array}{c c c c} 1 & 9 & 6 & 5 \\ \downarrow & \downarrow & \downarrow & \downarrow \\ 10^3 & 10^2 & 10^1 & 10^0 \\ \downarrow & \downarrow & \downarrow & \downarrow \\ 3 & 2 & 1 & 0 \\ \downarrow & \downarrow & \downarrow & \downarrow \\ 10^3 \, \text{binler basamağı} & 10^2 \, \text{yüzler basamağı} & 10^1 \, \text{onlar basamağı} & 10^0 \, \text{birler basamağı} \end{array} \]

1965 sayısında 1 rakamının basamak değeri bin, 9 rakamının basamak değeri dokuz yüz, 6 rakamının basamak değeri altmış, 5 rakamının basamak değeri beştir.

$$ 1965= 1\cdot10^3 + 9\cdot10^2 + 6\cdot10^1+ 5\cdot10^0$$

Örnekler:

$(3412)_5$ sayısının çözümlenmiş şekli

\[(3412)_5 = 3 \cdot 5^3 + 4 \cdot 5^2 + 1 \cdot 5^1 + 2 \cdot 5^0 \]

$(20000)_3$ sayısının çözümlemiş şekli

\[(20000)_3 = 2 \cdot 3^4\]

$(384,217)$ sayılarının çözümlemiş şekli

\[ 384,217 = 3 \cdot 10^2 + 8 \cdot 10^1 + 4 \cdot 10^0 + 2 \cdot 10^{-1} + 1 \cdot 10^{-2} + 7 \cdot 10^{-3} \]

Virgülden sonra basamak değerleri tabanın kuvvetine göre düşer, burada ki örnekte taban değeri 10 olduğundan değer de katları şeklinden düşer.

$(432,21)_5$ sayılarının çözümlemiş şekli

\[ (432,21)_5 = 4 \cdot 5^2 + 3 \cdot 5^1 + 2 \cdot 5^0 + 2 \cdot 5^{-1} + 1 \cdot 5^{-2} \]

Örnekler:

İki basamaklı ab ve aa sayıları

\[ ab = 10 \cdot a + b \]

\[ aa = 10 \cdot a + a = 11 \cdot a \]

Üç basamaklı abc ve aaa sayıları

\[ abc = 100 \cdot a + 10 \cdot b + c \] \[ aaa = 100 \cdot a + 10 \cdot a + a = 111 \cdot a \] Şeklinde çözümlenir.

Uyarı: Bir sayının basamaklarında yapılan bir işlemde, rakamların basamak değerleri göz önüne alınmalıdır. Örneğin bir sayının onlar basamağındaki rakamın sayısal değeri 3 artırılırsa sayının değeri 3.10 = 30 artar; bir sayının yüzler basamağındaki rakamın sayısal değeri 5 azaltılırsa sayının değeri 5 .100 = 500 azalır; bir sayının onlar basamağındaki rakam 7 artırılır, birler basamağındaki rakam 3 azaltılırsa sayının değeri 7.10 – 3.1 = 67 artar.

Örnek:

İki basamaklı bir sayının rakamlarının yerleri değiştirildiğinde bu sayının değeri 63 arttığına göre bu sayının rakamlarının farkinin mutlak degerini bulalım.

Bu iki basamaklı sayı ab olsun. Rakamlarının yerleri değiştirildiğinde elde edilen sayı ba olur. Bu sekilde sayının değeri 63 arttığına göre,

\[
\begin{align}
ba &= ab + 63 \\
\Rightarrow 10 \cdot b + a &= 10 \cdot a + b + 63 \\
\Rightarrow 9 \cdot |b – a| &= 63 \\
|b – a| &= 7 \text{ dir}
\end{align}
\]

Örnek:

İki basamaklı $ab$ sayısı ile bu sayının rakamlarının yerleri değiştirilerek elde edilen iki basamaklı $ab$ sayısı toplandığında sonuç 99 oluyor. Buna göre $ab$ sayısının en çok kaç olabileceğini bulalım.

\[ \begin{align} ab + ba &= 99 \Rightarrow 10 \cdot a + b + 10 \cdot b + a = 99 \\ \Rightarrow 11 \cdot (a + b) &= 99 \\ \Rightarrow a + b &= 9 \quad \text{olur.} \end{align} \]

$ab$ en büyük olacağına göre a en büyük olmalıdır. $a+b= 9$ oldugundan $a=9$, $b=0$ seçilirse $ba$ sayısı iki basamaklı sayı olmaz. Bu durumda $a=8$, $b =1$ seçilirse $ab$ nin en büyük degeri $81$ olarak bulunur.

Soru 14:

Rakamları tekrarsız, üç basamaklı, birbirinden farklı dört tane doğal sayının toplamı 768’dir.

Buna göre, en büyük sayı kaç olabilir?

\[ \text{A) } 458 \quad \text{B) } 459 \quad \text{C) } 460 \quad \text{D) } 461 \quad \text{E) } 462 \]

Çözüm:

En büyük sayıyı bulmak için diğer üç sayıyı en küçük olacak şekilde seçmeliyiz. Sayıların rakamları birbirinden farklı olduğuna göre, en küçük üç sayı $102$, $103$ ve $104$ olursa:

\[ \text{En büyük sayı } = 768 – (102 + 103 + 104) \]

\[ = 459 \text{ olarak bulunur.} \]

$\textbf{Cevab: B} $

Soru 15:

Dört basamaklı $abcd$ sayısının onlar ve binler basamağındaki rakamların yerleri değiştirildiğinde sayının değeri 5940 artıyor.

Buna göre, c – a farki kaçtır?

\[ \text{A) } 3 \quad \text{B) } 4 \quad \text{C) } 5 \quad \text{D) } 6 \quad \text{E) } 7 \]

Çözüm:

\[cbad= abcd + 6540 \quad olduğundan \] eşitliğin iki yanındaki sayılar çözümlenip düzenlenirse,

\[ \begin{aligned} 990 \cdot (c – a) &= 5940 \\
\Rightarrow c – a &= 6
\end{aligned}
\]

$\textbf{Cevab: D} $

Soru 16:

Üç basamaklı bir sayının sağına, bu sayı tekrar yazılarak altı basamaklı yeni bir sayı elde ediliyor.
Buna göre, elde edilen yeni sayı ilk sayının kaç katı fazla olur?

\[ \text{A) } 99 \quad \text{B) } 100 \quad \text{C) } 101 \quad \text{D) } 1000 \quad \text{E) } 1001 \]

Çözüm:

Sözü edilen iki sayı $abc$ ve $abcabc$ olsun.

\[\begin{aligned}
&abcabc – abc =x \cdot abc \\
&\Rightarrow abc000 = x . abc \\
&\Rightarrow x= 1000 \quad \text{kat daha fazladır}
\end{aligned}
\]

$\textbf{Cevab: D} $

Soru 17:

a, b ve c birbirinden farklı rakamlardır.

\[
\begin{array}{r}
\text{abc} \\
\text{bca} \\
+ \text{cab} \\
\hline 2109
\end{array}
\]

olduğuna göre, a + b + c toplamı kaçtır?

\[ \text{A) } 9 \quad \text{B) } 10 \quad \text{C) } 19 \quad \text{D) } 20 \quad \text{E) } 21 \]

Çözüm:

Verilen üç basamaklı sayıları çözümleyerek işlem yaparsak,

\[
\begin{array}{r}
100\cdot a + 10\cdot b + c \\
100\cdot a + 10\cdot b + c \\
+100\cdot a + 10\cdot b + c \\
\hline 111\quad \cdot( a+ b+ c)
\end{array}
\]
\[
\begin{aligned}
&111\quad \cdot( a+ b+ c)= {2109} \\
\\
&\Rightarrow a+b+c = \dfrac{2109}{111} = 19\quad dur
\end{aligned}\]

$\textbf{Cevab: C} $

Soru 18:

Her bir nokta ve a, b, c birer rakamın yerini tutmak üzere,

\[ \begin{array}{c@{}c}
\;\;\;\;ab\\
\times\;\;6c\\
\hline
\;\;…\\
+450\;\;\;\;\\
\hline
\;\;4725\\\
\end{array} \]

olduğuna göre, a + b + c toplamı kaçtır?

\[ \text{A) } 14 \quad \text{B) } 15 \quad \text{C) } 16 \quad \text{D) } 27 \quad \text{E) } 28 \]

Çözüm:

1. çarpan ile 6 nın çarpımı 450 olduğundan

\[ \begin{array}{c@{}c}
\;\;\;\;75 & \quad \text{I. çarpan} \\
\times\;\;\;6c &\quad \text{II. çarpan} \\
\hline
\;\;xyz\\
+\;\;450\;\;\;\;\\
\hline
\;\;4725\\\
\end{array} \]

\[
\begin{array}{c@{}c}
\;\;\;\;\;\;xyz& \\
+\;\;\;4500 &\\
\hline
\;\;\;\;4725\\
\\
\\
xyz = 4725 – 4500 \Rightarrow xyz = 225 \quad \text{elde edilir. O halde,} \\
75 \cdot c = xyz = 225 \Rightarrow c = \dfrac{225}{75} \Rightarrow c = 3 \quad \text{bulunur.} \\
ab = 75 \quad \text{olduğuna göre} \quad a = 7, \quad b = 5 \quad \text{olur.} \\
\text{Dolayısıyla } \quad a + b + c = 7 + 5 + 3 = 15 \quad \text{tir.}
\end{array}
\]

$\textbf{Cevab: B} $

Soru 19:

xyz üç basamaklı bir doğal sayıdır. $x = y + 2$ ve $y = z + 2$ şartlarına uygun olarak yazılabilecek tek sayıların toplamı kaçtır?

\[
\text{A) 2159} \quad \text{B) 2259} \quad \text{C) 2616} \quad \text{D) 2915} \quad \text{E) 3210}
\]

Çözüm:

Verilen şartlara göre, x ve y rakamları, z için seçebileceğimiz değerlere bağlıdır.
z tek sayı olmak şartıyla, z için seçebileceğimiz değerlere göre verilen şartlarda yazılabilecek üç basamaklı sayılar yazılıp toplama işlemi yapılırsa; (z 1,3 ve 5 olabilir. 5 ten büyük değerler x ve y değerlerini rakam olmaktan çıkarır)

\[
531 + 753 + 975 = 2259
\]

$\textbf{Cevab: B} $

Soru 20:

a ≠ b olmak üzere, abb ve baa üç basamaklı doğal sayılar olduğuna göre, $\dfrac{abb – baa}{b – a}$ kesrinin değeri kaçtır?

\[\text{A) 89 B) -89 C) 91 D) -91 E) 101}\]

Çözüm:

\[
\frac{abb – baa}{b – a} = \frac{100a + 10b + b – (100b + 10a + a)}{b – a} \\
= \frac{89a – 89b}{b – a} \\
= \frac{89 \cdot (a – b)}{b – a} = 89 \times \frac{a – b}{b – a} = -89 \text{ dur.}
\]

$\textbf{Cevab: B} $

Soru 21:

2mn4 ve 1mn7 dört basamaklı doğal sayılar olmak üzere

\[ \begin{array}{r} 2mn4 \\ – 1mn7 \\ \hline \cdots \end{array} \]

çıkarma işleminin sonucu kaçtır?

\[\text{A) 1004 B) 1003 C) 997 D) 907 E) 903}\]

Çözüm:

Verilen sayılar çözümlenerek çıkarma işlemi yapılırsa,

\[ \begin{array}{r} 2000 +100m +10n + 5 \\ -1000 + 100m +10n+ 7 \\ \hline 1000-3 =997\quad \text{bulunur.} \end{array} \]

$\textbf{Cevab: C} $

Soru 22:

a ve b birer rakamdır.

\[ \begin{array}{r} ab3 \\ – ab \\ \hline 408 \end{array} \]

olduğuna göre $a.b$ çarpımı kaçtır?

\[\text{A) 15 B) 18 C) 20 D) 24 E) 25}\]

Çözüm:

1. Yol

Verilen sayılar çözümlenerek çıkarma işlemi yapılırsa

\[
\begin{array}{l}
100\cdot a + 10\cdot b + 3 – (10+b) =408\\
\Rightarrow 90\cdot a + 9\cdot b =405 \\
\Rightarrow 9\cdot (10\cdot a + b) =405\\
\Rightarrow ab=45 \text{olur. Buna göre,}\\
a=4, \quad b= 5 \quad ve \quad a\cdot b= 20 \text{ dir}
\end{array}
\]

2. Yol

\[ \begin{array}{l} ab3 \\ – ab \\ \hline 408 \end{array} \]

Birler basamağındaki işleme dikkat edilirse b‘nin 3’ten büyük olduğu görülür. Buna göre, 3’ten b çıkmayacağına göre onlar basamağındaki b‘den 1 alınıp birler basamağındaki 3’e, bir onluk olarak ilâve edilirse 13 olur. Bu durumda 13 – b = 8 çıkarma işleminden b = 5 bulunur. Onlar basamağındaki işlem yapılırsa; b‘den 1 alındığı için geriye b – 1 kalır. (b – 1) – a = 0 işleminden 5 – 1 = a = 4 elde edilir.

Buna göre, a . b çarpımı 20 olarak bulunur.

$\textbf{Cevab: E} $

Soru 23:

Bir öğrenciden, verilen üç basamaklı bir sayı ile 75’in çarpımını hesaplaması istenmiştir. Öğrenci işlemin sonucunu 8850 olarak bulmuştur. Bu öğrencinin yaptığı işlemi kontrol eden öğretmeni, öğrencinin işlemi yaparken verilen üç basamaklı sayının onlar basamağındaki 7 rakamını 1 zannederek hesap yapmış olduğunu tespit etmiştir.

Buna göre, verilen çarpma işleminin doğru sonucu kaçtır?

\[\text{A) 9300 B) 9750 C) 10500 D) 11400 E) 13350}\]

Çözüm:

1. Yol

Öğrenci, verilen üç basamaklı sayının onlar basamağındaki 7 rakamını 1 zannettiği için bulduğu sonuç, gerçek sonuçtan

\[
\begin{array}{l}
(7-1)\cdot 10 \cdot 75 =4500 \text{ daha azdır. Buna göre doğru sonuç}\\
8850 +4500=13350 \text{ dir.}\\
\end{array}
\]

2. Yol

Ögrencinin okuduğu üç basamaklı sayı x olsun. Buna göre ögrencinin yaptığı işlem

$$x\cdot 75=8850 \quad ise \quad x=118\quad dir.$$

O halde ögrenciye verilen çarpma islemi $178 \cdot 75$ tir. Bu islemin doğru sonucu 13350 dir.

$\textbf{Cevab: E} $

Uyarı:

a sayıyı tabanını, x, y ve z de a tabanındaki rakamları göstermek üzere,

(xyz)ₐ ifadesi a tabanında (a’lı sayma sisteminde) üç basamaklı bir sayıyı gösterir ve a sayısı 1’den ve x, y, z rakamlarından büyüktür.

En küçük tabanlı sayma sistemi 2’lik sayma sistemidir.
a tabanında kullanılan rakamlar a tanedir ve en büyük rakam a – 1‘dir.
10’luk sistemde yazılan sayılarda tabanı yazmaya gerek yoktur.

Örnek:

2 tabanında kullanılan rakamların kümesi {0, 1}
5 tabanında kullanılan rakamların kümesi {0, 1, 2, 3, 4}
10 tabanında kullanılan rakamların kümesi {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
12 tabanında kullanılan rakamların kümesi {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B} ve burada A’nın değeri 10, B’nin değeri 11’dir.

Herhangi Bir Tabandaki Bir Sayının 10 Tabanında Yazılması

Herhangi bir tabandaki bir sayı, çözümlenmek suretiyle 10 tabanındaki eşiti bulunur.

$(118)_9$, $(1034)_5$, $(21203)_4$, $(101101)_2$s h sayılarının 10 tabanındaki eşitini bulalım.

\[ (118)_9 = 1\cdot 9^2+ 1\cdot 9^1 + 8\cdot 9^0 =98 \]

\[ (1034)_5 = 1\cdot 5^3+ 0\cdot 5^2 + 3\cdot 5^1 + 4\cdot 5^0 =144 \]

\[ (21203)_4 = 2\cdot 4^4+ 1\cdot 4^3 + 2\cdot 4^2+0\cdot 4^1+3\cdot 4^0 =611 \]

\[ (101101)_2 = 1\cdot 2^5 + 0\cdot 2^4 + 1\cdot 2^3 + 1\cdot 2^2+0\cdot 2^1+1\cdot 2^0= 45\]

$(110,01)_2$ ve $(123,21)_4$ sayılarının 10 lu tabanındaki eşitini bulalım.

\[ (110,01)_2 = 1\cdot 2^2+ 1\cdot 2^1 + 0\cdot 2^0 + 0\cdot 2^{-1}+ 1\cdot 2^{-2}= 4+2+\dfrac{1}{4}=\dfrac{25}{4}=6,25\]

\[ (123,21)_4 = 1\cdot 4^2+ 2\cdot 4^1 + 3\cdot 4^0 + 2\cdot 4^{-1}+ 1\cdot 4^{-2}= 27+2\cdot{1}{4}+\dfrac{1}{16}= 27,5625\]

Soru 24:

x sayı tabanını göstermek üzere, $(132)_x=42$ olduğuna göre, x kaçtır?

\[\text{A) 8 B) 7 C) 6 D) 5 E) 4}\]

Çözüm:

\[
\begin{array}{l}
(132)_x=42\\
\Rightarrow 1\cdot x^2 + 3\cdot x^1 + 2\cdot x^0 =42\\
\Rightarrow (x^2+ 3)\cdot (x-40)=0\\
\Rightarrow (x-5)\cdot(x+8)=0\\
\Rightarrow x-5=0 \quad veya \quad x+8 = 0 \\
x= 5 \quad veya \quad x=-8\\
\text{x sayı tabanı olduğuna göre, } x=5 \quad tir
\end{array}
\]

$\textbf{Cevab: D} $

Soru 25:

x sayı tabanını göstermek üzere, $(43)_x+(36)_x=(101)_x$ olduğuna göre, x kaçtır?

\[\text{A) 7 B) 8 C) 9 D) 10 E) 11}\]

Çözüm:

\[
\begin{array}{l}
\Rightarrow (4x^1+3) + (3x^1+6)= (x^2+x^1\cdot0+1)\\
\Rightarrow x^2-7x-8=0\\
\Rightarrow (x-8)\cdot (x+1)=0\\
\text{buradan} x=8 \quad veya x=-1\\
\text{x sayı tabanı olduğundan x = 8 olmalıdır}
\end{array}
\]

$\textbf{Cevab: B} $

Sayı Sistemlerinde Tek ve Çift Sayılar

a tabanındaki n + 1 basamaklı R = (rₙ rₙ₋₁ … r₂ r₁ r₀)ₐ sayısı için,

a çift sayı iken r₀ çift sayı ise R de çift, r₀ tek sayı ise R de tek sayıdır.
a tek sayı iken r₀ + r₁ + r₂ + … + rₙ toplamı tek sayı ise R de tek, çift sayı ise R de çift sayıdır.

Örnekler:

• $(10010)_2$, $(3214)_6$ ,$(12302)_4$ 384 sayıları çift

• $(101001)_2$, $(43213)_6$ ,$(30221)_4$ 217 sayıları tek sayıdır.

• 1+2+1+4 =8 çift sayı olduğundan $(1214)_5$ sayısı çift, 1 + 0 + 2 = 3 tek sayı olduğundan $(102)_3$ sayısı tek sayıdır.

10 Tabanındaki Bir Sayının Herhangi Bir Tabanda Yazılması

10 tabanında verilen bir sayı istenen tabana çevrilirken, verilen sayı istenen tabana bölünür. Elde edilen bölüm istenen tabandan küçük değilse, bulunan bölüm tekrar istenen tabana bölünür. Bu işlem, istenen tabandan küçük bir bölüm elde edilene kadar arka arkaya sürdürülür.

İstenen tabandan küçük bir bölüm elde edildiğinde, bu bölüm ve önceki bölmelerde elde edilen kalanlar, sonuncudan başlayarak geriye doğru sıralanarak istenen tabandaki sayının rakamlarını oluşturur.

Örnek:

124 sayısının 4 tabanındaki eşitini bulalım. $124 = (1330)_4$

\[
\begin{array}{l}
\text{1. Adım: } 124 \div 4 = 31 \quad \text{Kalan: } 0 \\
\text{2. Adım: } 31 \div 4 = 7 \quad \text{Kalan: } 3 \\
\text{3. Adım: } 7 \div 4 = 1 \quad \text{Kalan: } 3 \\
\text{4. Adım: } 1 \div 4 = 0 \quad \text{Kalan: } 1 \\
\text{Aşağıdan yukarı doğru kalanlar yazılırsa: }
\text{Sonuç: } 124_{10} = (1330)_4
\end{array}
\]

Örnek:

11 sayısının 2 tabanındaki eşitini bulalım.

\[
\begin{array}{l}
\text{1. Adım: } 11 \div 2 = 5 \quad \text{Kalan: } 1 \\
\text{2. Adım: } 5 \div 2 = 2 \quad \text{Kalan: } 1 \\
\text{3. Adım: } 2 \div 2 = 1 \quad \text{Kalan: } 0 \\
\text{4. Adım: } 1 \div 2 = 0 \quad \text{Kalan: } 1 \\
\text{Aşağıdan yukarı doğru kalanlar yazılırsa: }
\text{Sonuç: } 11_{10} = (1011)_2
\end{array}
\]

Soru 26:

3975 sayısının 11 tabanındaki yazılışı $(abcd)_11$ dir. Buna göre, a +b +c +d toplamanın 11 tabanındaki eşiti nedir?

\begin{array}{ll} \text{A) } (25)_{11} & \text{B) } (23)_{11} \\ \text{C) } (52)_{11} & \text{D) } (32)_{11} \\ \text{E) } (A1)_{11} \end{array}

Çözüm:

\[
\begin{array}{l}
\text{1. Adım: 3975 sayısını 11 tabanına çevirelim:}\\
\\
3975 \div 11 = 361 \quad \text{Kalan: } 4 \quad (d = 4) \\
361 \div 11 = 32 \quad \text{Kalan: } 9 \quad (c = 9) \\
32 \div 11 = 2 \quad \text{Kalan: } 10 \quad (b = A) \\
2 \div 11 = 0 \quad \text{Kalan: } 2 \quad (a = 2) \\
\text{Bu işlemler sonucunda:} \\
3975_{10} = (2A94)_{11}\\
\\
\text{2. Adım: } a + b + c + d \text{ toplamını bulalım:}\\
\\
a + b + c + d = 2 + 10 + 9 + 4 = 25\\
\text{3. Adım: Bu toplamı 11 tabanına çevirelim:}\\
25 \div 11 = 2 \quad \text{Kalan: } 3 \\
\text{Sonuç: } 25_{10} = (23)_{11}\\
\end{array}
\]

$\textbf{Cevab: B} $

Herhangi Bir Tabandaki Bir Sayının Başka Bir Tabanda Yazılması

Herhangi bir tabanda verilen bir sayı çözümlenerek 10 tabanındaki eşiti bulunur. Daha sonra 10 tabanından istenen tabana çevrilir.

Örnekler:

• $(1011101)_2$ sayısının 3 tabanındaki eşitini bulalım.

\[
\begin{array}{l}
(1011101)_2= 1\cdot2^6+0\cdot2^5+1\cdot2^4+1\cdot2^3+1\cdot2^2+0\cdot2^1+1\cdot2^1\\
=64+16+8+4+1=93\\
(1011101)_2=93\quad olur.\\
\\
\text{93 sayısını 3 lük tabana çevirdiğimizde}\\
\\
1. \quad 93 \div 3 = 31 \quad \text{bölüm}, \quad \text{kalan} = 0\\
2. \quad 31 \div 3 = 10 \quad \text{bölüm}, \quad \text{kalan} = 1\\
3. \quad 10 \div 3 = 3 \quad \text{bölüm}, \quad \text{kalan} = 1\\
4. \quad 3 \div 3 = 1 \quad \text{bölüm}, \quad \text{kalan} = 0\\
5. \quad 1 \div 3 = 0 \quad \text{bölüm}, \quad \text{kalan} = 1\\
\\
(10110)_3 \quad bulunur
\end{array}
\]
olduğundan $(1011101)_2 =93=(10110)_3$ olur

• $(123)_4$ sayısının 5 tabanındaki eşitini bulalım.

\[
\begin{array}{l}
(123)_4= 1\cdot4^2+2\cdot4^1+3\cdot4^0\\
=16+8+1=27\\
(123)_4=27\quad olur.\\
\text{27 sayısını 5 lik tabana çevirdiğimizde}\\
\\
1. \quad 27 \div 5 = 5 \quad \text{bölüm}, \quad \text{kalan} = 2\\
2. \quad 5 \div 5 = 1 \quad \text{bölüm}, \quad \text{kalan} = 0\\
3. \quad 1 \div 5 = 0 \quad \text{bölüm}, \quad \text{kalan} = 1\\
27 = (102)_5
\end{array}
\]
olduğundan $(123)_4 =27=(102)_5$ olur

a Tabanındaki Bir Sayının $a^n$ Tabanında Yazılması

a tabanında verilen bir sayı $a^n$ tabanında yazılırken:

1. Verilen sayının basamakları sağdan sola doğru n`li gruplara ayrılır.
2. En soldaki gruptan başlayarak her bir grup sırasıyla a tabanına göre çözümlenerek $a^n$ tabanında yazılacak sayının rakamları bulunur.
3. Bulunan rakamlar sırasıyla soldan sağa doğru yazılarak a tabanındaki sayının $a^n$ tabanındaki eşiti elde edilir.

Örnekler:

• $ (10110011010)_2 $ sayısının 8 tabanındaki eşitini bulalım.

$8=2^3$ olduğundan $(10110011010)_2$ sayısının basamaklarını sağdan sola doğru 3 erli gruplara ayırarak her grubu 2 tabanına göre sırasıyla soldan sağa doğru çözümleyelim.

\[
\begin{array}{l}
(10 \quad110 \quad011 \quad010)_2 = (abcd)_8 \quad olsun\\
(10)_2=2=a\\
(110)_2=6=b\\
(011)_2=3=c\\
(010)_2=1=d \quad olduğundan\\(10110011010)_2=(2632)_8\quad olur.
\end{array}
\]

•$(2012201)_3$ sayısının 9 tabanındaki eşitini bulalım.

$9=3^2$ olduğundan $(2012201)_3$ sayısının basamaklarını sağdan sola doğru 2 erli gruplara ayırarak her grubu 3 tabanına göre sırasıyla soldan sağa doğru çözümleyelim.

\[
\begin{array}{l}
(2\quad 01\quad 22\quad 01)_3 = (abcd)_9 \quad olsun\\
(2)_3=2=a\\
(01)_3=1=b\\
(22)_3=8=c\\
(01)_3=1=d \quad olduğundan\\
(2 01 22 01)_3=(2181)_9 \quad olur.
\end{array}\]

$(101010100111010101)_2$ sayısının 16 tabanındaki eşitini bulalım.

$16 = 2^4$ olduğundan $$(101010100111010101)_2$$ sayısının basamaklarını sağdan sola doğru 4 erli gruplara ayırıp her grubu sırasıyla soldan sağa doğru çözümleyelim.

\[
\begin{array}{l}
(101010100111010101)_2 = (abcde)_{16} \quad \text{olsun}\\
\\
\text{Dörtlü gruplara ayırıyoruz:} \\
(101010100111010101)_2 = (10\ 1010\ 1001\ 1101\ 0101)_2 \\
\\
(10)_2 = 2_{16}=a\\
(1010)_2 = 10_{16}=b=A\\
(1001)_2 = 9_{16}=c\\
(1101)_2 = 13_{16}=d=D\\
(0101)_2 = 5_{16}=e\\
\\
(101010100111010101)_2 = (2A9D5)_{16} \quad \text{olur.}
\end{array}
\]

Soru 27:

5 tabanındaki rakamları birbirinden farklı dört basamaklı en büyük tek sayının 4 tabanındaki eşiti nedir?

\begin{array} \text{A) } (2203)_{4} & \text{B) } (3011)_{4}& \text{C) } (3201)_{4} & \text{D) } (21021)_{4}& \text{E) } (20121)_{4} \end{array}

Çözüm:

Verilen şartlara uygun 5 tabanındaki sayı $(abcd)_5$ olsun. Bu sayı tek sayı olacağından a+b+c+d toplamı tek sayı olmalıdır. Buna göre a=4, b = 3, c=2, d = 0, seçilirse $(4320)_5$ olur. Bu sayının 4 tabanındaki eşitini bulmak için önce 10 tabanına çevirelim.

\[
\begin{array}{l}
(4320)_5= 4\cdot 5^3 + 3\cdot 5^2 + 2\cdot 5^1 + 0\cdot 5^0 =585 \\
\text{585 sayısını 4 tabanına çevirirsek}\\
\\
585 \div 4 = 146 \quad \text{kalan} \ 1 \\
146 \div 4 = 36 \quad \text{kalan} \ 2 \\
36 \div 4 = 9 \quad \text{kalan} \ 0 \\
9 \div 4 = 2 \quad \text{kalan} \ 1 \\
2 \div 4 = 0 \quad \text{kalan} \ 2 \\
\\
\text{Kalanları tersten yazarsak:} \\
585 = (21021)_4
\end{array}
\]

$\textbf{Cevab: D} $

Soru 28:

16 Sayı tabanı olmak üzere $(5A2)_{16}$ sayısının 2 tabandaki eşiti nedir.

\begin{array} \text{A) } (101101010)_{2} & \text{B) } (10110100010)_{2}& \text{C) } (111010010)_{2} & \text{D) } (1010101011)_{2}& \text{E) } (1100110101)_{2} \end{array}

Çözüm:

$(5A2)_{16}$ sayısının rakamlarını soldan sağa sırasıyla 2 tabanına çevirip bulduğumuz değerleri ayni sırada yerine yazarsak $(5A2)_{16}$ sayısının 2 tabanındaki eşitini bulabiliriz. Burada $16 = 2^4$ olduğundan bu sayının rakamlarını 2 tabanına çevirdiğimizde elde edilen değerler 4 rakamdan meydana gelmelidir.

Buna göre işlem yapılırsa,

\[
\begin{array}{l}
(5A2)_{16}\\
5=(101)_2=(0101)_2\\
A=10=(1010)_2\\
2=(10)_2=(0010)_2 \text{ elde edilir.}
\end{array}
\]

Bu değerler sırasıyla soldan sağa doğru yazılırsa $(010110100010)_2$ sayının en solundaki sıfır (0) sayının değerini değiştirmez. O halde $(5A2)_{16}$sayısının 2 tabanındaki eşiti $(010110100010)_2$ olur.

$\textbf{Cevab: B} $

Soru 29:

16 sayı tabanını göstermek üzere, $(5A93C2)_{16}$ sayısının 2 tabandaki eşiti kaç basamaklıdır.

\begin{array} \text{A) } 16 & \text{B) } 21 & \text{C) } 23 & \text{D) } 24 & \text{E) } 26 \end{array}

Çözüm:

$16=2^4$ olduğundan $(5A93C2)_{16}$ sayısının rakamlarının her biri (5 hariç) bu sayının 2 tabanındaki eşitinin basamaklarının sağdan sola doğru 4 erli gruplara ayrılıp 2 tabanında çözümlenmesiyle elde edilmiştir. Buna göre 2, C, 3, 9, A rakamlarının her biri için 4 basamak sayılmalıdır. $5= (101)_2$ olduğundan 5 rakamı da 3 basamağa karşılık gelir. O halde $(5A93C2)_{16}$ sayısının 2 tabanındaki karşılığı $5\cdot 4+ 3 = 23$ basamaklıdır.

$\textbf{Cevab: E} $

Herhangi Bir Tabana Göre İşlemler

Ayni tabana göre yazılmış iki sayının toplamı, çarpımı ve farki 10 tabanına göre yapılan işlemlere benzer işlemlerle bulunur. Fakat göz önüne alınması gereken iki durum vardır.

Birincisi, toplama ve çarpma islemi yapılırken islem süresince ortaya çıkan sayılarda taban değerinin katları elde olarak bir sonraki isleme eklenir.
İkincisi ise çıkarma işlemi yapılırken gerektiğinde bir soldaki basamaktan 1 (bir) alındığı taktirde bu 1 in aktarıldığı basamağa katkısı tabanın değeri kadardır.

Örnekler:

$(2)_6 + (3)_6=(5)_6$
$(31)_6 + (14)_6=(45)_6$
$(3)_6+(3)_6=(10)_6$

Açıklama: 3+3 =6 olur. 6 tabanında 6 yazılamayacağından 6 içinde kaç tane 6 olduğuna bakılır. 6 da 6 bir kere var. O halde elde 1 vardır. 6 dan elde olan 1 tane 6 çıkarılırsa geriye 0 kalır. Geriye kalan bu 0 birler basamağına yazılır. Eldeki 1 de bir sonraki basamağa yani 6 lar basamağına katılır. Baska islem olmadığından 6 lar basamağında sadece 1 bulunur. Buna göre $(3)_6+(3)_6=(10)_6$. Başka bir örneğe bakalım;

\[ \begin{array}{c@{}c@{}c@{}c@{}c@{}c}
(3214)_6\\
+(235)_6\\
\hline
(3453)_6
\end{array} \]

Birler basamağındaki 4 ile 5 toplanırsa 9 eder. 9, 6’dan büyük olduğundan 9’u 6’ya bölersek; 9’da 6 bir kere vardır. O halde elde 1 olur. 9’dan eldeki 1 tane 6 çıkarılırsa geriye kalan 3 birler basamağına yazılır. Elde kalan 1 ise 6’lar basamağındaki işleme 1 olarak eklenir. 6 lar basamağındaki 1 ile 3 toplanırsa 4 olur. Eldeki 1 de 4e eklenirse 5 olur. Bu 5,6 dan küçük olduğu için aynen 6 lar basamağına yazılır. Bu şekilde diğer basamaklarda da ayni işlemler yapılır.

Çarpma işlemi

\[ \begin{array}{c@{}c@{}c@{}c@{}c@{}c}
(343)_5\\
\times(34)_5\\
\hline
\;\;\;\;\;\;(3032)_5\\
+(2134)_5\\
\hline
\;\;\;\;\;\;(24422)_5\\
\end{array} \]

Açıklama: $4 . 3 = 12 = (22)_5$ işlemi sonunda bulunan birler basamağındaki 2 birler basamağına yazıldı ve 5 ler basamağındaki 2 elde olarak $4 . 4 = 16$ sonucuna eklenip $18 = (33)_5$ bulundu; buradaki birler basamağındaki 3 beşler basamağına yazıldı, beşler basamağındaki 3 ise elde olarak $4. 3 = 12$ sonucuna eklenip $15 = (30)_5$ bulundu. Buradaki 0 (sıfır) yirmi beşler basamağına yazıldı ve beşler basamağındaki 3 elde olarak (başka bir işlem yapılmadığından yüz yirmi, beşler basamağına yazılarak $(343)_5.(4)_5 = (3032)_5$ elde edildi.

Benzer işlemler yapılarak da

$$(343)_5\cdot(3)_5 = (2134)_5$$

bulundu. 10 tabanındaki işlemlerde olduğu gibi ikinci çarpma işleminin sonucu, birincinin altına yazılırken sağdan bir basamak sola kaydırılarak yazıldı ve bu iki sonuç toplanarak $(343)_5\cdot (34)_5$ çarpma işleminin sonucu $(24422)_5$ olarak bulundu.

İki örnek daha yapacak olursak;

\[ \begin{array}{c@{}c@{}c@{}c@{}c@{}c}
\;\;(101101)_2\\
\;\;\times\;\;(101)_2\\
\hline
\;\;(101101)_2\\
+(101101)_2\;\;\;\;\;\;\;\;\;\\
\hline
\;\;(11100001)_2\\\
\end{array} \]

\[ \begin{array}{c@{}c@{}c@{}c@{}c@{}c}
\;\;(3454)_6\\
\times\;\;(345)_6\\
\hline
\;\;(31042)_6\\
(23144)_6\;\;\;\\
\;\;+(15250)_6\;\;\;\;\;\;\;\;\;\;\;\\
\hline
(2231522)_6\;\;\;\;\\\
\end{array} \]

Çıkarma işlemi

\[ \begin{array}{c@{}c@{}c@{}c@{}c@{}c}
\;\;(30324)_5\\
-(12343)_5\\
\hline
\;\;(12431)_5\\
\end{array} \]

Açıklama: Birler basamağında 4 – 3 = 1 sonucu birler basamağına yazılır. Beşler basamağındaki 2 den 4 çıkarıldığına göre bir soldan (yirmi beşler basamağından) 1 alınarak (değeri 5 olduğundan) 2 ye eklenirse 2+5=7 olur. 7-3=4 sonucu beşler basamağına yazılır. Yirmi beşler basamağındaki 3 ten 1 alındığı için geriye 2 kalmıştır. 2 den 3 çıkmayacağından bir soldaki basamaktan, orada da 0 olduğundan onun solundaki basamaktan (altı yüz yirmi beşler basamağından) bir tane bir alınıp bir sağa (yüz yirmi beşler basamağına) aktarılıp buradaki sıfıra eklenirse (1 in değeri 5 olduğu için) 5 olur. Bu 5 ten de 1 alınıp bir sağa (yirmi beşler basamağına) aktarılıp burada kalan 2 ile toplanırsa (1 in değeri 5 olduğundan) 7 eder. 7 – 3 = 4 sonucu yirmi beşler basmağına yazılır.Yüz yirmi beşler basamağındaki 5 ten (altı yüz yirmi beşler basamağından alınan 5 ten) 1 alındığı için geriye kalan 4 ten 2 çıkarılırsa 4 – 2 = 2 olur. Bu sonuç yüz yirmi beşler basamağına yazılır. En soldaki 3 ten 1 alınıp sağa aktarıldiğı için geriye kalan 2 den 1 çıkarılırsa 2 – 1 = 1 sonucu da altı yüz yirmi beşler basamağına yazılır.

\[
\begin{array}{c@{\quad}c@{\quad}}
\begin{array}{r}
\;\;(6543)_7 \\
-(2343)_7 \\
\hline
\;\;(4200)_7 \\
\end{array}
&
\begin{array}{r}
\;\;(1234)_5 \\
-(321)_5 \\
\hline
\;\;(0413)_5 \\
\end{array}
&
\begin{array}{r}
\;\;(53C47)_{15} \\
-(4A35)_{15} \\
\hline
\;\;(4E212)_5 \\
\end{array}
\end{array}
\]

Bölme işlemi

10 tabanında olduğu gibi bölünen sayı içerisinde bölüm araştırılırken bölünenin basamaklarına soldan sağa doğru bakılmalı ve bölünen ile bölen in 10 tabanındaki değerlerine göre bölüm tespit edilip bundan sonraki çarpma ve çıkarma işlemi bölme yapılan tabana göre yapılmalıdır.

Yada bölen ve bölünen 10`luk tabana çevrilir ve bildiğimiz bölme işlemi yapılır ve sonuç istenen tabana çevrilir.

Örnek:

Verilen bölme işlemi: $(41)_5 \div (12)_5$ olsun\[
\begin{array}{c@{\quad}c@{\quad}}
\textbf{Adım 1: Sayıları Onluk Sisteme Çevirme}\\
\\
(41)_5 = 21\\
(12)_5 = 7\\
\\
\textbf{Adım 2: Onluk Sistemde Bölme İşlemi}\\
\\
21\div7=3\\
\\
\textbf{Adım 3: Sonucu Taban 5’e Çevirme ve Kontol}\\
\\
\text{Sonuç 3 hem 10 hem de 5 tabanında aynı değere sahip olduğundan herhangi bir dönüşüm uygulanmaz}\\
(12)_5\cdot(3)_5=(41)_5
\end{array}
\]

Örnek:
Verilen bölme işlemi: $(114332)_5 \div (23)_5$ olsun
\[
\begin{array}{c@{\quad}c@{\quad}}
\textbf{Adım 1: Sayıları Onluk Sisteme Çevirme}\\
\\
(114332)_5 \div (23)_5
\end{array}
\]

Öncelikle, sayıları taban 10’a çevirelim:

Bölen:
\[
(23)_5 = 2 \times 5^1 + 3 \times 5^0 = 10 + 3 = 13_{10}
\]

Bölünen:
\[
(114332)_5 = 1 \times 5^5 + 1 \times 5^4 + 4 \times 5^3 + 3 \times 5^2 + 3 \times 5^1 + 2 \times 5^0
\]
\[
\begin{array}{c@{\quad}c@{\quad}}
= 3125 + 625 + 500 + 75 + 15 + 2 = 4342_{10}\\
\\
\textbf{Adım 2: Onluk Sistemde Bölme İşlemi}\\
\end{array}
\]

\[
4342 \div 13 = 334
\]

\[
\begin{array}{c@{\quad}c@{\quad}}
\textbf{Adım 3: Sonucu Taban 5’e Çevirme}\\
\\
334_{10} = 2 \times 5^3 + 3 \times 5^2 + 1 \times 5^1 + 4 \times 5^0 = (2314)_5\\
\\
\end{array}
\]