Açı Ölçü Birimleri
Açı Ölçme
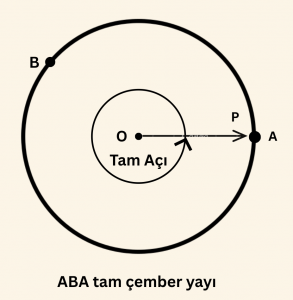
Bir açıyı ölçmek, açının kolları arasındaki açıklığı belirlemektir. Bir çember üzerindeki hareketli bir \(P\) noktası, \(A\) noktasından başlayarak pozitif yönde bir tam dönüş yaparak tekrar \(A\) noktasına gelsin.
\(\widehat{ABA}\) tam çember yayını gören merkez açıya tam açı denir.
1) Derece
Tam çember yayını 360 eş parçaya bölelim. Bu parçalardan her birini gören merkez açının ölçüsü 1 derece olarak tanımlanır.
Dolayısıyla tam açının ölçüsü:
\[
360^\circ
\]
Ayrıca:
\[
1^\circ = 60^{‘} \quad \text{(dakika)} \quad\quad
1^{‘} = 60^{” }\quad \text{(saniye)}
\]
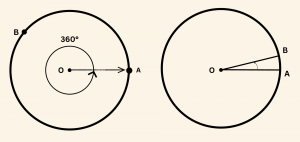
\[
\frac{|\overset{\frown}{ABA}|}{360^\circ} =\overset{\frown}{AB}
= m(\widehat{AOB}) = 1^\circ
\]
2) Grad
Tam çember yayını 400 eş yay parçasına bölelim. Bu parçalardan herbirini gören merkez açının ölçüsü 1 grad olarak tanımlanır. O halde tam açının ölçüsü 400 graddır.

\[
\frac{|\overset{\frown}{ABA}|}{400} =\overset{\frown}{AB}
= m(\widehat{AOB}) = 1 \;\; \text{grad }
\]
3) Radyan
Yarıçap uzunluğuna eşit uzunlukta bir yayı gören merkez açının ölçüsü 1 radyan olarak tanımlanır. Bu tanıma göre, tam bir çemberin çevresi \(2\pi r\) olduğuna göre, bir tam açı şu şekilde hesaplanır:
\[
\frac{2\pi r}{r} = 2\pi \text{ radyandır.} \]
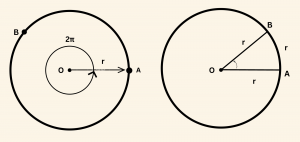
\[ | \overset{\frown}{AB} | = r, \quad |OA |= r , \quad m(\overset{\frown}{AOB} )= 1 \;\; \text{radyan }\]
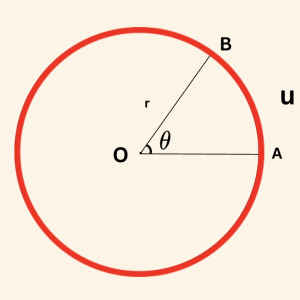
Bir çemberde, bir yay parçasının uzunluğu,
\[
u = |\theta| \cdot r \quad \text{dir.}
\]
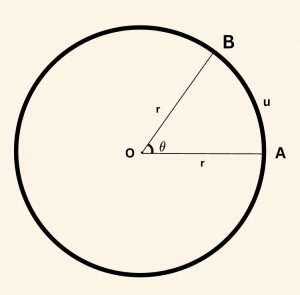
Örnek

Yukarıdaki şekilde \( O \) merkezli çemberin yarıçapı \( r = 24 \, \text{cm} \), \( |\overset{\frown}{AB}| = 25,12 \, \text{cm} \)
olduğuna göre, \( m(\widehat{AOB}) = \theta \) açısının yaklaşık değerini bulalım. (\( \pi \approx 3{,}14 \))
\[
u = |\theta| \cdot r \Rightarrow 25{,}12 = x \cdot 24
\quad \Rightarrow \quad
x = \frac{25{,}12}{24} \text{ radyan olur.}
\]
Bu değeri \(\pi\) cinsinden ifade etmek için:
\[
\begin{aligned}
&3,14 \quad \quad &\pi \\
\\
&\frac{25,12}{24} \quad \quad & |\theta| \\
\hline
\\
&\text{Doğru orantı olduğundan, }
\end{aligned}
\]
\[ \frac{25,12}{24} \cdot \frac{\pi}{3,14} = |\theta| \]
\[
\Rightarrow |\theta| = \frac{\pi}{3} \text{ radyan bulunur.}
\]
Örnek:
Bir çemberde, yarıçap uzunluğunun \( 0,785 \) katı uzunluktaki yayı gören merkez açının ölçüsünün kaç radyan olduğunu bulalım.
\( u = 0,785\, r \) ise,
\( u = |\theta| \cdot r \)
\( \Rightarrow 0,785 \cdot r = x \cdot r \)
\( \Rightarrow x = 0,785 \) radyan olur.
O halde,
\[
\begin{aligned}
&3,14 \quad &\pi \\
\\
&0,785 \quad & |\theta| \\
\hline
\\
&\text{Doğru orantı olduğundan, }
\end{aligned}
\]
\[ |\theta| = \frac{0,785 \pi }{3,14} = \frac{\pi}{4} \]
Açı Ölçü Birimlerini Birbirine Çevirme:
Bir tam açının ölçüsü için,
\[360° = 400 \;\; \text{grad} = 2\pi \;\; \text{radyan} \]
eşitlikleri olduğundan açı ölçü birimlerini aşağıdaki orantı yardımıyla birbirine çevirebiliriz.
\[
\frac{D}{180} = \frac{R}{\pi} = \frac{G}{200}
\]
Buradan,
\[ 1^\circ = \frac{\pi}{180} \;\; radyan ≐ 0,0174 \;\; radyan \]
\[ 1 radyan = \frac{180^\circ}{\pi} ≐ 57°’dir.\]
Örnek:
50°’lik bir açının, radyan ve grad cinsinden ölçülerini bulalım.
\[
\frac{D}{180} = \frac{R}{\pi} = \frac{G}{200} \Rightarrow \frac{50}{180} = \frac{R}{\pi} = \frac{G}{200}
\]
\[
\Rightarrow R = \frac{50\pi}{180} = \frac{5\pi}{18} \text{ radyan}
\]
\[
\Rightarrow G = \frac{50 \cdot 200}{180}
\Rightarrow G = \frac{500}{9} \text{ grad bulunur.}
\]
Örnek:
\( \frac{11\pi}{2} \) radyanlık bir açının, derece ve grad cinsinden ölçülerini bulalım.
\[
\frac{D}{180} = \frac{R}{\pi} = \frac{G}{200} \Rightarrow \frac{D}{180} = \frac{\frac{11 \pi }{2} }{\pi} = \frac{G}{200}
\]
\[
\Rightarrow D = \frac{180 \cdot 11\pi}{2\pi} = 990^\circ
\]
\[
\Rightarrow G = \frac{11\pi \cdot 200}{2\pi}
\Rightarrow G = 1100 \text{ grad bulunur.}
\]
Uyarı:
Ölçüsü radyan cinsinden verilen bir açının derece cinsinden ölçüsünü bulmak için \( \pi \) yerine 180 yazmak yeterlidir.
Örnek:
\( \bullet\ \frac{7\pi}{5} \) radyan = \( \left( \frac{7 \cdot 180}{5} \right)^\circ = 252^\circ \)
\( \bullet\ 11\pi \) radyan = \( (11 \cdot 180)^\circ = 1980^\circ \) dir.
← Önceki Sayfa | Sonraki Sayfa →