Sarma Fonksiyonu
Sarma fonksiyonu, \(\mathbb{R}\) reel sayılar kümesinden
\(\mathbb{Ç}\) birim çemberin üzerindeki noktalara tanımlanan bir fonksiyondur. Sarma fonksiyonunu \( s \) ile gösterirsek,
\[
s : \mathbb{R} \rightarrow \mathbb{Ç}
\]
Analitik düzlemde, \( x = 1 \) doğrusu birim çembere A(1, 0) noktasında teğettir. Bu doğruyu reel sayı ekseni olarak alalım. Bu sayı ekseninin başlangıç (sıfır) noktası birim çemberin A(1, 0) noktasıyla çakışıktır. Şimdi, reel sayı ekseninin birim çember üzerine sarıldığını düşünelim. Böylece reel sayı doğrusu üzerinde her bir \( t \) sayısı birim çemberin sadece bir \( (x, y) \) noktası ile çakışır. Bu çakışmanın sağladığı \( t \rightarrow (x, y) \) eşleştirmesi \( s \) sarma fonksiyonunun kuralıdır.
Birim çemberin çevresi
\[
\mathbb{Ç} = 2\pi R = 2\pi \cdot 1 = 2\pi \text{ dir.}
\]
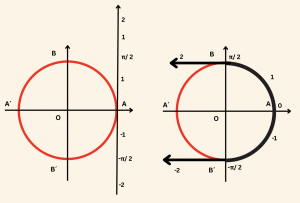
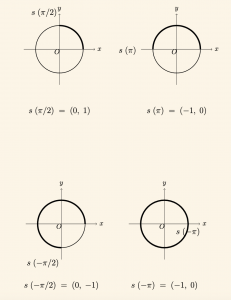
Buna göre \( s \) fonksiyonunun yaptığı eşlemelerden bazıları aşağıda gşsterilmiştir.
Örnek:
\( s \) sarma fonksiyonunu gösterdiğine göre, \( s\left(\frac{\pi}{4}\right) \) görüntüsünü bulalım.
Yandaki şekilden
\( a = b \) ve \( P \) noktası birim çember üzerinde bulunduğundan
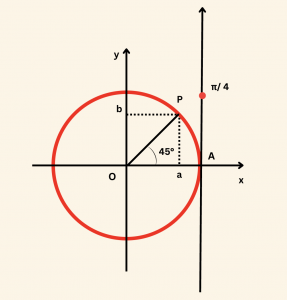
\[
\begin{aligned} a^2 + b^2 = 1 \\
\Rightarrow a^2 + a^2 = 1 \\
\Rightarrow 2a^2 = 1 \\
\Rightarrow a^2 = \frac{1}{2} \\
\Rightarrow a = b = \frac{1}{\sqrt{2}} \quad (\text{a > 0 olduğundan})
\end{aligned}
\]
O halde,
\[
s\left(\frac{\pi}{4}\right) = \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right)
\]
bulunur. Sarma fonksiyonunun kuralı başka şekillerde de verilebilir.
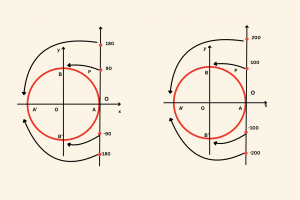
Örneğin,
\( \bullet \quad s'(180) = (-1, 0) \)
\(\bullet \quad s'(-90) = (0, -1) \)
\( \bullet \quad s^{”}(200) = (-1, 0) \)
\( \bullet \quad s^{”}(-100) = (0, -1) \)
Buna göre birim çemberde,
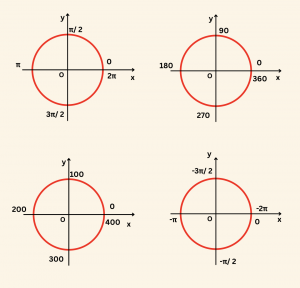
eşlemeleri yapılabilir.
Örneğin,
\( s(\pi) = s'(180) = s^{”}(200) = (-1, 0) \)
Burada şuna dikkat edilmelidir. Reel sayı eksenini, birim çember üzerine sarma işlemi sürdürülecek olursa; sayı ekseni üzerindeki birden fazla nokta birim çember üzerindeki bir nokta ile çakışacaktır.
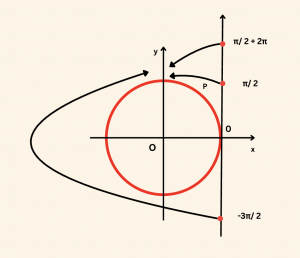
Buna göre,
\( s\left(\frac{\pi}{2}\right) = s\left(\frac{\pi}{2} + 2\pi\right) = s\left(\frac{\pi}{2} – 2\pi\right) = (0, 1) \) dir.
\( k \in \mathbb{Z} \) olmak üzere reel sayı doğrusu üzerindeki bir \( t \) sayısı birim çember üzerindeki bir \( P \) noktası ile çakışıyor ise \( t + 2k\pi \) sayısı da bu \( P \) noktasıyla çakışır.
\( s(t) = s(t + 2k\pi) = P \) yazılabilir.
← Önceki Sayfa | Sonraki Sayfa →