Tanjant Teoremi

 

Tanjant Teoremi

 

 

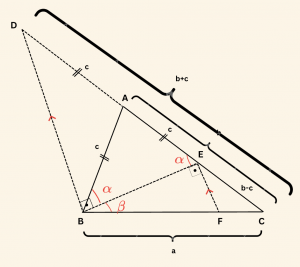
ABC üçgeninde, \( a > b > c \)  olsun.

\[ |AD| = |AB| = |AE| = c \quad   \text{ alalım.} \] Buradan, EBD üçgeni dik olur. Yani, \( m(\hat{ EBD}) = 90^\circ \) olur.

\[ [BD] \parallel [EF] \quad   \text{ çizelim. } \quad   m(\hat{ BEF} ) = 90^\circ \;\; \text{ olur.} \]
\[ m(\hat { ABE}) = m(\hat { AEB}) = \alpha \;\; \text{ ve } \;\; m(\hat{ EBC}) = \beta \;\; \text{ olsun.} \]

\[ \text{BEC üçgeninde }\;\;  \alpha = \beta + C \;\; \text{ ve }\;\;  \alpha\; -\;  \beta = C \;\; \text{ olur.} \]
\[\alpha + \beta = B  \;\;  \text{ olup } \;\;  \alpha = \frac{B + C}{2} \;\;  \text{ ve } \;\;  \beta = \frac{B – C}{2}\;\;  \text{ bulunur.} \]

DBE dik üçgeninde,
\[ \tan \left( \frac{B + C}{2} \right) = \frac{|BD|}{|BE|} \]

BEF dik üçgeninde,
\[ \tan \left( \frac{B – C}{2} \right) = \frac{|EF|}{|BE|} \]

Elde edilen iki eşitliği taraf tarafa bölelim.

\[
\frac{\tan \left( \frac{B + C}{2} \right)}{\tan \left( \frac{B\; -\; C}{2} \right)} = \frac{|BD|}{|EF|} \text{ olur.}
\]

\(  \triangle DBC \sim \triangle EFC \) olduğundan

\[
\frac{|BD|}{|EF|} = \frac{|CD|}{|CE|} \text{ dir.}
\]

 

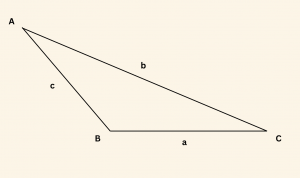
O halde,

\[
\frac{\tan \left( \frac{B + C}{2} \right)}{\tan \left( \frac{B – C}{2} \right)} = \frac{b + c}{b – c} \text{ dır.}
\]

Örnek:

 

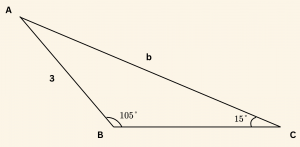
Yandaki şekilde verilenlere göre, \( |AC| = b \) uzunluğunu bulalım.

 

 

 

\[
\frac{B + C}{2} = \frac{105^\circ + 15^\circ}{2} = 60^\circ
\]

\[
\frac{B – C}{2} = \frac{105^\circ – 15^\circ}{2} = 45^\circ
\]

ABC üçgeninde tanjant teoremi yazılırsa,

\[\begin{aligned}& \frac{\tan \left( \frac{B + C}{2} \right)}{\tan \left( \frac{B – C}{2} \right)} = \frac{b + c}{b – c}
\Rightarrow \frac{\tan 60^\circ}{\tan 45^\circ} = \frac{b + 3}{b – 3} \end{aligned}\]

\[\begin{aligned}\Rightarrow \frac{\sqrt{3}}{1} = \frac{b + 3}{b – 3} \\ \\
\Rightarrow \sqrt{3} \cdot (b – 3) = b + 3 \\ \\
\Rightarrow \sqrt{3} b – 3 \sqrt{3} = b + 3 \\ \\
\Rightarrow \sqrt{3} b – b = 3 + 3 \sqrt{3} \\ \\
\Rightarrow b(\sqrt{3} – 1) = 3(1 + \sqrt{3}) \end{aligned}\]

\[
\Rightarrow b = 6 + 3 \sqrt{3} \text{ birimdir.}
\]