Trigonometrik Fonksiyonlar
1) Kosinus ve Sinus Fonksiyonları:
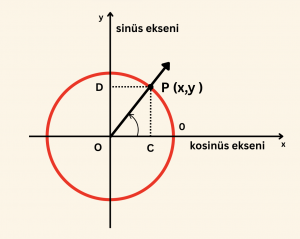
\( \alpha \) açısının bitim kenarının (OP) birim çemberi kestiği P noktasının apsisine \( \alpha \) nın kosinüsü denir ve “\( \cos \alpha \)” şeklinde gösterilir.
P noktasının ordinatına da \( \alpha \) nın sinüsü denir ve \( \sin \alpha \) şeklinde gösterilir.
Buna göre,
\[
\begin{aligned}
\cos \alpha &= |OC| = x \\
\sin \alpha &= |OD| = y
\end{aligned}
\]
Birim çemberde Ox eksenine kosinüs ekseni, Oy eksenine de sinüs ekseni denir.
Örnek:
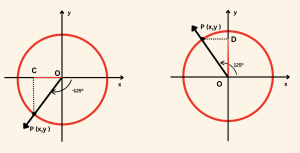
\( \cos(-125^\circ) \) ve \( \sin125^\circ \) değerlerini birim çember çizerek gösterelim.
← Önceki Sayfa | Sonraki Sayfa →
\[
\cos(-125^\circ) = -|OC| < 0 \]
\[\sin(125^\circ) = |OD| > 0
\]
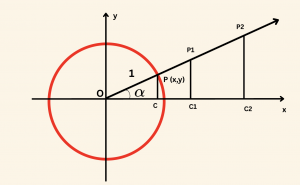
Şimdi de dar açıların kosinüslerini ve sinüslerini bulalım.
Burada,
\[
\triangle OPC \sim \triangle OP_1C_1 \sim \triangle OP_2C_2 \sim \ldots \text{ dir.}
\]
O halde,
\[
\cos \alpha = x = \frac{|OC|}{1} = \frac{|OC|}{|OP|} = \frac{|OC_1|}{|OP_1|} = \frac{|OC_2|}{|OP_2|} = \ldots \text{ dir.}
\]
Buna göre bir dik üçgende,
\[
\cos \alpha = \frac{\text{komşu dik kenarın uzunluğu}}{\text{hipotenüsün uzunluğu}} \text{ olur.}
\]
Benzer şekilde,
\[
\sin \alpha = y = \frac{|CP|}{1} = \frac{|CP|}{|OP|} = \frac{|C_1P_1|}{|OP_1|} = \frac{|C_2P_2|}{|OP_2|} = \ldots \text{ dir.}
\]
Buna göre bir dik üçgende,
\[
\sin \alpha = \frac{\text{karşı dik kenarın uzunluğu}}{\text{hipotenüsün uzunluğu}} \text{ olur.}
\]
2) Tanjant ve Kotanjant Fonksiyonları:
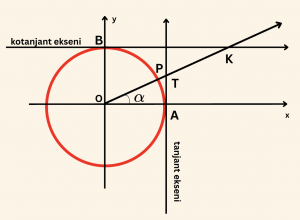
\( \alpha \) açısının bitim kenarı ([OP]), birim çembere A noktasından çizilen teğeti, T noktasında; B noktasından çizilen teğeti K noktasında kessin.
T noktasının ordinatına \( \alpha \) nın tanjantı denir ve \( \tan \alpha \) şeklinde gösterilir.
K noktasının apsisine de \( \alpha \) nın kotanjantı denir ve \( \cot \alpha \) şeklinde gösterilir.
Buna göre,
\[
\begin{aligned}
\tan \alpha &= \frac{\sin \alpha}{\cos \alpha} = |AT| \\ \\ \cot \alpha &= \frac{\cos \alpha}{\sin \alpha} = |BK|
\end{aligned}
\]
Birim çembere A(1, 0) noktasından çizilen teğete tanjant ekseni, B(0, 1) noktasından çizilen teğete de kotanjant ekseni denir.
Örnek:
\( \tan40°, \;\; \tan230°, \;\; \) ve \( \cot330° \) değerlerini birim çember çizerek gösterelim.
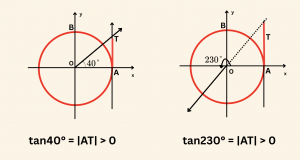
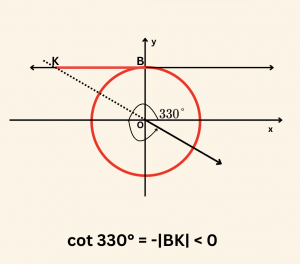
Şimdi de dar açıların tanjantlarını ve kotanjantlarını bulalım.
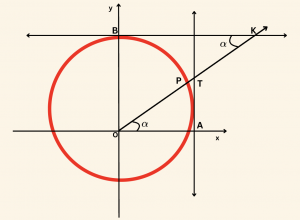
Burada,
\[
\tan \alpha = |AT| = \frac{|AT|}{1} = \frac{|AT|}{|OA|} \text{ dır.}
\]
Buna göre bir dik üçgende,
\[
\tan \alpha = \frac{\text{karşı dik kenarın uzunluğu}}{\text{komşu dik kenarın uzunluğu}}
\]
Benzer şekilde,
\[
\cot \alpha = |BK| = \frac{|BK|}{1} = \frac{|BK|}{|OB|} \text{ dir.}
\]
Buna göre bir dik üçgende,
\[
\cot \alpha = \frac{\text{komşu dik kenarın uzunluğu}}{\text{karşı dik kenarın uzunluğu}}
\]
3) Sekant ve Kosekant Fonksiyonları:
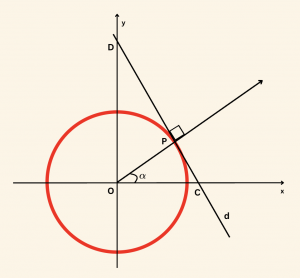
\( \alpha \) açısının bitim kenarının ([OP]) birim çemberi kestiği P noktasında, \( d \) doğrusu birim çembere teğettir.
C noktasının apsisine \( \alpha \) nın sekantı denir ve \( \sec \alpha \) şeklinde gösterilir.
D noktasının ordinatına da \( \alpha \) nın kosekantı denir ve \( \csc \alpha \) şeklinde gösterilir.
Buna göre,
\[
\begin{aligned}
\sec \alpha &= \frac{1}{\cos \alpha} = |OC| \\
\csc \alpha &= \frac{1}{\sin \alpha} = |OD|
\end{aligned}
\]