Trigonometrik Fonksiyonların Özellikleri
1)

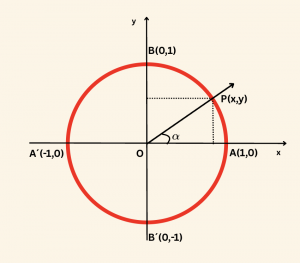
Birim çemberin denklemi \( x^2 + y^2 = 1 \), \( \quad x = \cos \alpha \quad \) ve \( \quad y = \sin \alpha \quad \) olduğundan,
\[
\cos^2 \alpha + \sin^2 \alpha = 1
\]
dir.
2)
\[ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} \quad \] ve \[ \cot \alpha = \frac{\cos \alpha}{\sin \alpha} \] olduğundan,
\[
\tan \alpha \cdot \cot \alpha = 1
\]
3)
\[
1 + \tan^2 \alpha = 1 + \frac{\sin^2 \alpha}{\cos^2 \alpha} = \frac{\cos^2 \alpha + \sin^2 \alpha}{\cos^2 \alpha}
= \frac{1}{\cos^2 \alpha} = \sec^2 \alpha
\]
\[
\Rightarrow 1 + \tan^2 \alpha = \sec^2 \alpha
\]
\[
1 + \cot^2 \alpha = 1 + \frac{\cos^2 \alpha}{\sin^2 \alpha} = \frac{\cos^2 \alpha + \sin^2 \alpha}{\sin^2 \alpha}
= \frac{1}{\sin^2 \alpha} = \csc^2 \alpha
\]
\[
\Rightarrow 1 + \cot^2 \alpha = \csc^2 \alpha
\]
4)
\[
\cos \alpha = x \Rightarrow -1 \leq x \leq 1, \quad \cos : \mathbb{R} \to [-1, 1]
\]
\[
\sin \alpha = y \Rightarrow -1 \leq y \leq 1, \quad \sin : \mathbb{R} \to [-1, 1]
\]
O halde, sinüs ve kosinüs fonksiyonlarının alacağı en küçük değer \(-1\), en büyük değer \(1\) dir.
\[-1 \leq \cos \alpha \leq 1 \]
\[ -1 \leq \sin \alpha \leq 1\]
5)
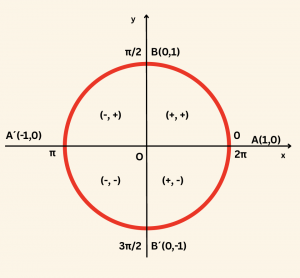
Ox ekseni kosinüs ekseni ve Oy ekseni de sinüs ekseni olduğundan bir \( \alpha \) açısının herhangi bir trigonometrik oranın işaretini bulmak için bu açının bitim kenarının birim çemberi kestiği noktanın koordinatlarının işaretine bakılır. Bu noktanın apsisinin işareti \( \cos \alpha \)’nın, ordinatının işareti ise \( \sin \alpha \)’nın işaretidir.
\[
\begin{array}{|c|c|c|c|c|}
\hline
& \textbf{1. Bölge} & \textbf{2. Bölge} & \textbf{3. Bölge} & \textbf{4. Bölge} \\
& 0 < \alpha < \frac{\pi}{2} & \frac{\pi}{2} < \alpha < \pi & \pi < \alpha < \frac{3\pi}{2} & \frac{3\pi}{2} < \alpha < 2\pi \\
\hline
\cos \alpha & + & – & – & + \\
\hline
\sin \alpha & + & + & – & – \\
\hline
\tan \alpha & + & – & + & – \\
\hline
\cot \alpha & + & – & + & – \\
\hline
\end{array}
\]
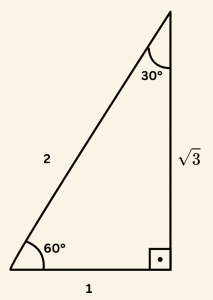
6) \( 30^\circ, 45^\circ \) ve \( 60^\circ \)’lik açıların trigonometrik oranları:
\[
\sin 30^\circ = \cos 60^\circ = \frac{1}{2}
\]
\[
\cos 30^\circ = \sin 60^\circ = \frac{\sqrt{3}}{2}
\]
\[
\tan 30^\circ = \cot 60^\circ = \frac{1}{\sqrt{3}}
\]\[
\cot 30^\circ = \tan 60^\circ = \sqrt{3}
\]
\[
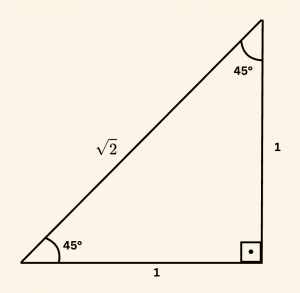
\sin 45^\circ = \cos 45^\circ = \frac{1}{\sqrt{2}}
\]
\[
\tan 45^\circ = \cot 45^\circ = 1 \quad \text{ olarak bulunur.}
\]
7) \(0^\circ, 90^\circ, 180^\circ\) ve \(270^\circ\)’lik açıların trigonometrik oranları:
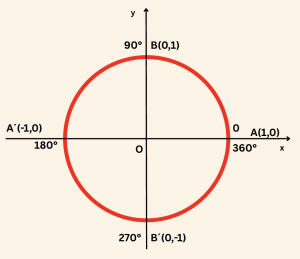
Bir \( \alpha \) açısının bitim kenarının birim çemberi kestiği noktanın apsisi \( \cos \alpha \), ordinatı da \( \sin \alpha \) olduğundan;
yukarıdaki birim çemberde A, B, A’, B’ noktaları kullanılarak trigonometrik oranlar:
\[
\begin{array}{|c|c|c|c|c|}
\hline
\alpha & 0^\circ\ (360^\circ) & 90^\circ & 180^\circ & 270^\circ \\
\hline
\sin \alpha & 0 & 1 & 0 & -1 \\
\hline
\cos \alpha & 1 & 0 & -1 & 0 \\
\hline
\tan \alpha & 0 & \text{tanımsız} & 0 & \text{tanımsız} \\
\hline
\cot \alpha & \text{tanımsız} & 0 & \text{tanımsız} & 0 \\
\hline
\end{array}
\]
8)
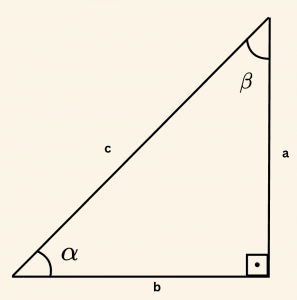
\[
\alpha + \beta = 90^\circ = \frac{\pi}{2} \text{ radyan}
\]
\[\sin \alpha = \frac{a}{c} = \cos \beta \]
\[\tan \alpha = \frac{a}{b} = \cot \beta \]
\[\sec \alpha = \frac{c}{b} = \csc \beta \]
Tümler iki açıdan birinin sinüsü, diğerinin kosinüsüne; birinin tanjantı, diğerinin kotanjantına; birinin sekantı, diğerinin kosekantına eşittir.
Örnekler:
\( \bullet \quad \sin(90^\circ – \; \theta) = \cos \theta \)
\( \bullet \quad \tan(30^\circ + x -\; y) = \cot(60^\circ -\; x + y) \)
\( \bullet \quad \sec \frac{2\pi}{5} = \csc \frac{\pi}{10} \quad \to \left( \frac{2\pi}{5} + \frac{\pi}{10} = \frac{\pi}{2} \right) \)
SORU 1
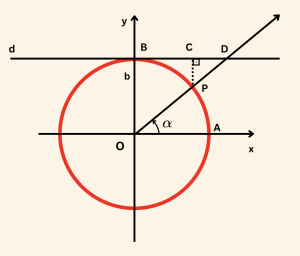
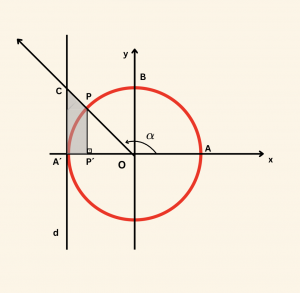
Yandaki şekilde \( d \) doğrusu birim çembere B noktasında teğettir. \( m(\widehat{AOP}) = \alpha \) olduğuna göre
\( |CD| \) aşağıdakilerden hangisine eşittir?
\[
\text{A) } 1\; – \; \tan \alpha \quad
\text{B) } \cot \alpha \;- \;1 \quad
\text{C) } \tan \alpha\; -\; \sin \alpha \quad
\text{D) } \cot \alpha \;-\; \sin \alpha \quad
\text{E) } \cot \alpha \;- \;\cos \alpha
\]
Çözüm:
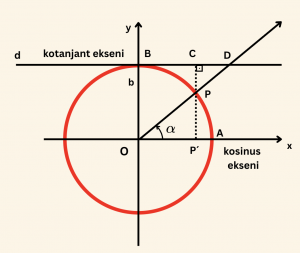
P noktasının apsisi \( \cos \alpha \) olduğundan
\[
|OP´| = |BC| = \cos \alpha
\]
D noktasının apsisi \( \cot \alpha \) olduğundan
\[
|BD| = \cot \alpha
\]
O halde,
\[
|CD| = |BD| – |BC| = \cot \alpha \; -\; \cos \alpha
\]
\(\textbf{Cevab: E} \)
SORU 2
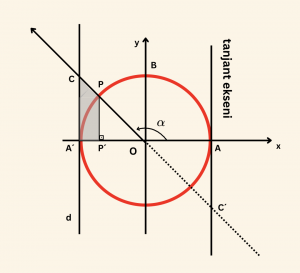
Yandaki şekilde d doğrusu birim çembere A’ noktasında teğettir. \( m(A\hat{O}P) = \alpha \) olduğuna göre, A’P’PC yamuğunun alanı aşağıdakilerden hangisine eşittir?
\[
\text{A) } -\frac{\sin^3 \alpha}{2 \cos \alpha }\quad
\text{B) } \frac{1}{2} (1 + \sin^2 \alpha) \quad
\text{C) } \frac{1}{2} \tan \alpha \sin \alpha \quad
\text{D) } -\frac{1}{2} (1 + \cos \alpha) \tan \alpha \quad
\text{E) } \frac{1}{2} \tan \alpha
\]
Çözüm:
 C’ noktasının ordinatı \( \tan \alpha \) olduğundan
C’ noktasının ordinatı \( \tan \alpha \) olduğundan
\( |AC’| = |A’C| = -\tan \alpha \)
P noktasının apsisi \( \cos \alpha \) ve ordinatı \( \sin \alpha \) olduğundan
\( |OP’| = -\cos \alpha \) ve \( |A’P’| = 1 \; – \; (\;-\cos \alpha) = 1 + \cos \alpha \)
\( |PP’| = \sin \alpha \) dır.
O halde,
\[A(A’P’PC) = \frac{(|A’C| + |PP’|) \cdot |A’P’|}{2} \]
\[ = \frac{(-\tan \alpha + \sin \alpha)(1 + \cos \alpha)}{2} \]
\[ = -\frac{\sin^3 \alpha}{2 \cos \alpha} \;\; dır. \]
\(\textbf{Cevab: A} \)
SORU 3
\( a = \cos 70^\circ, \quad b = \cos 200^\circ, \quad c = \sin 200^\circ \) ve \( d = \cos 285^\circ \) değerlerinin büyükten küçüğe doğru sıralanışı aşağıdakilerden hangisidir?
\[\begin{aligned}
&\text{A) } a > b > c > d \quad \\
&\text{B) } a > d > c > b \quad \\
&\text{C) } d > a > c > b \quad \\
&\text{D) } d > c > a > b \quad \\
&\text{E) } b > c > a > d
\end{aligned}
\]
Çözüm:
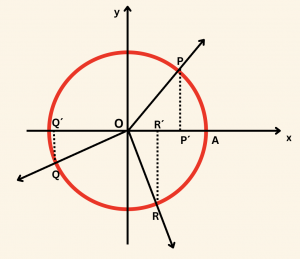 Yandaki şekilde \( m( A\hat{O}P ) = 70^\circ \) ve P noktasının apsisi \( a = \cos 70^\circ = |OP’| \)
Yandaki şekilde \( m( A\hat{O}P ) = 70^\circ \) ve P noktasının apsisi \( a = \cos 70^\circ = |OP’| \)
\( m( A\hat{O}Q) = 200^\circ \) ve
Q noktasının apsisi \( b = \cos 200^\circ = -|OQ’| \) ordinatı \( c = \sin 200^\circ = -|QQ’| \)
\( m(A\hat{O}R) = 285^\circ \) ve R noktasının apsisi \( d = \cos 285^\circ = |OR’| \) dir.
Burada, \( m(Q\hat{O}Q’) < m(O\hat{Q}Q’) \) olduğundan
\( |QQ’| < |OQ’| \) olup \( c = -|QQ’| > b = -|OQ’| \) olur.
O halde,
\( |OP’| > |OR’| > -|QQ’| > -|OQ’| \) olduğundan, \( a > d > c > b \) dir.
\(\textbf{Cevab: B} \)
SORU 4
\( a = \tan 40^\circ, \quad b = \cos 55^\circ \) ve \(c = \sin 40^\circ \) değerlerinin büyükten küçüğe doğru sıralanışı aşağıdakilerden hangisidir?} \\
\[\begin{aligned}
&\text{A) } c > a > b \quad \\
&\text{B) } b > a > c \quad \\
&\text{C) } a > c > b \quad \\
&\text{D) } a > b > c \quad \\
&\text{E) } b > c > a
\end{aligned}
\]
Çözüm:
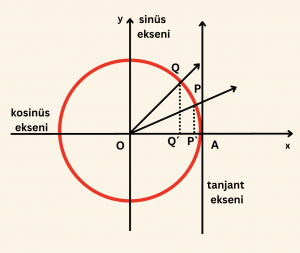
Yandaki şekilde, \( m( A\hat{O}T) = 40^\circ \) olduğundan T noktasının ordinatı
\[a = \tan 40^\circ = |AT| \]
\( m(A\hat{O}P) = 35^\circ \) olduğundan P noktasının ordinatı \( b = \cos 55^\circ = \sin 35^\circ = |PP’| \)
\[ m(A\hat{O}Q) = 40^\circ \]
ve Q noktasının ordinatı
\[c = \sin 40^\circ = |QQ’| \text{ dir.} \]
O halde,
\[ |AT| > |QQ’| > |PP’| \text{ olduğundan } a > c > b \text{ olur.} \]
\(\textbf{Cevab: C} \)
SORU 5
\[ \frac{\sin x + \cot x \cdot \cos x}{\cos x + \tan x \cdot \sin x} \] işleminin sonucu aşağıdakilerden hangisidir?
\[\begin{aligned}
\text{A) } \cos x \quad
\text{B) } \sin x \quad
\text{C) } 1 \quad
\text{D) } \cot x \quad
\text{E) } \tan x \\
\end{aligned}
\]
Çözüm:
\[ = \frac{\sin x + \cot x \cdot \cos x}{\cos x + \tan x \cdot \sin x } \]
\[ = \frac{\sin x + \frac{\cos x}{\sin x} \cdot \cos x}{\cos x + \frac{\sin x}{\cos x} \cdot \sin x} \]
=\frac{\frac{\sin^2 x + \cos^2 x}{\sin x}}{\frac{\cos^2 x + \sin^2 x}{\cos x}}
\]
\[ = \frac{\cos x}{\sin x} = \cot x \, \text{tir}. \]
\(\textbf{Cevab: D} \)
SORU 6
\[ x = \cos \theta \quad \text{ve} \quad y = \sin \theta \] ise \[ x^4 – y^4 + 2x^2 – y^2 + 2 \] ifadesi aşağıdakilerden hangisine eşittir?
\[\begin{aligned}
\text{A) }5\cos^2 \theta \quad
\text{B) } 4\cos^2 \theta \quad
\text{C) } 3\cos^2 \theta \quad
\text{D) } 2\cos^2 \theta \quad
\text{E) }\cos^2 \theta \\
\end{aligned}
\]
Çözüm:
\[x^4 – y^4 + 2x^2 – y^2 + 2 = (x^2 + y^2)(x^2 – y^2) + 2x^2 – y^2 + 2 \]
\[ \cos^2 \theta + \sin^2\theta = 1 \Rightarrow x^2 + y^2 = 1 \quad \text{olduğundan} \]
\[\Rightarrow 3x^2-2y^2+2 \]
\[=3x^2+2( 1 – y^2) \] ve
\[ =3x^2+ 2x^2 \]
\[ = 5x^2= 5 \cos^2\theta \]
\(\textbf{Cevab: A} \)
SORU 7
\[
\frac{7 + 5 \sin^2 x – \cos^2 x}{3 \sin^2 x + 2 \cos^2 x – 1}
\]
kesirinin sadeleştirilmiş şekli nedir?
\[
\text{A) } 4 \quad
\text{B) } 5 \quad
\text{C) } 6 \quad
\text{D) } 7 \quad
\text{E) } 8
\]
Çözüm:
\[
\frac{7 + 5 \sin^2 x – \cos^2 x}{3 \sin^2 x + 2 \cos^2 x – 1}
= \frac{6 + 5 \sin^2 x + 1 – \cos^2 x}{\sin^2 x + 2(\sin^2 x + \cos^2 x) – 1}
\]
\[
= \frac{6 + 5 \sin^2 x + \sin^2 x}{\sin^2 x + 2 \cdot 1 – 1}
= \frac{6 + 6 \sin^2 x}{\sin^2 x + 1}
\]
\[
= \frac{6(\sin^2 x + 1)}{\sin^2 x + 1} = 6
\]
\(\textbf{Cevab: C} \)
SORU 8
\(\frac{\pi}{2} < \theta < \pi\) olmak üzere ve \(x = \cos \theta\), \(y = \sin \theta\) ise
\[
\frac{\sqrt{1 – 2xy}}{x^3 – x^2 y + xy^2 – y^3}
\]
olduğuna göre kesirin sadeleştirilmiş şekli nedir?
\[
\text{A) } -2 \quad
\text{B) } -1 \quad
\text{C) } 0 \quad
\text{D) } 1 \quad
\text{E) } 2
\]
Çözüm:
\[
\frac{\sqrt{1 – 2xy}}{x^3 – x^2 y + xy^2 – y^3}
= \frac{\sqrt{1 – 2xy}}{(x – y)(x^2 + y^2)}
\]
\[
\cos^2 \theta + \sin^2 \theta = 1 \Rightarrow x^2 + y^2 = 1 \quad \text{olduğundan }
\]
\[
= \frac{\sqrt{x^2 + y^2 – 2xy}}{(x – y ) \cdot 1 }
= \frac{|\ x – y\ |}{x – y}
\]
\(\frac{\pi}{2} < \theta < \pi \Rightarrow \cos \theta < 0\), \(\sin \theta > 0 \)
\[ \Rightarrow x – y < 0\]
\[
= \frac{-(x – y)}{x – y} = -1
\]
\(\textbf{Cevab: B} \)
SORU 9
\[
\frac{\sin^2 x}{\cos x – \sec x} + \frac{\cos^2 x}{\sin x – \csc x}
\]
ifadesinin eşiti aşağıdakilerden hangisidir?
\[
\text{A) } 1 \quad
\text{B) } \sin x + \cos x \quad
\text{C) } \cos x – \sin x \quad
\text{D) } \sin x – \cos x \quad
\text{E) } -\cos x – \sin x
\]
Çözüm:
\[
\frac{\sin^2 x}{\cos x – \sec x} + \frac{\cos^2 x}{\sin x – \csc x}
\]
\[
= \frac{\sin^2 x}{\cos x – \frac{1}{\cos x}} + \frac{\cos^2 x}{\sin x – \frac{1}{\sin x}}
\]
\[
= \frac{\sin^2 x \cdot \cos x}{\cos^2 x – 1} + \frac{\cos^2 x \cdot \sin x}{\sin^2 x – 1}
\]
\[
= \frac{\sin^2 x \cdot \cos x}{- \sin^2 x} + \frac{\cos^2 x \cdot \sin x}{- \cos^2 x}
\]
\[
= -\cos x – \sin x
\]
\(\textbf{Cevab: E} \)
SORU 10
\[
\frac{3\pi}{2} < x < 2\pi \text{ olmak üzere,}
\]
\[
\sqrt{\frac{1 – \cos x}{1 + \cos x}} + \sqrt{\frac{1 + \cos x}{1 – \cos x}}
\]
ifadesinin eşiti aşağıdakilerden hangisidir?
\[
\text{A) } -2 \csc x \quad
\text{B) } 2 \csc x \quad
\text{C) } \sec x\ \quad
\text{D) } -\sec x \quad
\text{E) } 2 \sec x
\]
Çözüm:
\[
\sqrt{\frac{1 – \cos x}{1 + \cos x}} + \sqrt{\frac{1 + \cos x}{1 – \cos x}}
\]
\[
= \sqrt{\frac{(1 – \cos x)^2}{(1 + \cos x)(1 – \cos x)}} + \sqrt{\frac{(1 + \cos x)^2}{(1 – \cos x)(1 + \cos x)}}
\]
\[
= \frac{|1 – \cos x|}{|\sin x|} + \frac{|1 + \cos x|}{|\sin x|}
\]
Verilen aralık: \[\frac{3\pi}{2} < x < 2\pi\]
\[ \Rightarrow 0 < \cos x < 1 \;\; ve \;\; \sin x < 0 \]
\[
\Rightarrow |1 – \cos x| = 1 – \cos x, \quad |1 + \cos x| = 1 + \cos x, \quad |\sin x| = -\sin x
\]
\[
= \frac{1 – \cos x + 1 + \cos x}{-\sin x} = \frac{2}{-\sin x} = -2 \csc x
\]
\(\textbf{Cevab: A} \)
SORU 11
\[
\frac{\pi}{2} < x < \pi \text{ olmak üzere,}
\]
\[
\tan^2 x + \cot^2 x + 2\tan x + 2\cot x – 1 = 0
\]
ise, \(\tan^2 x + \cot^2 x\) toplamının değeri kaçtır?
\[
\text{A) } 3 \quad
\text{B) } 4 \quad
\text{C) } 5 \quad
\text{D) } 6 \quad
\text{E) } 7
\]
Çözüm:
\[
\tan^2 x + \cot^2 x + 2\tan x + 2\cot x – 1 = 0
\]
\[
\Rightarrow (\tan x + \cot x)^2 – 2\; \underbrace{\tan x \cdot \cot x}_{1} + 2(\tan x + \cot x) \;- \;1 = 0
\]
\[
\Rightarrow (\tan x + \cot x)^2 + 2(\tan x + \cot x) – 3 = 0
\]
\[
\text{Tüm ifade için } t = \tan x + \cot x \text{ denilirse:}
\]
\[
t^2 + 2t – 3 = 0 \Rightarrow t = -3 \text{ veya } t = 1
\]
Verilen aralıkta: \( \to \tan x < 0\), \(\cot x < 0 \Rightarrow \tan x + \cot x < 0\),
Dolayısıyla \(t = \tan x + \cot x = -3\) olur, Eşitliğin her iki yanının karesini alalım.
\[
(\tan x + \cot x)^2 = 9
\]
\[
\tan^2 x + \cot^2 x + 2 \cdot \tan x \cdot \cot x = 9
\]
\[
\tan^2 x + \cot^2 x + 2 = 9 \Rightarrow \tan^2 x + \cot^2 x = 7
\]
\(\textbf{Cevab: E} \)
SORU 12
\(x \in (180^\circ,\ 270^\circ)\) olmak üzere,
\[
2 \tan x \; – \; 3 \cot x = 5
\]
ise, \(\tan x\) kaça eşittir?
\[
\text{A) } 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[
\cot x = \frac{1}{\tan x} \text{ olduğundan,}
\]
\[
2 \tan x\; -\; 3 \cdot \frac{1}{\tan x} = 5
\]
\[
\Rightarrow 2 \tan^2 x \;- \; 5 \tan x \;-\; 3 = 0
\]
İkinci dereceden denklemi çözelim
\[
\tan x = t \;\; \text{ denirse, denklem:} \;\; 2t^2\; – \;5t \;-\; 3 = 0
\]
\[
t = \frac{5 \pm \sqrt{(-5)^2 + 4 \cdot 2 \cdot 3}}{2 \cdot 2}
= \frac{5 \pm \sqrt{25 + 24}}{4}
= \frac{5 \pm \sqrt{49}}{4}
= \frac{5 \pm 7}{4}
\]
\[
t = 3 \;\; \text{ veya } \;\; t = -\frac{1}{2}
\]
Verilen aralık: \(x \in (180^\circ, 270^\circ) \Rightarrow \tan x > 0\)
\[
\Rightarrow \tan x = 3
\]
\(\textbf{Cevab: C} \)
SORU 13
\[
f(x) = \frac{-4 \cos x + 1}{3}
\]
fonksiyonunun en büyük değeri \(m\), en küçük değeri \(n\) ise \(m + n\) kaçtır?
\[
\text{A) } 3 \quad
\text{B) } 2 \quad
\text{C) } 1 \quad
\text{D) } \frac{2}{3} \quad
\text{E) } \frac{1}{3}
\]
Çözüm:
\[
-1 \leq \cos x \leq 1 \Rightarrow -4 \cdot (-1) \geq -4 \cos x \geq -4 \cdot 1\]
\[\Rightarrow 4 \geq -4 \cos x \geq -4
\]
\[
1 + 4 \geq -4 \cos x + 1 \geq 1 – 4\] \[ \Rightarrow 5 \geq -4 \cos x + 1 \geq -3
\]
\[
\Rightarrow \frac{5}{3} \geq f(x) \geq \frac{-3}{3}
\Rightarrow -1 \leq f(x) \leq \frac{5}{3}
\]
\[
m = \frac{5}{3}, \quad n = -1 \Rightarrow m + n = \frac{5}{3} – 1 = \frac{2}{3}
\]
\(\textbf{Cevab: D} \)
SORU 14
\[
\frac{ |1 + \cos x| – |1 – \sin x| }{ | \cos x – 1| – \; \sin x – 1 }
\]
kesirinin sadeleştirilmiş şekli aşağıdakilerden hangisidir?
\[
\text{A) } \cot x \quad
\text{B) } \tan x \quad
\text{C) } 1 \quad
\text{D) } 0 \quad
\text{E) } -1
\]
Çözüm:
\[
-1 \leq \cos x \leq 1 \Rightarrow 0 \leq 1 + \cos x \leq 2 \Rightarrow |1 + \cos x| = 1 + \cos x
\]
\[
-1 \leq \cos x \leq 1 \Rightarrow -2 \leq \cos x – 1 \leq 0 \Rightarrow | \cos x – 1 | = -( \cos x – 1 ) = 1 – \cos x
\]
\[
-1 \leq \sin x \leq 1 \Rightarrow 0 \leq 1 – \sin x \leq 2 \Rightarrow |1 – \sin x| = 1 – \sin x
\]
Bu durumda kesir:
\[
\frac{1 + \cos x – (1 – \sin x)}{1 – \cos x – \sin x- 1} = \frac{\cos x + \sin x}{- \cos x – \sin x} = -1
\]
\(\textbf{Cevab: E} \)
SORU 15
\[
\cos 2252^\circ,\quad \tan \frac{169\pi}{8} ,\quad \csc \left(-\frac{57\pi}{7} \right)
\]
trigonometrik değerlerinin işaretleri sırasıyla nedir?
\[
\text{A) } – , – , + \quad
\text{B) } – , – , – \quad
\text{C) } + , – , + \quad
\text{D) } – , + , – \quad
\text{E) } + , – , –
\]
Çözüm:
2252°’nin esas ölçüsünü bulalım:
\[
2252^\circ \mod 360^\circ = 92^\circ
\]
\[
90^\circ < 92^\circ < 180^\circ \Rightarrow \cos 2252^\circ < 0
\]
\[
\frac{169\pi}{8} = 20\pi + \frac{9\pi}{8} \Rightarrow \text{esas ölçü } \frac{9\pi}{8}
\]
\[
\pi < \frac{9\pi}{8} < \frac{3\pi}{2} \Rightarrow \tan \left( \frac{169\pi}{8} \right) > 0
\]
\[
-\frac{57\pi}{7} = -10\pi + \frac{13\pi}{7} \Rightarrow \text{esas ölçü } \frac{13\pi}{7}
\]
\[
\frac{13\pi}{7} \in (\pi, \frac{3\pi}{2}) \Rightarrow \sin \left( -\frac{57\pi}{7} \right) < 0 \Rightarrow \csc \left( -\frac{57\pi}{7} \right) < 0
\]
Sonuç:
\[
\cos: – ,\quad \tan: + ,\quad \csc: –
\]
\(\textbf{Cevab: D} \)
SORU 16
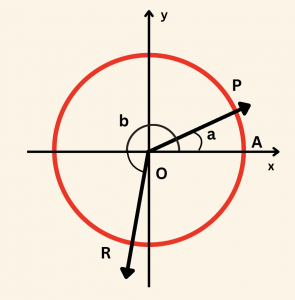
Yandaki birim çemberde
\[
m(\hat{AOP}) = a,\quad m(\hat{AOR}) = b
\]
ise,
\[
\sin(a + b), \quad \tan(\pi + a), \quad \cos\left( \frac{3\pi}{2}\; -\; b \right)
\]
trigonometrik değerlerinin işaretleri sırasıyla nedir?
\[
\text{A) } + , + , + \quad
\text{B) } – , – , – \quad
\text{C) } + , – , – \quad
\text{D) } – , + , – \quad
\text{E) } – , + , +
\]
Çözüm 1:
\[
0 < a < \frac{\pi}{2} \quad ve \quad \pi < b < \frac{3\pi}{2}
\]
\[
\begin{aligned}
0 \lt a \lt \frac{\pi}{2} \\
+ \;\; \; \pi \lt b \lt \frac{3\pi}{2} \\
\hline \\
\pi \lt a+b \lt 2 \pi
\end{aligned}
\]
\[
\Rightarrow \pi < a + b < 2\pi \Rightarrow \sin(a + b) < 0
\]
\[
0 < a < \frac{\pi}{2} \Rightarrow \pi < a + \pi < \frac{3\pi}{2} \Rightarrow \tan(\pi + a) > 0
\]
\[
\pi < b < \frac{3\pi}{2} \Rightarrow -\pi > -b > -\frac{3\pi}{2}
\]
\[
\Rightarrow \frac{3\pi}{2} – \pi > \frac{3\pi}{2} – b > \frac{3\pi}{2} – \frac{3\pi}{2}
\Rightarrow \frac{\pi}{2} > \frac{3\pi}{2} – b > 0
\]
\[
\Rightarrow \cos\left( \frac{3\pi}{2} – b \right) > 0
\]
\[
\sin(a + b) < 0,\quad \tan(\pi + a) > 0,\quad \cos\left( \frac{3\pi}{2} – b \right) > 0
\]
\(\textbf{Cevab: E} \)
Çözüm 2:
a ve b açıları yerine uygun değerler seçilebilir.
\[
a \cong \frac{\pi}{8}, \quad b \cong \frac{11\pi}{8} \text{ olsun.}
\]
\[
a + b = \frac{\pi}{8} + \frac{11\pi}{8} = \frac{12\pi}{8} = \frac{3\pi}{2}
\Rightarrow \sin(a + b) = \sin\left( \frac{3\pi}{2} \right) = -1 < 0
\]
\[
\pi + a = \pi + \frac{\pi}{8} = \frac{9\pi}{8} \Rightarrow \tan\left( \frac{9\pi}{8} \right) > 0
\]
\[
\frac{3\pi}{2} – b = \frac{3\pi}{2} – \frac{11\pi}{8} = \frac{12\pi – 11\pi}{8} = \frac{\pi}{8}
\Rightarrow \cos\left( \frac{3\pi}{2} – b \right) = \cos\left( \frac{\pi}{8} \right) > 0
\]
\[
\sin(a + b) < 0, \quad \tan(\pi + a) > 0, \quad \cos\left( \frac{3\pi}{2} – b \right) > 0
\]
\(\textbf{Cevab: E} \)
SORU 17
\[
\tan\left(\frac{13\pi}{38}\right) \cdot \tan\left(\frac{3\pi}{19}\right)
+ \sin^2\left(\frac{\pi}{9}\right) + \sin^2\left(\frac{7\pi}{18}\right)
\]
işleminin sonucu kaçtır?
\[
\text{A) } 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
\[
\frac{13\pi}{38} + \frac{3\pi}{19}
= \frac{13\pi}{38} + \frac{6\pi}{38}
= \frac{19\pi}{38} = \frac{\pi}{2}
\]
\(\Rightarrow\) açıları tümledir.
\[
\tan\left(\frac{13\pi}{38}\right) = \cot\left(\frac{3\pi}{19}\right)
\]
\[
\frac{\pi}{9} + \frac{7\pi}{18}
= \frac{2\pi}{18} + \frac{7\pi}{18} = \frac{9\pi}{18} = \frac{\pi}{2}
\]
\(\Rightarrow\) açıları tümledir.
\[
\sin\left(\frac{\pi}{9}\right) = \cos\left(\frac{7\pi}{18}\right)
\]
\[
= \cot\left(\frac{3\pi}{19}\right) \cdot \tan\left(\frac{3\pi}{19}\right)
+ \cos^2\left(\frac{7\pi}{18}\right) + \sin^2\left(\frac{7\pi}{18}\right)
\]
\[
= 1 + 1 = 2
\]
\(\textbf{Cevab: B} \)
SORU 18
\[
\cot 5^\circ \cdot \cot 10^\circ \cdot \cot 15^\circ \cdots \cot 80^\circ \cdot \cot 85^\circ
\]
çarpımının sonucu kaçtır?
\[
\text{A) } 5 \quad
\text{B) } 4 \quad
\text{C) } 3 \quad
\text{D) } 2 \quad
\text{E) } 1
\]
Çözüm:
\[
\cot 5^\circ \cdot \cot 10^\circ \cdot \cot 15^\circ \cdots \cot 40^\circ \cdot \cot 45^\circ \cdot \cot 50^\circ \cdots \cot 85^\circ
\]
Simetrik olarak gruplarsak:
\[
= \cot 5^\circ \cdot \cot 10^\circ \cdots \cot 40^\circ \cdot \cot 45^\circ \cdot \cot 50^\circ \cdots \cot 85^\circ
\]
\[
=\cot 5^\circ \cdots \cot 40^\circ \cdot \cot 45^\circ \cdot \underbrace{ \tan 40^\circ}_{\text{ Birbirini 90° tamamlayan açılar} \cot 50° = \tan 40°} \cdot \tan 5^\circ
\]
\[
= 1 \cdot 1 \cdot \cdots \cdot 1 \cdot 1 = 1
\]
\(\textbf{Cevab: E} \)
SORU 19
A, B ve C bir üçgenin açıları olmak üzere,
\[
\frac{ \cos^2\left( \frac{A + B}{2} \right) + \cos^2\left( \frac{C}{2} \right) }
{ \cot\left( \frac{A + B}{2} \right) \cdot \cot\left( \frac{C}{2} \right) }
\]
ifadesinin değeri kaçtır?
\[
\text{A) } 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]
Çözüm:
Üçgenin iç açıları toplamı:
\[
A + B + C = 180^\circ \Rightarrow \frac{A + B}{2} = \frac{180^\circ – C}{2} = 90^\circ – \frac{C}{2}
\]
İfade şu hale gelir:
\[
\frac{ \cos^2\left(90^\circ – \frac{C}{2} \right) + \cos^2\left( \frac{C}{2} \right) }
{ \cot\left(90^\circ – \frac{C}{2} \right) \cdot \cot\left( \frac{C}{2} \right) }
\]
Trigonometrik dönüşüm:
\[
\cos(90^\circ – x) = \sin x,\quad \cot(90^\circ – x) = \tan x
\]
Uygulayalım:
\[
= \frac{ \sin^2\left( \frac{C}{2} \right) + \cos^2\left( \frac{C}{2} \right) }
{ \tan\left( \frac{C}{2} \right) \cdot \cot\left( \frac{C}{2} \right) }
\]
\[
= \frac{1}{1} = 1
\]
\(\textbf{Cevab: A} \)
SORU 20
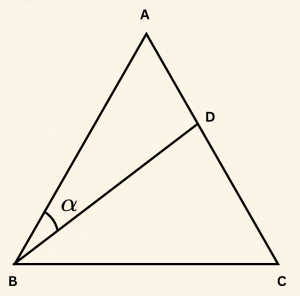
Yandaki şekilde ABC üçgeni eşkenardır.
\[
m(\hat{ ABD}) = \alpha,\quad \frac{ |AD| }{ |DC| } = \frac{2}{3}
\]
olduğuna göre, \(\tan \alpha\) aşağıdakilerden hangisidir?
\[
\text{A) } \frac{\sqrt{3}}{2} \quad
\text{B) } \frac{\sqrt{3}}{3} \quad
\text{C) } \frac{\sqrt{3}}{4} \quad
\text{D) } \frac{\sqrt{3}}{5} \quad
\text{E) } \frac{\sqrt{3}}{6}
\]
Çözüm:
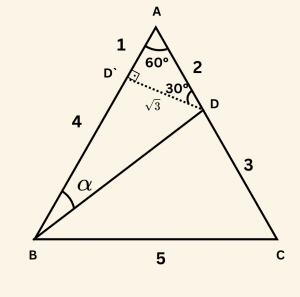 \[\frac{AD}{DC} = \frac{2}{3} \Rightarrow AD = 2, \quad DC = 3 \quad \text{(oranı kolaylaştırmak için)}
\[\frac{AD}{DC} = \frac{2}{3} \Rightarrow AD = 2, \quad DC = 3 \quad \text{(oranı kolaylaştırmak için)}
\]
Eşkenar üçgende:
\[
m(\hat A) = 60^\circ
\]
\([AB]\) üzerine \([DD´]\)dikme inerse:
\[
m ( \hat {ADD´}) = 30^\circ \quad \text{olur }
\]
Bu dik üçgende:
\[
|DD’| = \sqrt{3}, \quad |AD’| = 1 \;\; \text{ birim} \quad \text{(30-60-90 üçgeni oranları)}
\]
Toplam:
\[
|BD| = |AD’ + DB| = 1 + 3 = 4
\]
\[
\tan \alpha = \frac{ |DD’| }{ |BD| } = \frac{\sqrt{3}}{4}
\]
\(\textbf{Cevab: C} \)
SORU 21
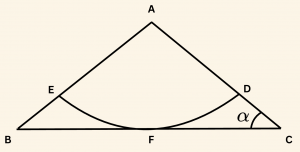 Yandaki şekilde \(A\) noktası dörtte bir çember yayının merkezidir.
Yandaki şekilde \(A\) noktası dörtte bir çember yayının merkezidir.
\[
m(\hat C) = \alpha, \quad \frac{ |AE| }{ |EB| } = 3
\]
ve \([ BC ]\) kenarı \(F\) noktasında \(EFD\) yayına teğet ise \(\cot \alpha\) aşağıdakilerden hangisidir?
\[
\text{A) } \frac{1}{\sqrt{7}} \quad
\text{B) } \frac{2}{\sqrt{7}} \quad
\text{C) } \frac{3}{\sqrt{7}} \quad
\text{D) } \frac{4}{\sqrt{7}}\quad
\text{E) } \frac{5}{\sqrt{7}}
\]
Çözüm:
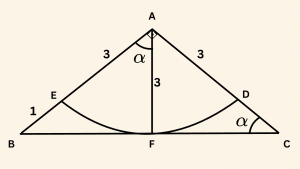
A noktası dörtte bir çemberin merkezi olduğundan:
\[
\hat {BAC} = 90^\circ
\]
F noktası teğet noktası olduğundan, merkezden teğete çizilen dikme F’den geçer ve:
\[
\hat {BAF }= \alpha
\]
Verilen oran:
\[
\frac{|AE|}{|EB|} = 3 \Rightarrow |AE| = 3,\quad |EB| = 1
\]
BAF dik üçgeninde Pisagor uygularsak:
\[
|BA|^2 = |AF|^2 + |BF|^2 \Rightarrow 4^2 = 3^2 + |BF|^2 = \sqrt{7}
\]
Ancak görselde:
\[
|AE| = 3,\quad |EB| = 1 \Rightarrow |AF| = 3,\quad |BF| = \sqrt{7}
\]
Dolayısıyla:
\[
\cot \alpha = \frac{|AF|}{|BF|} = \frac{3}{\sqrt{7}}
\]
\(\textbf{Cevab: C} \)
SORU 22
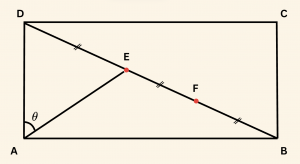
Üsteki şekilde verilen ABCD dikdörtgeninde:
\[
|DE| = |EF| = |FB|,\quad m\hat {DAE} = \theta,\quad |AB| = 3 |AD|
\]
olduğuna göre, \(\sin \theta\) aşağıdakilerden hangisidir?
\[
\text{A) } \frac{1}{\sqrt{10}} \quad
\text{B) } \frac{2}{\sqrt{10}} \quad
\text{C) } \frac{2}{\sqrt{13}} \quad
\text{D) } \frac{3}{\sqrt{13}}\quad
\text{E) } \frac{4}{\sqrt{13}}
\]
Çözüm:
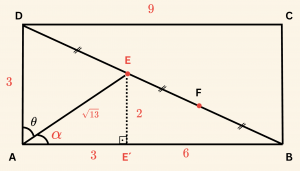
\[
|AD| = 3 \text{ birim alınırsa } \Rightarrow |AB| = 9 \text{ birim olur.}
\]
\([AB]\) üzerine \([EE’]\) dikmesi inilsin.
Üçgenler benzer: \(\triangle DAB \sim \triangle EE’B\) ve
\[ \frac{|AB|}{|E’B|} = \frac{ |DA| }{ |EE´| } = \frac{|DB|}{|EB|} \Rightarrow \frac{|9|}{|E’B|} = \frac{ 3 }{ |EE´| } = \frac{3}{2} \]
\[|E´B| = 6 \;\; birim, \quad |EE´| = 2 \;\; birim \]
\[ |AE´| =|AB| – |E´B| \Rightarrow |AE´| =9-6= 3 \;\; birimdir. \]
\(AE’E \) dik üçgeninde Pisagor bağıntısından:
\[
|AE| = \sqrt{3^2 + 2^2} = \sqrt{13}
\]
\[
\hat {EAE’} = \alpha \;\; olsun.
\Rightarrow \theta + \alpha = 90^\circ \;\; olduğundan \;\; \Rightarrow \sin \theta = \cos \alpha
\]
O halde \(AE’E \) dik üçgeninden:
\[
\cos \alpha = \frac{ |AE’| }{ |AE| } = \frac{3}{\sqrt{13}} \Rightarrow \sin \theta = \frac{3}{\sqrt{13}}
\]
\(\textbf{Cevab: D} \)
SORU 23
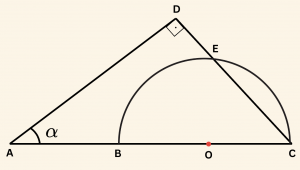 Yandaki şekilde \([ BC ]\) çaplı yarım çemberin merkezi \(O\) dur.
Yandaki şekilde \([ BC ]\) çaplı yarım çemberin merkezi \(O\) dur.
\[
m(\hat A) = \alpha,\quad m(\hat D) = 90^\circ,\quad \frac{ |OB| }{ |EC| } = \frac{3}{4}
\]
olduğuna göre, \(\tan \alpha\) aşağıdakilerden hangisidir?
\[
\text{A) } \frac{2}{\sqrt{5}} \quad
\text{B) } \frac{3}{\sqrt{5}} \quad
\text{C) } \frac{2}{\sqrt{3}} \quad
\text{D) } \frac{1}{3}\quad
\text{E) } \frac{1}{2}
\]
Çözüm:
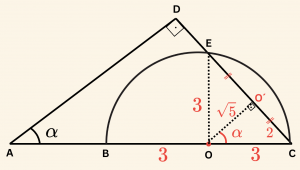 Verilen oran:
Verilen oran:
\[
|OB| = 3 \Rightarrow |EC| = 4
\]
Merkezden \(EC\) kirişi üzerine dikme inildiğinde bu kirişi iki eşit parçaya böler:
\[
|O’C| = 2
\]
\(\triangle DAC \sim \triangle O’OC\) olduğundan:
\[
m(\hat A) = m(\hat {O’OC}) = \alpha
\]
Pisagor bağıntısından:
\[
|OO’| = \sqrt{3^2 – 2^2} = \sqrt{9 – 4} = \sqrt{5}
\]
\[
|O’C| = 2,\quad |OO’| = \sqrt{5}
\]
\[
\tan \alpha = \frac{ |O’C| }{ |OO’| } = \frac{2}{\sqrt{5}}
\]
\(\textbf{Cevab: A} \)
SORU 24

Yandaki şekilde:
\[\frac{|AD|}{|DB|} = \frac{\sqrt{3}}{4},\quad |BC| = 4,\quad \cos \theta = \frac{4}{5}\]
ve \(m(\hat D) = 90^\circ\) olduğuna göre, \(|DC|\) kaç birimdir?
\[
\text{A) } 1 \quad
\text{B) } 2 \quad
\text{C) } \frac{5}{2} \quad
\text{D) } 3\quad
\text{E) } \frac{7}{2}
\]
Çözüm:

\(\triangle CDA\) dik üçgeninde:
\[
\cos \theta = \frac{|DC|}{|AC|} = \frac{4}{5}
\Rightarrow |DC| = 4x,\quad |AC| = 5x
\Rightarrow |AD| = 3x \text{ (Pisagor’dan)}
\]
Verilen oran:
\[
\frac{|AD|}{|DB|} = \frac{\sqrt{3}}{4}
\Rightarrow \frac{3x}{|DB|} = \frac{\sqrt{3}}{4}
\Rightarrow |DB| = \frac{12x}{\sqrt{3}} = 4\sqrt{3}x
\]
BDC dik üçgeninde Pisagor bağıntısından x =
\[
4^2 = (4\sqrt{3}x)^2 + (4x)^2
\Rightarrow x= \frac{1}{2}
\]
ve \[ |DC| = 4x= 4 \cdot \frac{1}{2} = 2 \;\; birimdir \]
\(\textbf{Cevab: B} \)
Uyarı:
Bir dik üçgende, dar açılardan birinin trigonometrik oranı ve herhangi bir kenarın uzunluğu biliniyorsa, diğer kenarların uzunluğu bulunabilir.
Örnek:
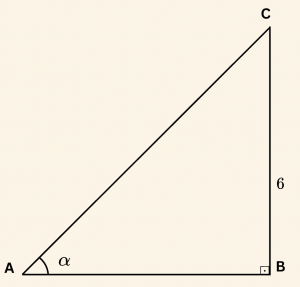
Şekildeki dik üçgende
\[
\tan \alpha = \frac{3}{4}
\]
ve
\[
|BC| = 6 \text{ birim ise }\]
\(AB\) ve \(AC\) kenar uzunluklarını bulalım.
Çözüm:
\[
\tan \alpha = \frac{|BC|}{|AB|} \Rightarrow \frac{3}{4} = \frac{6}{|AB|}
\Rightarrow |AB| = 8 \text{ birim}
\]
Pisagor bağıntısından:
\[
|AC|^2 = |AB|^2 + |BC|^2 = 8^2 + 6^2 = 64 + 36 = 100
\Rightarrow |AC| = 10 \text{ birim bulunur.}
\]
Örnek:
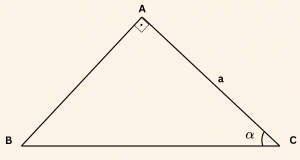
Sekildeki dik üçgende verilenlere göre AB kenar uzunluğunu bulalım.
\[ \tan \alpha = \frac{|AB|}{|AC|} = \frac{|AB|}{a}\]
\( \Rightarrow |AB| = a \cdot \tan \alpha \) olarak bulunur.
SORU 25
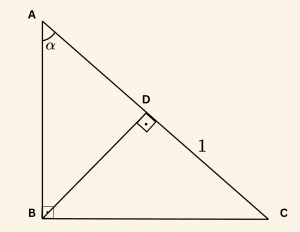 Yandaki şekilde:
Yandaki şekilde:
\[\begin{aligned} &m(\hat{ BDC}) = 90^\circ,\quad \\
&m(\hat {ABC}) = 90^\circ,\quad\\
&m(\hat{ BAD}) = \alpha,\quad\text{ve } \\ &|DC| = 1 \end{aligned} \]
ise \(|AB|\) aşağıdakilerden hangisine eşittir?
\[
\text{A) } \frac{\cot \alpha}{\sin \alpha} \quad
\text{B) } \frac{\tan \alpha}{\cos \alpha} \quad
\text{C) } \tan \alpha \quad
\text{D) } \cot \alpha\quad
\text{E) } \sin \alpha \cdot \cos \alpha
\]
Çözüm:
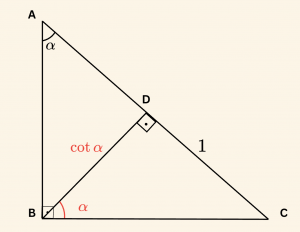 \(\triangle BDC\) dik üçgeninde:
\(\triangle BDC\) dik üçgeninde:
\[
\cot \alpha = \frac{|BD|}{|DC|} = \frac{|BD|}{1}
\Rightarrow |BD| = \cot \alpha
\]
\(\triangle ADB\) dik üçgeninde:
\[
\sin \alpha = \frac{|BD|}{|AB|} = \frac{\cot \alpha}{|AB|}
\Rightarrow |AB| = \frac{\cot \alpha}{\sin \alpha}
\]
\(\textbf{Cevab: A} \)
SORU 26
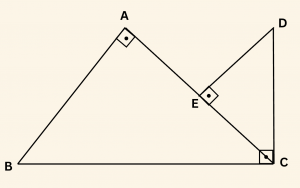
Yandaki şekilde:
– \([AB] \perp [BC]\)
– \([DE] \perp [EC]\)
– \([AC] \perp [CD]\)
\[m(\hat{ CDE}) = \alpha,\quad |AC| = |CD| = 1 \;\; \text{birim} \]
ise \(|BE|\) aşağıdakilerden hangisine eşittir?
\[
\text{A) } \tan \alpha \; – \; \sin \alpha \quad
\text{B) } 1 \; – \; \tan \alpha \quad
\text{C) } \sin \alpha \;- \;\cos \alpha\quad
\text{D) } 1 \;- \;\cot \alpha\quad
\text{E) } \cos \alpha \;- \; \sin \alpha
\]
Çözüm:
\(\triangle DEC\) dik üçgeninden:
\[
\sin \alpha = \frac{|EC|}{|DC|} = \frac{|EC|}{1}
\Rightarrow |EC| = \sin \alpha
\]
\(\triangle ABC\) dik üçgeninden:
\[
\cos \alpha = \frac{|BC|}{|AC|} = \frac{|BC|}{1}
\Rightarrow |BC| = \cos \alpha
\]
Bu durumda:
\[
|BE| = |BC| – |EC| = \cos \alpha – \sin \alpha
\]
\(\textbf{Cevab: E} \)
Uyarı:
Bir açının trigonometrik oranlarından herhangi birisi biliniyorken bu açının diğer trigonometrik oranları, dik üçgen yardımıyla bulunabilir.
SORU 27
\(0^\circ < x < 90^\circ\) olmak üzere,
\[
\frac{\sin^2 x – \cos^2 x}{(\sin x + \cos x)^2} = \frac{1}{2}
\]
olduğuna göre, \(\sin x\) değeri nedir?
\[
\text{A) } \frac{3}{\sqrt{5}} \quad
\text{B) } \frac{2}{\sqrt{5}} \quad
\text{C) } \frac{1}{\sqrt{5}} \quad
\text{D) } \frac{3}{\sqrt{10}}\quad
\text{E) } \frac{1}{\sqrt{5}}
\]
Çözüm:
\[
\frac{\sin^2 x – \cos^2 x}{(\sin x + \cos x)^2} = \frac{1}{2}
\]
\[
\Rightarrow \frac{(\sin x – \cos x)(\sin x + \cos x)}{(\sin x + \cos x)^2} = \frac{1}{2}
\Rightarrow \frac{\sin x – \cos x}{\sin x + \cos x} = \frac{1}{2}
\]
İçler dışlar çarpımı:
\[\begin{aligned} &2(\sin x – \cos x) = \sin x + \cos x \\ \\
\Rightarrow &2\sin x – 2\cos x = \sin x + \cos x \\ \\
\Rightarrow &\sin x = 3\cos x \\\\
\Rightarrow& \frac{\sin x}{\cos x } = 3 \end{aligned}\]
Trigonometrik özdeşlik:
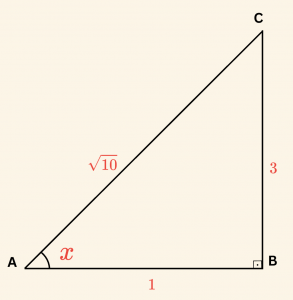
Yukarıdaki dik üçgende
\( m \hat (A) = x \)
\( |BC|= 3 \) birim
\( |AB|= 1 \) birim, seçilerek Pisagor bağıntısından \( |AC| = 10 \) birim bulunur. O halde
\[
\sin x = \frac{|BC|}{|AC|} = \frac{3}{\sqrt{10}}
\]
\(\textbf{Cevab: D} \)
SORU 28
\( B \) dar açı olmak üzere,
\[
A + B = 30^\circ \quad \text{ve} \quad \cos(3A + 2B) = \frac{3}{5}
\]
ise \(\tan B\) değeri kaçtır?
\[
\text{A) } 2\quad
\text{B) } \frac{3}{2} \quad
\text{C) } \frac{2}{3} \quad
\text{D) } \frac{4}{3} \quad
\text{E) } \frac{3}{4}
\]
Çözüm:
\[
A + B = 30^\circ \Rightarrow A = 30^\circ – B
\]
\[
\cos(3A + 2B) = \frac{3}{5}
\Rightarrow \cos\left[3(30^\circ – B) + 2B\right] = \frac{3}{5}
\Rightarrow \cos(90^\circ – B) = \frac{3}{5}
\]
\[
\cos(90^\circ – B) = \sin B \Rightarrow \sin B = \frac{3}{5}
\]

Şimdi trigonometrik tanjant oranını bulmak için bir dik üçgen çizelim:
\[
\tan x = \frac{\text{karşı}}{\text{komşu}} = \frac{3}{4}
\]
\(\textbf{Cevab: E} \)
SORU 29
\(0 < x < \frac{\pi}{2}\) olmak üzere,
\[
2 \sin x – \cos x = 1
\]
ise \(\sin x\) in değeri nedir?
\[
\text{A) } \frac{4}{5}\quad
\text{B) } \frac{3}{5} \quad
\text{C) } \frac{2}{5} \quad
\text{D) } \frac{1}{5} \quad
\text{E) } \frac{1}{6}
\]
Çözüm 1:
Verilen eşitliğin her iki tarafının karesi alınır:
\[
(2 \sin x – \cos x)^2 = 1^2 \]
\[\Rightarrow 4 \sin^2 x + \cos^2 x – 4 \sin x \cos x = 1
\]
\[ \Rightarrow 3 \sin^2 x + \underbrace{\sin^2 x + \cos^2 x }_{1} – 4 \sin x \cos x = 1 \]
\[
\Rightarrow 3 \sin^2 x – 4 \sin x \cos x = 0\]
\[\Rightarrow \sin x (3 \sin x – 4 \cos x) = 0
\]
\[
\Rightarrow 3 \sin x – 4 \cos x = 0 \quad (\text{çünkü } \sin x \ne 0)
\Rightarrow \tan x = \frac{4}{3}
\]
 Dik üçgen çizilirse:
Dik üçgen çizilirse:
Karşı = 4, Komşu = 3, Hipotenüs = 5
\[
\sin x = \frac{4}{5}
\]
Çözüm 2:
\[2 \sin x – \cos x = 1\]
\[ \Rightarrow 2 \sin x – \sqrt{1 – \sin^2 x} = 1 \]
Her iki tarafın karesi alınır:
\[(2 \sin x – 1)^2 = (\sqrt{ 1 – \sin^2 x})^2\]
\[\Rightarrow 4 \sin^2 x – 4 \sin x + 1 = 1 – \sin^2 x\]
\[\Rightarrow 5 \sin^2 x – 4 \sin x = 0\]
\[\Rightarrow \sin x (5 \sin x – 4) = 0\]
\[\Rightarrow \sin x = \frac{4}{5} \quad (\sin x \neq 0 )\]
\(\textbf{Cevab: A} \)
<p style=”text-align: center;”>← Önceki Sayfa | Sonraki Sayfa →</p>