Kosinüs Teoremi

 

Kosinüs Teoremi

 

Bir \(ABC\) üçgeninin kenarları \(a\), \(b\), \(c\) ise,

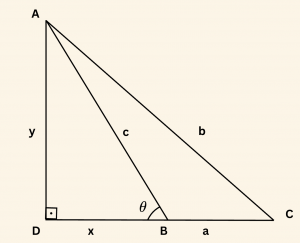
ADB dik üçgeninde

\[
\cos \theta = -\cos B = \frac{x}{c}
\]
ve Pisagor bağıntısından,
\[
x^2 + y^2 = c^2 \text{ dir.}
\]

ADC dik üçgeninde Pisagor bağıntısından,

\[
(x + a)^2 + y^2 = b^2
\]
\[
\Rightarrow x^2 + a^2 + 2ax + y^2 = b^2
\]
\[
\Rightarrow x^2 + y^2 + 2ax + a^2 = b^2
\]
\[
\Rightarrow c^2 + 2a(-c \cos B) + a^2 = b^2
\]
\[
\Rightarrow b^2 = a^2 + c^2\; -\; 2ac \cos B
\]

O halde,

\[
\begin{aligned}
a^2 &= b^2 + c^2 \;-\; 2bc \cos A \\ \\
b^2 &= a^2 + c^2 \;- \;2ac \cos B \\ \\
c^2 &= a^2 + b^2 \;-\; 2ab \cos C
\end{aligned}
\]

 

Sonuçlar:

1. Bir üçgenin iki kenarı ile bir açısı biliniyorsa bu üçgenin üçüncü kenarı kosinüs teoreminden bulunabilir.

2. Bir üçgenin üç kenarının uzunluğu biliniyorsa bu üçgenin herhangi bir açısının ölçüsü, kosinüs teoreminden bulunabilir.

 

Örnek:

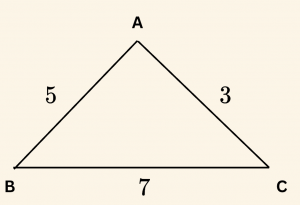Yandaki şekilde verilenlere göre \(\cos A\) nın değerini bulalım.

ABC üçgeninde kosinüs teoremi yazılırsa,

\[7^2=  5^2 + 3^2- 2 \cdot  5 \cdot  3 \cos A    \]

\[ \Rightarrow \cos A= – \frac{1}{2} \] olarak bulunur

 

 

Örnek:

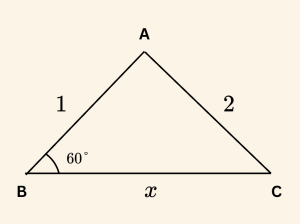 Yandaki şekilde verilenlere göre \(|BC| = x\) uzunluğunu bulalım.

ABC üçgeninde kosinüs teoremi yazılırsa,

\[
2^2 = 1^2 + x^2 – 2 \cdot 1 \cdot x \cdot \cos 60^\circ
\]

 

 

\[
\Rightarrow 4 = 1 + x^2 – 2x \cdot \frac{1}{2}
\Rightarrow x^2 – x – 3 = 0
\]
\[
\Rightarrow x = \frac{1 + \sqrt{13}}{2} \quad \text{dir.}
\]

 

SORU 38

Bir üçgenin kenar uzunlukları \(a, b, c\) arasında
\[
b + c \;- \;a = \frac{bc}{a + b + c}
\]
bağıntısı varsa bu üçgenin \(A\) açısının ölçüsü kaç derecedir?

\[
\text{A) } 45 \quad
\text{B) } 60 \quad
\text{C) } 90 \quad
\text{D) } 120  \quad
\text{E) } 150
\]

 

Çözüm:

\[
b + c\; – \;a = \frac{bc}{a + b + c}
\Rightarrow (b + c \;-\; a)(a + b + c) = bc
\]

\[\begin{aligned} \Rightarrow (b + c)^2 \;- a^2 = bc \\ \\
\Rightarrow b^2 + c^2 + 2bc\; – a^2 = bc \\ \\
\Rightarrow a^2 = b^2 + c^2 + bc \end{aligned}\]

ABC üçgeninde kosinüs teoremi yazılırsa,

\[\begin{aligned} a^2 = b^2 + c^2 \;- \;2bc \cos A \\ \\
\Rightarrow b^2 + c^2 + bc = b^2 + c^2 \;- \;2bc \cos A \\ \\
\Rightarrow bc = -2bc \cos A \end{aligned}\]

\[\begin{aligned} \Rightarrow \cos A = -\frac{1}{2} \\ \\
\Rightarrow m(\hat A) = 120^\circ \quad \text{dir.}   \end{aligned}\]

\(\textbf{Cevab: D} \)

 

SORU 39

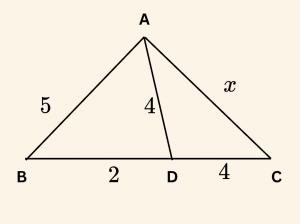
Yandaki şekilde
\(|AB| = 5\) cm,
\(|BD| = 2\) cm,
\(|AD| = |DC| = 4\) cm

ise \(|AC| = x\) kaç cm’dir?

 

 

\[
\text{A) } \sqrt{19} \quad
\text{B) } 2\sqrt{5} \quad
\text{C) } \sqrt{21} \quad
\text{D) } \sqrt{22}  \quad
\text{E) } \sqrt{23}
\]

 

Çözüm:

ABD üçgeninde kosinüs teoremi:

\[
4^2 = 5^2 + 2^2 – 2 \cdot 5 \cdot 2 \cdot \cos B
\Rightarrow \cos B = \frac{13}{20}
\]

ABC üçgeninde tekrar kosinüs teoremi:

\[
x^2 = 5^2 + 6^2 – 2 \cdot 5 \cdot 6 \cdot \frac{13}{20}
\Rightarrow x^2 = 22
\Rightarrow x = \sqrt{22}
\]

\(\textbf{Cevab: D} \)

 

SORU 40

 

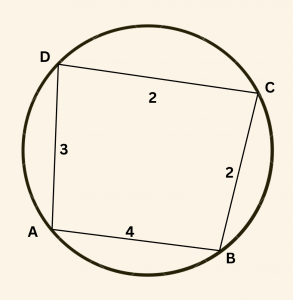
Yandaki şekilde ABCD kirişler dörtgenidir.

\(|AB| = 4\) cm, \(|BC| = |CD| = 2\) cm, \(|AD| = 3\) cm

olduğuna göre, \(\cos A\) nın değeri nedir?

 

 

 

\[
\text{A) } \frac{15}{32} \quad
\text{B) } \frac{1}{2} \quad
\text{C) }\frac{17}{32} \quad
\text{D) }\frac{9}{16} \quad
\text{E) } \frac{19}{32}
\]

 

Çözüm:

Kirişler dörtgeninde karşılıklı açılar bütünler olduğundan

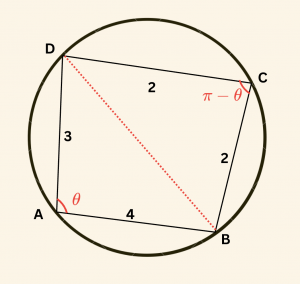
\[m(\hat A) + m(\hat C )= \pi \]
\[\Rightarrow m( \hat C )= \pi \;- \; \theta\]

ADB ve CDB üçgenlerinde kosinüs teoremi:

\[\begin{aligned} |BD|^2 &= 3^2 + 4^2 – 2 \cdot 3 \cdot 4 \cdot \cos \theta \\ \\ |BD|^2 &= 25 -24\cos \theta   \end{aligned}\]

 

\[
|BD|^2 = 3^2 + 4^2 – 2 \cdot 3 \cdot 4 \cdot \cos \theta
\]

\[
|BD|^2 = 2^2 + 2^2 – 2 \cdot 2 \cdot 2 \cdot \cos(\pi – \theta)\]
\[\Rightarrow \cos(\pi – \theta) = -\cos \theta \\
\]

\[\\ |BD|^2 = 8 + 8 \cos \theta \ \]

Eşitleyip çözersek:

\[\begin{aligned} 25 \;- \; 24 \cos \theta = 8 + 8 \cos \theta \\ \\
\Rightarrow 17 = 32 \cos \theta \\ \\
\Rightarrow \cos \theta = \frac{17}{32} \end{aligned}\]

\(\textbf{Cevab: C} \)

 

SORU 41

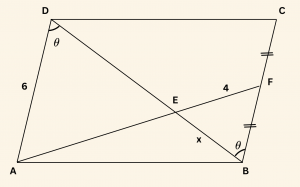Yandaki şekilde
ABCD dörtgeni paralelkenardır.

\(|EF| = 4\) cm,
\(|AD| = 6\) cm,
\(|CF| = |FB|\),
\(m(\hat{ ADE}) = \theta\) ve \(\cos \theta = \frac{1}{3}\)

olduğuna göre,
\(|EB| = x\) kaç cm’dir?

\[\text{A) } 1 + 2\sqrt{2} \quad
\text{B) } 2 + \sqrt{2} \quad
\text{C) } \sqrt{2} \quad
\text{D) }  2\sqrt{2} \quad
\text{E) } 3 – \sqrt{2}
\]

 

 

Çözüm:

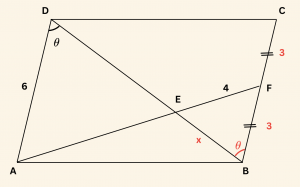Paralelkenarda karşılıklı kenarlar eşit olduğundan:
\[
|AD| = |BC| = 6, \quad |FB| = 3
\]

Verilen açıya göre:
\[
m(\hat {ADE}) = m(\hat {EBF}) = \theta
\]

EBF üçgeninde kosinüs teoremi yazılırsa,

\[\begin{aligned} 4^2 &= x^2 + 3^2\; – \; 2 \cdot x \cdot 3 \cdot \cos \theta \\ \\
\Rightarrow 16 &= x^2 + 9 \;- \; 6x \cdot \frac{1}{3}  \\ \\ \Rightarrow  16 &= x^2 + 9 \; – \;2x \\ \\    \Rightarrow  0&=x^2\; -\; 2x\; -\; 7  \\ \\ \Rightarrow x& = 1 + 2\sqrt{2} \end{aligned} \]

\(\textbf{Cevab: A} \)

 

SORU 42

 

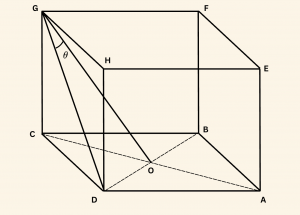
Yandaki şekilde $ABCDEFGH$ bir küp ise, $m(\hat{ DGO}) = \theta$ kaç derecedir?

 

 

 

\[\text{A) } 15 \quad
\text{B) } 30 \quad
\text{C) } 45 \quad
\text{D) }  60 \quad
\text{E) } 75
\]

 

 

 

Çözüm:

Küpün bir kenarı $2$ birim olsun.

ABCD karesinde:
\[
|AC| = |BD| = 2\sqrt{2} \Rightarrow |OD| = |OC| = \sqrt{2}
\]

GCO dik üçgeninde Pisagor bağıntısı uygulanırsa:
\[
|GC|^2 + |OC|^2 = |OG|^2 \Rightarrow 2^2 + (\sqrt{2})^2 = |OG|^2 \Rightarrow |OG| = \sqrt{6}
\]

GCD dik üçgeninde Pisagor uygulanırsa:
\[
|GC|^2 + |CD|^2 = |GD|^2 \Rightarrow 2^2 + 2^2 = |GD|^2 \Rightarrow |GD| = 2\sqrt{2}
\]

GDO üçgeninde kosinüs teoremi uygulanırsa
\[
|OD|^2 = |GD|^2 + |OG|^2 – 2|GD| \cdot   |OG|\cos\theta
\]

Değerler yerine yazılır:
\[
2 = 8 + 6 – 2 \cdot 2\sqrt{2} \cdot \sqrt{6} \cdot \cos\theta
\Rightarrow 2 = 14 – 4\sqrt{12} \cdot \cos\theta
\]

$\sqrt{12} = 2\sqrt{3}$ olduğundan:
\[
2 = 14 – 8\sqrt{3} \cos\theta
\Rightarrow 8\sqrt{3} \cos\theta = 12 \Rightarrow \cos\theta = \frac{3}{2\sqrt{3}} = \frac{\sqrt{3}}{2}
\Rightarrow \theta = 30^\circ
\]

\(\textbf{Cevab: B} \)