Trigonometrik Toplam Ve Fark Formülleri

 

Trigonometrik Toplam Ve Fark Formülleri

 

 

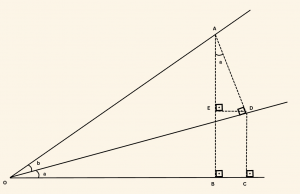
Yukarıdaki şekilde
\[m( \hat {COD} )= a \;\; ve \;\; m(\hat{ DOA}) = b \] açıların toplamı
\[m(\hat{ COA}) = a + b \;\; olur. \]

ABO dik üçgeninden,

\[
\sin (a + b) = \frac{|AB|}{|OA|} = \frac{|EB|}{|OA|} + \frac{|AE|}{|OA|} = \frac{|DC| + |AE|}{|OA|}
\]

DCO dik üçgeninden,

\[
\sin a = \frac{|DC|}{|OD|} \Rightarrow |DC| = |OD| \cdot \sin a
\]

ADO dik üçgeninden,

\[
\cos b = \frac{|OD|}{|OA|} \Rightarrow |OD| = |OA| \cdot \cos b
\]

Bu ifade yerine yazılırsa,

\[
|DC| = |OA| \cdot \sin a \cdot \cos b
\] bulunur

AED dik üçgeninden,

\[
\cos a = \frac{|AE|}{|AD|} \Rightarrow |AE| = |AD| \cdot \cos a
\]

ADO dik üçgeninden,

\[
\sin b = \frac{|AD|}{|OA|} \Rightarrow |AD| = |OA| \cdot \sin b
\]

Bu ifade yerine yazılırsa,

\[
|AE| = |OA| \cdot \sin b \cdot \cos a
\] bulunur.

O halde,

\[
\sin (a + b) = \frac{|DC| + |AE|}{|OA|} = \frac{|OA| \cdot \sin a \cdot \cos b + |OA| \cdot \sin b \cdot \cos a}{|OA|}
\]

\[
\sin (a + b) = \sin a \cdot \cos b + \sin b \cdot \cos a
\] olur

\[ 1. \quad \sin (a + b) = \sin a \cos b + \sin b \cos a  \]

Bir numaralı formülde b  yerine  -b  yazılırsa,

\[ 2. \quad \sin (a – b) = \sin a \cos b \;- \; \sin b \cos a  \]

 

Cos için:

İki numaralı formülde  a  yerine \( \frac{\pi}{2} – a \)  yazılırsa,

\[ 3. \quad \cos (a + b) = \cos a \cos b \; – \; \sin a \sin b \]

Üç numaralı formülde  b yerine  -b  yazılırsa,

\[ 4. \quad \cos (a \; – \; b) = \cos a \cos b + \sin a \sin b  \]

 

Tanjant için:

\[
\tan (a + b) = \frac{\sin (a + b)}{\cos (a + b)} = \frac{\sin a \cos b + \sin b \cos a}{\cos a \cos b \; – \; \sin a \sin b}
\]

Pay ve payda \(  \cos a \cdot \cos b \)  ile bölünürse,

\[ 5. \quad \tan (a + b) = \frac{\tan a + \tan b}{1 – \tan a \cdot \tan b}  \]

Beş numaralı formülde  b  yerine  -b  yazılırsa,

\[ 6. \quad \tan (a – b) = \frac{\tan a \; – \;\tan b}{1 + \tan a \cdot \tan b}  \]

Kotanjant için

\[
\cot (a + b) = \frac{\cos (a + b)}{\sin (a + b)} = \frac{\cos a \cdot \cos b \;- \; \sin a \cdot \sin b}{\sin a \cdot \cos b + \sin b \cdot \cos a}
\]

Pay ve payda \(  \sin a \cdot \sin b \)  ile bölünürse,

\[ 7. \quad \cot (a + b) = \frac{\cot a \cdot \cot b \;- \;1}{\cot a + \cot b}  \]

Yedi numaralı formülde b yerine  -b  yazılırsa,

\[ 8. \quad \cot (a – b) = \frac{\cot a \cdot \cot b + 1}{\cot b \;- \; \cot a} \]

 

Tablo olarak vermek gerekirse,

\[
\begin{array}{| l | }
\hline \\
1. \quad \sin (a + b) = \sin a \cos b + \sin b \cos a  \\ \\
\hline \\
2. \quad \sin (a \; – \; b) = \sin a \cos b \;- \; \sin b \cos a \\ \\
\hline \\
3. \quad \cos (a + b) = \cos a \cos b \; – \; \sin a \sin b \\ \\
\hline \\
4. \quad \cos (a \; – \; b) = \cos a \cos b + \sin a \sin b  \\ \\
\hline \\
5. \quad \tan (a + b) = \Large \frac{\tan a + \tan b}{1 – \tan a \cdot \tan b} \\ \\
\hline \\
6. \quad \tan (a \;- \; b) = \Large \frac{\tan a \; – \;\tan b}{1 + \tan a \cdot \tan b} \\ \\
\hline \\
7. \quad \cot (a + b) = \Large \frac{\cot a \cdot \cot b \;- \;1}{\cot a + \cot b} \\ \\
\hline \\
8. \quad \cot (a\; – \; b) =  \Large \frac{\cot a \cdot \cot b + 1}{\cot b \;- \; \cot a} \\ \\
\hline
\end{array}
\]

 

Uyarı:

\( \text{cot} (a \pm b) \text{ yi bulmak için, } \tan (a \pm b) \)  bulunup çarpmaya göre tersi alınır.
\[
\cot (a \pm b) = \frac{1}{\tan (a \pm b)} \text{ dir.}
\]

Örnek:

\( \sin 75° \)    ile   \( \cot 15° \)   yi hesaplayalım.

\[
\sin 75^\circ = \sin (45^\circ + 30^\circ) = \sin 45^\circ \cdot \cos 30^\circ + \sin 30^\circ \cdot \cos 45^\circ
\]

\[
= \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{1}{2} \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{6} + \sqrt{2}}{4} \text{ tür.}
\]

\( \cot 15° \)  yi hesaplamak için önce tan 15°’yi hesaplayalım.

\[
\tan 15^\circ = \tan (60^\circ – 45^\circ) = \frac{\tan 60^\circ – \tan 45^\circ}{1 + \tan 60^\circ \cdot \tan 45^\circ} = \frac{\sqrt{3} – 1}{1 + \sqrt{3} \cdot 1}
\]

\[
\cot 15^\circ = \frac{1}{\tan 15^\circ} = \frac{1 + \sqrt{3}}{\sqrt{3} – 1} = 2 + \sqrt{3} \text{ tür.}
\]

 

SORU 1

\( \tan 65^\circ = a \text{ ise } \tan 40^\circ \text{ nin } a \)  cinsinden değeri nedir?

\[
\text{A) } \frac{1 – a^2}{a} \quad \text{B) } \frac{1 – a^2}{2a} \quad \text{C) } \frac{a^2 – 1}{2a} \quad \text{D) } \frac{a^2 + 1}{a} \quad \text{E) } \frac{a^2 + 1}{2a}
\]

 

Çözüm:

\( \tan 65^\circ = a \Rightarrow \cot 25^\circ = a \Rightarrow \tan 25^\circ = \frac{1}{a} \)

\[
\tan 40^\circ = \tan (65^\circ – 25^\circ) = \frac{\tan 65^\circ – \tan 25^\circ}{1 + \tan 65^\circ \cdot \tan 25^\circ} = \frac{a – \frac{1}{a}}{1 + a \cdot \frac{1}{a}} = \frac{a^2 – 1}{2a} \text{ dir.}
\]

\(\textbf{Cevab: C} \)

 

SORU 2

\( \text{cot } x = 3 \text{ ve tan } y = -2 \text{ ise } x + y \) aşağıdakilerden hangisidir?

\[
\text{A) } 135^\circ \quad \text{B) } 150^\circ \quad \text{C) } 225^\circ \quad \text{D) } 240^\circ \quad \text{E) } 300^\circ
\]

Çözüm:

\[\begin{aligned} &\tan y = -2 \\ \\
& \cot x = 3 \Rightarrow \tan x = \frac{1}{3}   \end{aligned}\]

\[
\tan (x + y) = \frac{\tan x + \tan y}{1 – \tan x \cdot   \tan y} = \frac{\frac{1}{3} + (-2)}   {1 – \frac{1}{3} \cdot (-2)} = \frac{-\frac{5}{3}}{1 + \frac{2}{3}} = \frac{-\frac{5}{3}}{\frac{5}{3}} = -1
\]

\[
\text{tan } (x + y) = -1 \Rightarrow x + y = 135^\circ
\]

\(\textbf{Cevab: A} \)

 

SORU 3

Bir ABC üçgeninde,

\( (\sin A + \cos B)^2 + (\cos A + \sin B)^2 = 3  \) ise C açısının ölçüsü aşağıdakilerden hangisidir?

\[
\text{A) } 60^\circ \quad \text{B) } 90^\circ \quad \text{C) } 120^\circ \quad \text{D) } 135^\circ \quad \text{E) } 150^\circ
\]

 

Çözüm:

\[\begin{aligned}
(\sin A + \cos B)^2  & = \sin^2 A + \cos^2 B + 2 \sin A \cos B \\ \\
(\cos A + \sin B)^2   &=  \cos^2 A + \sin^2 B + 2 \cos A \sin B \\ \\
+ \quad \quad   3 & =  1 + 1 + 2 (\sin A \cos B + \cos A \sin B) \\
\hline
\end{aligned}\]

\[
\Rightarrow \frac{1}{2} = \sin (A + B)
\]

\[
\Rightarrow A + B = 30^\circ \text{ veya } A + B = 150^\circ
\]

\[
\text{ve } A + B + C = 180^\circ \text{ olduğundan,}
\]

\[
C = 150^\circ \text{ veya } C = 30^\circ \text{ dir.}
\]

\(\textbf{Cevab: E} \)

 

SORU 4

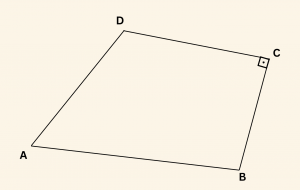Yandaki şekilde  \( m \hat{C} = 90° \)

\[ \tan A = 3 \;\; \text{ ve } \;\; \tan B = -\frac{1}{3} \]  olduğuna göre, \( \sin D \) nedir?

\[
\text{A) } \frac{1}{6} \quad \text{B) } \frac{1}{5} \quad \text{C) } \frac{2}{5} \quad \text{D) } \frac{3}{5} \quad \text{E) } \frac{4}{5}
\]

 

Çözüm:

\( A + B + D = 270^\circ \Rightarrow D = 270^\circ – (A + B) \)
\[ \Rightarrow \cot D = \cot [270^\circ – (A + B)] = \tan (A + B) \]

\[
\tan (A + B) = \frac{\tan A + \tan B}{1 – \tan A \cdot   \tan B} = \frac{3 + \left(-\frac{1}{3}\right)}{1 – 3 \cdot \left(-\frac{1}{3}\right)} = \frac{\frac{8}{3}}{1 + 1} = \frac{4}{3}
\]

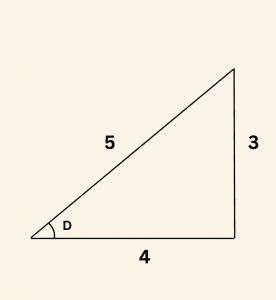
O halde yandaki dik üçgenden,

 

\[
\sin D = \frac{3}{5} \text{ bulunur.}
\]

 

 

 

 

\(\textbf{Cevab: D} \)

 

SORU 5

\[
\frac{\sin \left( x + \frac{\pi}{4} \right)}{\cos \left( x – \frac{\pi}{4} \right)} + \tan \left( x + \frac{\pi}{4} \right) = \frac{1}{2}
\]

ise  \( \tan x   \) nedir?

\[
\text{A) } 2 \quad \text{B) } 1 \quad \text{C) } -2 \quad \text{D) } -3 \quad \text{E) } -4
\]

 

Çözüm:

\[
\frac{\sin \left( x + \frac{\pi}{4} \right)}{\cos \left( x – \frac{\pi}{4} \right)} = \frac{\cos \left[ \frac{\pi}{2} – (x + \frac{\pi}{4}) \right]}{\cos \left[ -(\frac{\pi}{4} – x) \right]} = \frac{\cos \left( \frac{\pi}{4} – x \right)}{\cos \left( \frac{\pi}{4} – x \right)} = 1
\]

\[
\tan \left( x + \frac{\pi}{4} \right) = \frac{\tan x + \tan \frac{\pi}{4}}{1 – \tan x \cdot \tan \frac{\pi}{4}} = \frac{\tan x + 1}{1 – \tan x}
\]

O halde,

\[
\frac{\sin \left( x + \frac{\pi}{4} \right)}{\cos \left( x – \frac{\pi}{4} \right)} + \tan \left( x + \frac{\pi}{4} \right) = \frac{1}{2}
\]

\[
1 + \frac{\tan x + 1}{1 – \tan x} = \frac{1}{2}
\]

\[
\Rightarrow \frac{(1 – \tan x) + (\tan x + 1)}{1 – \tan x} = \frac{1}{2}
\]

\[
\Rightarrow \frac{2}{1 – \tan x} = \frac{1}{2} \Rightarrow  (1 – \tan x) = 4
\]

\[
\Rightarrow 1-  \tan x = 3 \Rightarrow \tan x = -3
\]

\[
\tan x = -3 \text{ tür.}
\]

\(\textbf{Cevab: D} \)

 

SORU 6

\[
\frac{\sin 10^\circ + \sqrt{3} \cos 10^\circ}{\cos 20^\circ} \text{ ifadesinin eşiti nedir?}
\]

\[
\text{A) } 1 \quad \text{B) } 2 \quad \text{C) } 3 \quad \text{D) } 4 \quad \text{E) } 5
\]

Çözüm:

\[
\frac{\sin 10^\circ + \sqrt{3} \cos 10^\circ}{\cos 20^\circ} = \frac{\sin 10^\circ + \tan 60^\circ \cdot \cos 10^\circ}{\cos 20^\circ}
\]

\[
\frac{\sin 10^\circ + \frac{\sin 60^\circ}{\cos 60^\circ} \cdot \cos 10^\circ}{\cos 20^\circ}
\]

\[
= \frac{\sin 10^\circ \cdot \cos 60^\circ + \sin 60^\circ \cdot \cos 10^\circ}{\cos 60^\circ \cdot \cos 20^\circ}
\]

\[
= \frac{\sin (10^\circ + 60^\circ)}{\frac{1}{2} \cdot \cos 20^\circ} = \frac{2 \cdot \sin 70^\circ}{\cos 20^\circ} = 2 \text{ dir.}
\]

\(\textbf{Cevab: B} \)

 

SORU 7

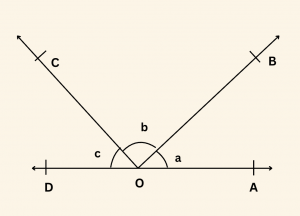Yandaki şekilde

\[\begin{aligned}&m(A\hat{O}B) = a \\ \\
&m( B\hat{O}C) = b \\ \\
&m( C\hat{O}D) = c \;\; \text{ olduğuna göre,}\end{aligned}\]

\[
\tan a + \tan b + \tan c \text{ toplamı aşağıdakilerden hangisine eşittir?}
\]

 

\[
\text{A) } \tan a \cdot \tan b \cdot \tan c \quad
\text{B) } -\tan a \cdot \tan b \cdot \tan c \quad
\text{C) } 0 \quad
\text{D) } -1 \quad
\text{E) } 1
\]

 

Çözüm:

\[
a + b + c = 180^\circ \Rightarrow a + b = 180^\circ – c
\]

\[
\Rightarrow \tan (a + b) = \tan (180^\circ – c) = -\tan c
\]

\[
\Rightarrow \frac{\tan a + \tan b}{1 – \tan a \cdot \tan b} = -\tan c
\]

\[
\Rightarrow \tan a + \tan b = -\tan c + \tan a \cdot \tan b \cdot \tan c
\]

\[
\Rightarrow \tan a + \tan b + \tan c = \tan a \cdot \tan b \cdot \tan c
\]

\(\textbf{Cevab: A} \)

 

Uyarı:

\[
f(x) = a \sin x + b \cos x \text{ fonksiyonunun maksimum ve minimum değerlerini bulalım.}
\]

\[
f(x) = a \sin x + b \cos x
\]

\[
\Rightarrow f(x) = a \left( \sin x + \frac{b}{a} \cos x \right)
\]

Burada  \[ \frac{b}{a} = \tan y = \frac{\sin y}{\cos y}  \text{ denilirse,} \]

\[
f(x) = a \left( \sin x + \frac{\sin y}{\cos y} \cdot \cos x \right)
\]

\[
f(x) = a \left( \frac{\sin x \cdot \cos y + \sin y \cdot \cos x}{\cos y} \right)
\]

\[
f(x) = \frac{a \sin (x + y)}{\cos y}
\]

 

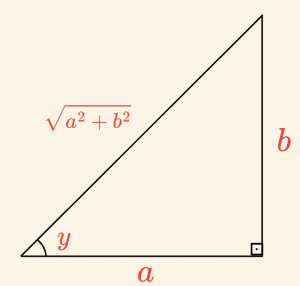Yandaki dik üçgenden,\[
\cos y = \frac{a}{\sqrt{a^2 + b^2}}
\]\[
f(x) = \frac{a \sin (x + y)}{a / \sqrt{a^2 + b^2}}
\]

\[ = \sqrt{a^2 + b^2} \cdot \sin (x + y) \]

 

\[-1 \leq \sin (x + y) \leq 1 \text{ olduğundan,}\]

\[\begin{aligned}
&\sin (x + y) = 1 \;\; \text{için} \quad f_{max} = \sqrt{ a^2+b^2} \\ \\
&\sin (x + y) = 1 \;\; \text{için} \quad f_{min} = -\sqrt{ a^2+b^2} \\ \\
\end{aligned}\]

 

 

SORU 8

\[ f(x) = 3 \sin x \;-\; 4 \cos x \] fonksiyonunun maksimum değeri  \( m \), minimum değeri  \( n  \) ise \(  (m, n)  \)  aşağıdakilerden hangisidir?

\[
\text{A) } (-1, 1) \quad \text{B) } (5, -5) \quad \text{C) } (-4, 3) \quad \text{D) } (-3, 4) \quad \text{E) } (-\sqrt{5}, \sqrt{5})
\]

 

Çözüm:

\[
m = f_{\text{max}} = \sqrt{3^2 + (-4)^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\]

\[
n = f_{\text{min}} = -\sqrt{3^2 + (-4)^2} = -5
\]

\[
(m, n) = (5, -5)
\]

\(\textbf{Cevab: B} \)

 

SORU 9

 

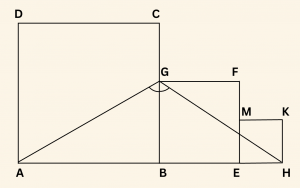
Yandaki şekilde
ABCD,  BEFG ve EHKM birer karedir.

 

 

 

\[ |AB| = 2|BE| = 4|EH| \;\;  \text{olduğuna göre,}   \] \( \tan (\hat{ AGH}) \)  nin değeri nedir?

\[ \text{A) } -\frac{1}{2} \quad \text{B) } -\frac{2}{3} \quad \text{C) } -1 \quad \text{D) } -\frac{3}{2} \quad \text{E) } -\frac{7}{4} \]

 

Çözüm:

\[ m(\hat {AGB} ) = a \;\;  \text{ ve } \;\;  m(\hat{ BGH} ) = b \;\;  \text{ olsun.} \]
\( |EH| = 1 \;\; \) birim seçilirse,

\( |BE| = |BG| = 2 \)  birim,

\(  |AB| = 4  \) birim olur.

ABG dik üçgeninden,

\[
\tan a = \frac{|AB|}{|BG|} = \frac{4}{2} = 2
\]

GBH dik üçgeninden,

\[
\tan b = \frac{|BH|}{|BG|} = \frac{3}{2}
\]

O halde,

\[
\tan (\hat{ AGH} ) = \tan (a + b) = \frac{\tan a + \tan b}{1 – \tan a \cdot   \tan b} = \frac{2 + \frac{3}{2}}{1 – 2 \cdot \frac{3}{2}} = \frac{\frac{7}{2}}{-2} = -\frac{7}{4}
\]

\(\textbf{Cevab: E} \)

 

SORU 10

 

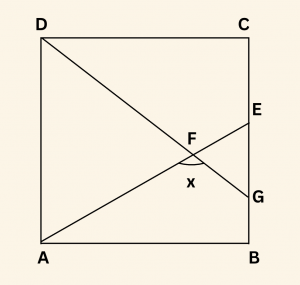
Yandaki şekilde ABCD bir karedir.

\( |EC| = |EG| = 2|GB| \)  ve

\( m(\hat{ AFG}) = x \)  ise,

\( \tan x \) in değeri nedir?

 

\[
\text{A) } -\frac{35}{13} \quad
\text{B) } \frac{35}{13} \quad
\text{C) } \frac{34}{15} \quad
\text{D) } -\frac{13}{15} \quad
\text{E) } -\frac{7}{13}
\]

 

Çözüm:

\[
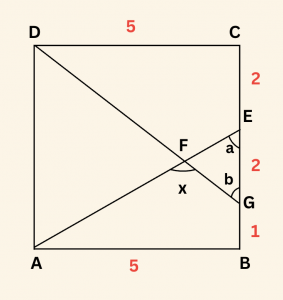m(\hat{ AEG}) = a, \quad m(\hat{ DGE}) = b \;\; \text{ ise } \;\; x = a + b \;\; \text{ dir.}
\]

\( |GB| = 1  \) birim seçilirse,

\( |EG| = |CE| = 2 \)  birim ve

\( |AB| = |DC| = 5  \) birim olur.

ABE dik üçgeninden,

\[
\tan a = \frac{|AB|}{|EB|} = \frac{5}{3}
\]

GCD dik üçgeninden,

\[
\tan b = \frac{|DC|}{|CG|} = \frac{5}{4}
\]

O halde,

\[
\tan x = \tan (a + b) = \frac{\tan a + \tan b}{1 – \tan a \cdot \tan b} = \frac{\frac{5}{3} + \frac{5}{4}}{1 – \frac{5}{3} \cdot \frac{5}{4}}
\]

\[
= \frac{\frac{20 + 15}{12}}{1 – \frac{25}{12}} = \frac{\frac{35}{12}}{-\frac{13}{12}} = -\frac{35}{13}
\]

\(\textbf{Cevab: A} \)

 

SORU 11

 

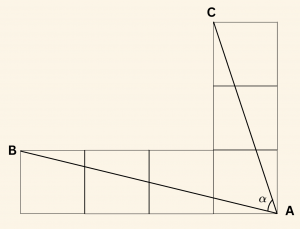
Yandaki şekil altı tane eş kareden meydana gelmiştir.
\( m(\hat{ BAC}) = \alpha \)  ise \( \cot \alpha \) nın değeri nedir?

 

 

\[
\text{A) } \frac{1}{3} \quad
\text{B) } 3 \quad
\text{C) } \frac{11}{7} \quad
\text{D) } \frac{7}{11} \quad
\text{E) } 4
\]

 

Çözüm:

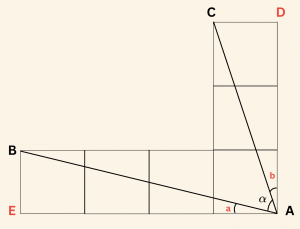
\( m(\hat {CAD}) = b  \) ve  \( m ( \hat { EAB } ) = a \) ise  \( \alpha = 90^\circ  \;-\;  (a + b) \)  olur.

Eş karelerin kenarlarını 1 birim seçelim.

 

 

 

Şekil üzerindeki oranlar:

\[\begin{aligned} AE = 1 \text{ birim} \\ \\
AB = 1 \text{ birim} \\ \\
BE = 1 \text{ birim} \\ \\
BC = 1 \text{ birim} \\ \\
AC = \text{(bağlantı uzunluğu)}   \end{aligned}\]

cotangent değerini bulmak için,

\[ \cot \alpha = \frac{\text{komşu kenar}}{\text{karşı kenar}} \]  oranı hesaplanır.

CDA dik üçgeninden \[ \quad \tan b = \frac{|CD|}{|DA|} = \frac{1}{3} \]

BEA dik üçgeninden \[ \tan a = \frac{|BE|}{|EA|} = \frac{1}{4} \text{ tür.} \]

O halde,

\[
\cot \alpha = \cot [90^\circ – (a + b)] = \tan (a + b)
\]

\[\begin{aligned}\tan (a + b) = \frac{\tan a + \tan b}{1 – \tan a \cdot \tan b} \\ \\ = \frac{\frac{1}{4} + \frac{1}{3}}{1 – \frac{1}{4} \cdot \frac{1}{3}}  \\ \\ = \frac{\frac{7}{12}}{1 – \frac{1}{12}} \\ \\  = \frac{\frac{7}{12}}{\frac{11}{12}} \\ \\ = \frac{7}{11} \text{ dir.} \end{aligned}\]

\(\textbf{Cevab: D} \)

 

SORU 12

 

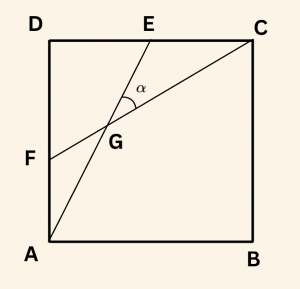
Yandaki şekilde ABCD karedir.
\( m( \hat{ EGC}) = \alpha \)
\( |DE| = |DF| = |FA|  \) ise  \( \sin \alpha \) nın değeri nedir?

 

 

 

\[
\text{A) } \frac{3}{4} \quad
\text{B) } \frac{3}{5} \quad
\text{C) } \frac{2}{3} \quad
\text{D) } \frac{2}{\sqrt{5}} \quad
\text{E) } \frac{3}{\sqrt{5}}
\]

Çözüm:

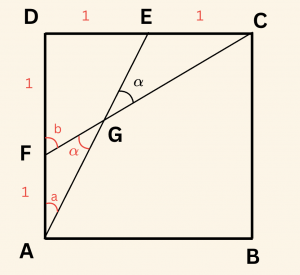\( m (\hat {DAE} ) = a \)  ve \(  m(\hat { DFC} ) = b \)  olsun.

\( b = a + \alpha \)    ise    \( \alpha = b \;- \; a \)  olur.

\( |DE| = |DF| = |FA| = 1  \) birim seçilirse,

\( |DC| = |DA| = 2  \) birim olur.

Önce \(\tan \alpha\) nın değerini bulalım.

ADE dik üçgeninden:

\[
\tan a = \frac{|DE|}{|DA|} = \frac{1}{2}
\]

CDF dik üçgeninden:

\[
\tan b = \frac{|DC|}{|DF|} = \frac{2}{1} = 2
\]

O halde:

\[\begin{aligned}\tan \alpha = \tan (b \; – \; a) &= \frac{\tan b \; – \; \tan a}{1 + \tan b \cdot \tan a}\\ \\  &= \frac{2 \; – \; \frac{1}{2}}{1 + 2 \cdot \frac{1}{2}} \\ \\  &= \frac{\frac{3}{2}}{2} \\ \\  &= \frac{3}{4} \end{aligned}\]

Dik üçgenden \(\sin \alpha\) nın değerini bulalım.

\[
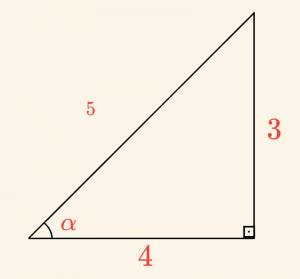
\sin \alpha = \frac{3}{5}
\]

bulunur

 

\(\textbf{Cevab: B} \)

 

SORU 13

 

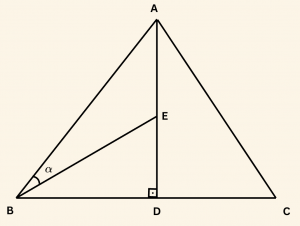
Yandaki ABC eşkenar üçgeninde,
\( m(\hat{ ABE} ) = \alpha\),
\( |AE| = |ED| \) ,
\(  [BC] \perp [AD]  \) ise,
\( \tan \alpha \)  nın değeri nedir?

 

\[
\text{A) } \frac{\sqrt{3}}{2} \quad
\text{B) } \frac{\sqrt{3}}{3} \quad
\text{C) } \frac{\sqrt{3}}{4} \quad
\text{D) } \frac{\sqrt{3}}{5} \quad
\text{E) } \frac{\sqrt{3}}{6}
\]

Çözüm:

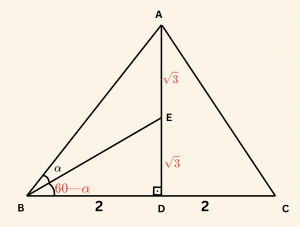
\( |BC| = 4 \)  birim seçilirse,
\( [AD] \) yüksekliği, kenar ortay olduğundan,

\[
|BD| = |DC| = 2 \text{ birim}
\]
\[
|AD| = \frac{4 \sqrt{3}}{2} = 2 \sqrt{3} \text{ birim,}
\]
\[
|AE| = |ED| = \sqrt{3} \text{ birim olur.}
\]

\( m(\hat{ ABC}) = 60^\circ \) ve \(  m(\hat{ ABE}) = \alpha \) olduğundan,

\( m(\hat{ EBD) } = 60^\circ \;-\; \alpha \) dır.

O halde, BDE dik üçgeninden:

\[
\tan (60^\circ – \alpha) = \frac{|ED|}{|BD|} = \frac{\sqrt{3}}{2}
\]

Ayrıca:

\[
\tan (60^\circ – \alpha) = \frac{\tan 60^\circ – \tan \alpha}{1 + \tan 60^\circ \tan \alpha}
\]

Eşitlik yazılırsa:

\[
\frac{\tan 60^\circ – \tan \alpha}{1 + \tan 60^\circ \tan \alpha} = \frac{\sqrt{3}}{2}
\]

\[
\frac{\sqrt{3} – \tan \alpha}{1 + \sqrt{3} \tan \alpha} = \frac{\sqrt{3}}{2}
\]

Çapraz çarpım yapalım:

\[
2 (\sqrt{3} – \tan \alpha) = \sqrt{3} (1 + \sqrt{3} \tan \alpha)
\]

Dağıtalım:

\[
2 \sqrt{3} – 2 \tan \alpha = \sqrt{3} + 3 \tan \alpha
\]

\[
2 \sqrt{3} – \sqrt{3} = 3 \tan \alpha + 2 \tan \alpha
\]

\[
\sqrt{3} = 5 \tan \alpha \Rightarrow \tan \alpha = \frac{\sqrt{3}}{5}
\]

\(\textbf{Cevab: D} \)

 

SORU 14

 

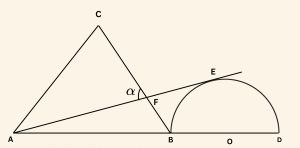
Yandaki şekilde O merkezli yarım çemberle ABC eşkenar üçgeni verilmiştir.
\( m(\hat{ CFA}) = \alpha, \quad |AB| = |BD|, \)
\(AE, E \)  noktasında yarım çembere teğettir.

Buna göre, \( \tan \alpha \)nın değeri nedir?

\[
\text{A) } \frac{1 + \sqrt{3}}{3} \quad
\text{B) } \frac{2 + \sqrt{3}}{3} \quad
\text{C) } \frac{2 – \sqrt{3}}{3} \quad
\text{D) } \frac{\sqrt{3}}{4} \quad
\text{E) } \frac{\sqrt{2} + 4 \sqrt{3}}{4 – \sqrt{6}}
\]

Çözüm:

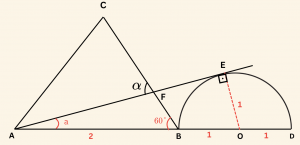E değme noktasından çizilen dikme merkezden geçer.
\( |AB| = |BD| = 2  \)  birim seçilirse,
\( |OB| = |OE| = 1 \)  birim ve AE0 dik üçgeninde Pisagor bağıntısından:

\[
|AE| = 2 \sqrt{2} \text{ birim olur.}
\]

\( m(\hat{ FAB})  =  a \) denilirse  \( m(\hat{ CBA}) = 60^\circ \) olduğundan
\(\alpha = a + 60^\circ  \) olur.

O halde, AEO dik üçgeninden:

\[
\tan a = \frac{|OE|}{|AE|} = \frac{1}{2 \sqrt{2}} = \frac{\sqrt{2}}{4}
\]

\[
\tan \alpha = \tan (a + 60^\circ) = \frac{ \tan a + \tan 60°}{1\;- \; \tan a \cdot \tan 60° }
\]

\[ = \frac{\sqrt{2 }/4 + \sqrt{3 } }{1 \;- \; \sqrt{ 2 }/ 4 \cdot \sqrt{3 } } \]
\[ = \frac{ \sqrt{ 2 } + 4 \sqrt{3 }}{4 \;- \; \sqrt{ 6 } } \]

\(\textbf{Cevab: E} \)

 

SORU 15

 

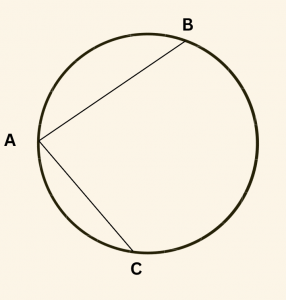
Yandaki şekilde yarıçap uzunluğu R birim olan bir çember verilmiştir.
\[
|AB| = \frac{2\sqrt{5} R}{5}, \quad |AC| = \frac{6R}{5} \text{ olduğuna göre, } \tan (\hat{ BAC}) \text{ in değeri nedir?}
\]

 

\[
\text{A) } -2 \quad \text{B) } -1 \quad \text{C) } 2 \quad \text{D) } 3 \quad \text{E) } 4
\]

 

Çözüm:

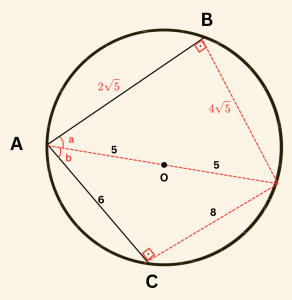\(R = 5 \) birim seçilirse çap uzunluğu \( |AA’| = 10 \) birim, \( |AB| = 2\sqrt{5} \) birim ve \( |AC| = 6 \) birim olur.

\( [BA’]  \) ve \( [CA’] \)  çizildiğinde B ve C çapı gören çevre açıları olduğundan:
\[
m(\hat{ B}) = m(\hat{ C}) = 90^\circ \text{ olur.}
\]

ABA’ dik üçgeninde Pisagor bağıntısından:
\[
|BA’| = 4 \sqrt{5} \text{ birim,}
\]

ACA’ dik üçgeninde Pisagor bağıntısından:
\[
|CA’| = 8 \text{ birimdir.}
\]

\( m(\hat{ BAA’}) = a,  m(\hat { A’AC} ) = b \) diyelim.

ABA’ dik üçgeninden:
\[
\tan a = \frac{|BA’|}{|AB|} = \frac{4 \sqrt{5}}{2 \sqrt{5}} = 2
\]

ACA’ dik üçgeninden:
\[
\tan b = \frac{|CA’|}{|AC|} = \frac{8}{6} = \frac{4}{3}
\]

O halde:
\[
\tan (\hat{ BAC}) = \tan (a + b) = \frac{\tan a + \tan b}{1 – \tan a \cdot   \tan b} = \frac{2 + \frac{4}{3}}{1 – 2 \cdot \frac{4}{3}}
\]

\[
= \frac{\frac{10}{3}}{1 – \frac{8}{3}} = \frac{\frac{10}{3}}{-\frac{5}{3}} = -2
\]

\(\textbf{Cevab: A} \)

 

SORU 16

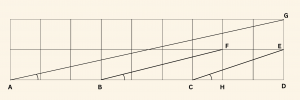
Yukarıdaki 18 eş kareden meydana gelen şekilde

\( m(\hat{ DAG}) = a, \quad m(\hat{ DBF} ) = b, \quad m(\hat { DCE}) = c \)  ise,

\( a + b + c \) nin ölçüsü kaç derecedir?

\[
\text{A) } 30^\circ \quad \text{B) } 45^\circ \quad \text{C) } 60^\circ \quad \text{D) } 75^\circ \quad \text{E) } 90^\circ
\]

Çözüm:

GDA dik üçgeninden:
\[
\tan a = \frac{|GD|}{|AD|} = \frac{2}{9}
\]

FHB dik üçgeninden:
\[
\tan b = \frac{|FH|}{|BH|} = \frac{1}{4}
\]

EDC dik üçgeninden:
\[
\tan c = \frac{|ED|}{|CD|} = \frac{1}{3}
\]

Önce:
\[
\tan (a + b) = \frac{\tan a + \tan b}{1 – \tan a \cdot   \tan b} = \frac{\frac{2}{9} + \frac{1}{4}}{1 – \frac{2}{9} \cdot \frac{1}{4}} = \frac{\frac{17}{36}}{1 – \frac{2}{36}} = \frac{\frac{17}{36}}{\frac{34}{36}} = \frac{1}{2}
\]

Son olarak:
\[
\tan [(a + b) + c] = \frac{\tan (a + b) + \tan c}{1 – \tan (a + b) \cdot \tan c} = \frac{\frac{1}{2} + \frac{1}{3}}{1 – \frac{1}{2} \cdot \frac{1}{3}} = \frac{\frac{5}{6}}{\frac{5}{6}} = 1
\]

Dolayısıyla:
\[
a + b + c = 45^\circ
\]

\(\textbf{Cevab: B } \)