Yarım Açı Formülleri
\( \bullet \quad \text{sin}(a + b) = \sin a . \cos b + \sin b . \cos a \) formülünde b yerine a yazılırsa,
\[
1) \quad \ \sin 2a = 2 \sin a \cos a
\]
\( \bullet \quad \text{cos}(a + b) = \cos a \cos b – \sin a \sin b \) formülünde b yerine } a yazılırsa,
\[
2) \quad \ \cos 2a = \cos^2 a – \sin^2 a
\]
\( \bullet \quad cos^2 a = 1 – \sin^2 a \) ve \( \sin^2 a = 1 – \cos^2 a \) olduğundan,
\[
\cos 2a = 1 – 2 \sin^2 a
\]
veya \[
\cos 2a = 2 \cos^2 a – 1 \]
Buradan,
\[
\sin^2 a = \frac{1 – \cos 2a}{2}
\]
\[ \cos^2 a = \frac{1 + \cos 2a}{2} \]
\[
\tan (a + b) = \frac{\tan a + \tan b}{1 – \tan a \tan b}
\]
formülünde \( b \) yerine \( a \) yazılırsa,
\[
3) \quad \ \tan 2a = \frac{2 \tan a}{1 – \tan^2 a}
\]
\[
\cot (a + b) = \frac{\cot a \cot b – 1}{\cot a + \cot b}
\]
formülünde \( b \) yerine \( a \) yazılırsa,
\[
4) \quad \cot 2a = \frac{\cot^2 a \; – \; 1}{2 \cot a}
\]
\[
2 \tan \frac{x}{2} = \frac{2 \tan \frac{x}{2}}{1 – \tan^2 \frac{x}{2}}
\]
\[ \tan x = \frac{2 \tan (x/2) }{1 \; – \; \tan^2 {x/2}} \]
formülünde \(\tan \frac{x}{2} = u\) denilirse.
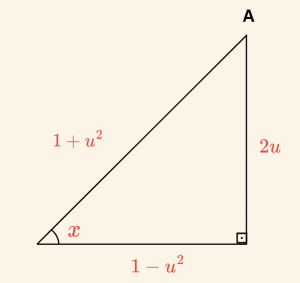
\[ \tan x = \frac{2u}{1- u^2} \]
\[\sin x = \frac{2u}{1+ u^2} \]
\[ \sin x = \frac{2 \tan x/2}{1 + \tan^2 x/2} \quad \text{ve } \quad \cos x = \frac{1- \tan^2 x/2 }{1 + \tan^2 x/2} \]
elde edilir.
Yukarıda ki denklemleri tablo olarak göstermek gerekirse
\[
\begin{array}{| l | }
\hline \\
1) \quad \sin 2a = 2 \sin a \cos a \\ \\
\hline \\
2) \quad \cos 2a = \cos^2 a – \sin^2 a \\ \\
\hline \\
3) \quad \tan 2a = \Large \frac{2 \tan a}{1 – \tan^2 a} \\ \\
\hline \\
4) \quad \cot 2a = \Large \frac{\cot^2 a \; – \; 1}{2 \cot a} \\ \\
\hline
\end{array}
\]
Örnekler:
\( \bullet \quad \sin x = 2 \sin \frac{x}{2} \cos \frac{x}{2} \)
\( \bullet \quad \cos 24^\circ = \cos^2 12^\circ – \sin^2 12^\circ = 1 – 2 \sin^2 12^\circ \)
\( \bullet \quad \tan 4x = \frac{2 \tan 2x}{1 – \tan^2 2x} \)
\( \bullet \quad \sin \frac{\pi}{4} = 2 \sin \frac{\pi}{8} \cdot \cos \frac{\pi}{8} \)
Örnek:
\( \sin 15^\circ \) ile \( \tan 22.5^\circ \) yi hesaplayalım.
\(
\bullet \quad \sin^2 a = \frac{1 – \cos 2a}{2} \) \[ \Rightarrow \sin^2 15^\circ = \frac{1 – \cos 30^\circ}{2}
\]
\[
\Rightarrow \sin^2 15^\circ = \frac{1 – \frac{\sqrt{3}}{2}}{2} = \frac{1 – \frac{\sqrt{3}}{2}}{2}
\]
\[
\Rightarrow \sin 15^\circ = \frac{\sqrt{6} – \sqrt{2}}{4}
\]
\(\bullet \quad \tan 2a = \frac{2 \tan a}{1 – \tan^2 a} \)
\[
\Rightarrow \tan 45^\circ = \frac{2 \tan 22.5^\circ}{1 – \tan^2 22.5^\circ} = 1
\]
\[
1 – \tan^2 22.5^\circ = 2 \tan 22.5^\circ
\]
\[
\Rightarrow \tan^2 22.5^\circ + 2 \tan 22.5^\circ – 1 = 0
\]
\(
\tan 22.5^\circ = t \text{ denilirse,}
\)
\[
t^2 + 2t – 1 = 0
\]
\[
\Rightarrow t = \tan 22.5^\circ = \sqrt{2} – 1 \text{ dir.}
\]
Örnek:
\[
\sin 18^\circ \text{ değerini bulalım.}
\]
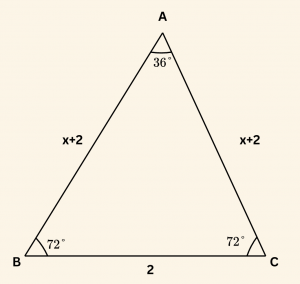
\( m(\hat{ A}) = 36^\circ \) ve \( |BC| = 2 \) birim olacak şekilde ABC ikizkenar üçgeni çizelim.
\[ |AB| = |AC| > |BC| \text{ olacağından,} \]
\[|AB| = |AC| = x + 2 \text{ birim olsun.} \]
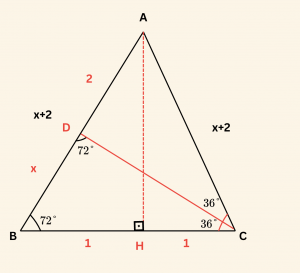
C açısının açıortayı \( [DC] \) çizilirse,
\[ m(\hat{ CDB} ) = 72^\circ, \quad |BC| = |DC| = 2 \text{ birim}, \quad |AD| = |CD| = 2 \text{ birim} \]
ve |BD| = x birim olur.
\[
\triangle CAB \sim \triangle BCD \text{ olduğundan:}
\]
\[
\frac{|CB|}{|BD|} = \frac{|CA|}{|BC|}
\]
\[
\frac{2}{x} = \frac{x+2}{2}
\]
\[
\Rightarrow x^2 + 2x – 4 = 0 \Rightarrow x = \sqrt{5} – 1 \text{ olur.}
\]
AHC dik üçgeninden:
\[
\cos (\hat{ ACB} ) = \frac{|HC|}{|AC|} \Rightarrow \cos 72^\circ = \frac{1}{\sqrt{5} – 1 + 2}
\]
Sonuç olarak:
\[
\cos 72^\circ = \sin 18^\circ = \frac{\sqrt{5} – 1}{4}
\]
SORU 17
\[
\frac{\sin 33^\circ}{\sin 11^\circ} \;- \; \frac{\cos 33^\circ}{\cos 11^\circ} \text{ ifadesinin değeri kaçtır?}
\]
\[
\text{A) } 3 \quad \text{B) } 2 \quad \text{C) } 1 \quad \text{D) } -1 \quad \text{E) } -2
\]
Çözüm:
\[
\frac{\sin 33^\circ}{\sin 11^\circ}\; -\; \frac{\cos 33^\circ}{\cos 11^\circ} = \frac{\sin 33^\circ \cdot \cos 11^\circ\; -\; \sin 11^\circ \cdot \cos 33^\circ}{\sin 11^\circ \cdot \cos 11^\circ}
\]
\[
= \frac{\sin(33^\circ \;- \;11^\circ)}{\sin 11^\circ \cdot \cos 11^\circ} = \frac{\sin 22^\circ}{\sin 11^\circ \cdot \cos 11^\circ}
\]
\[
= \frac{2 \sin 11^\circ \cdot \cos 11^\circ}{\sin 11^\circ \cdot \cos 11^\circ} = 2
\]
\(\textbf{Cevab: B} \)
SORU 18
\[
\cos^2 \frac{13\pi}{12} + \sin^2 \frac{5\pi}{12} \text{ ifadesinin değeri kaçtır?}
\]
\[
\text{A) } 1 \quad \text{B) } 2 \;- \;\sqrt{3} \quad \text{C) } 2 + \sqrt{3} \quad \text{D) } \frac{2 – \sqrt{3}}{2} \quad \text{E) } \frac{2 + \sqrt{3}}{2}
\]
Çözüm:
\[
\cos^2 \frac{13\pi}{12} + \sin^2 \frac{5\pi}{12} = \cos^2 \left( \pi + \frac{\pi}{12} \right) + \sin^2 \left( \frac{\pi}{2} \; – \; \frac{\pi}{12} \right)
\]
\[
= (-\cos \frac{\pi}{12})^2 + \cos^2 \frac{\pi}{12} = 2 \cos^2 \frac{\pi}{12}
\]
\[
2 \cos^2 a = 1 + \cos 2a \text{ olduğundan,}
\]
\[
= 1 + \cos \frac{2\pi}{12}
\]
\[ 1 + \frac{ \sqrt{ 3} }{2} = \frac{2 + \sqrt{ 3} }{2} \]
\(\textbf{Cevab: E} \)
SORU 19
\[
A = 1 + \tan 2x \cdot \tan 4x \quad \text{ ise } \quad \frac{1}{A}
\]
aşağıdakilerden hangisine eşittir?
\[
\text{A) } \cos 4x \quad \text{B) } \sin 4x \quad \text{C) } \sec 4x \quad \text{D) } \cos 2x \quad \text{E) } \sin 2x
\]
Çözüm:
\[
A = 1 + \tan 2x \cdot \tan 4x
\]
\[ = 1 + \frac{\sin 2x}{\cos 2x} \cdot \frac{\sin 4x}{\cos 4x} \]
\[ = 1 + \frac{\sin 2x}{\cos 2x} \cdot \frac{2 \sin 2x \cdot \cos 2x}{\cos^2 2x\; – \; \sin^2 2x} \]
\[
= 1 + \frac{2 \sin^2 2x}{\cos^2 2x \; – \; \sin^2 2x}
\]
\[
= 1 + \frac{2 \sin^2 2x}{\cos 4x}
\]
\[
= \frac{\cos^2 2x – \sin^2 2x + 2 \sin^2 2x}{\cos^2 2x \;- \;\sin^2 2x}
\]
\[ = \frac{\cos^2 2x + \sin^2 2x}{\cos 4x} = \frac{1}{\cos 4x} \]
\[
\frac{1}{A} = \cos 4x
\]
SORU 20
\[
\pi < x < 2\pi \text{ olmak üzere } A = \frac{1 – \cos x}{1 + \cos x} \text{ ise, } \sqrt{A} \text{ aşağıdakilerden hangisine eşittir?}
\]
\[
\text{A) } -1 \quad \text{B) } \tan \frac{x}{2} \quad \text{C) } – \tan \frac{x}{2} \quad \text{D) } 2 \tan \frac{x}{2} \quad \text{E) } -2 \tan \frac{x}{2}
\]
Çözüm:
\[
A = \frac{1 – \cos x}{1 + \cos x}
\]
\[ = \frac{1 – (1 – 2 \sin^2 \frac{x}{2})}{1 + (-1 + 2 \cos^2 \frac{x}{2})} \]
\[ = \frac{2 \sin^2 \frac{x}{2}}{2 \cos^2 \frac{x}{2}} = \tan^2 \frac{x}{2} \]
\[
\Rightarrow \sqrt{A} = \sqrt{\tan^2 \frac{x}{2}} = \left| \tan \frac{x}{2} \right|
\]
\[
\pi < x < 2\pi \Rightarrow \frac{\pi}{2} < \frac{x}{2} < \pi \text{ için } \to \tan \frac{x}{2} < 0
\]
\[
\sqrt{A} = – \tan \frac{x}{2}
\]
\(\textbf{Cevab: C} \)
SORU 21
\[ \cos 40^\circ = a \] ise, \( \cos 280^\circ \) nin a cinsinden eşiti aşağıdakilerden hangisidir?
\[
\text{A) } 1 – a \quad \text{B) } 1 – 2a \quad \text{C) } 1 – a^2 \quad \text{D) } -1 + 2a^2 \quad \text{E) } 1 – 2a^2
\]
Çözüm:
\[
\cos 280^\circ = \cos(270^\circ + 10^\circ) = \sin 10^\circ = \cos 80^\circ
\]
\[
\cos 80^\circ = -1 + 2 \cos^2 40^\circ = -1 + 2a^2
\]
\(\textbf{Cevab: D} \)
SORU 22
\[
1 \;- \; 2 \sin^2 x + \frac{\sin^2 2x \; – \; 2 \cos^2 x}{\cos^4 x \;- \;\sin^4 x}
\]
ifadesinin eşiti aşağıdakilerden hangisidir?
\[
\text{A) } – \tan 2x \quad \text{B) } \tan 2x \quad \text{C) } – \cot 2x \quad \text{D) } 1 \quad \text{E) } -1
\]
Çözüm:
\[
1 – 2 \sin^2 x + \frac{\sin^2 2x \;- \; 2 \cos^2 x}{\cos^4 x \;-\; \sin^4 x}
\]
\[
= \cos 2x + \frac{\sin^2 2x \;- \; 2 \cos^2 x}{(\cos^2 x + \sin^2 x)(\cos^2 x \; – \; \sin^2 x)}
\]
\[
= \cos 2x + \frac{\sin^2 2x \;- \;2 \cos^2 x}{1 \cdot \cos 2x}
\]
\[
= \cos 2x + \frac{\sin^2 2x \; – \;2 \cos^2 x}{\cos 2x}
\]
\[
= \frac{\cos^2 2x + \sin^2 2x \; – \;2 \cos^2 x}{\cos 2x}
\]
\[
= \frac{1 \;-\; 2 \cos^2 x}{\cos^2 x} = \frac{- (-1 + 2 \cos^2 x)}{-1+ 2\cos^2x} = -1
\]
\(\textbf{Cevab: E} \)
SORU 23
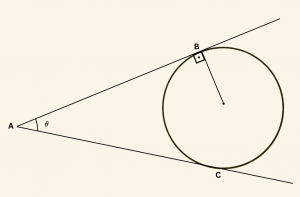Yandaki şekilde O merkezli çembere A noktasından çizilen teğetlerin değme noktaları B ve C’dir.
\( 3|OB| = |AB|\) ve \( \hat { BAC} = \theta\) ise, \( \sin \theta \) değeri nedir?
\[
\text{A) } \frac{1}{5} \quad \text{B) } \frac{2}{5} \quad \text{C) } \frac{3}{5} \quad \text{D) } \frac{4}{5} \quad \text{E) } \frac{2}{3}
\]
Çözüm:
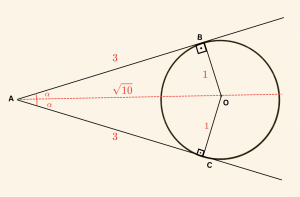
[AO] çizilirse, \( m(\hat{ BAO}) = m(\hat{ CAO} ) = \alpha\) ve \( \theta = 2 \alpha \) olur.
\( |OB| = 1 \) birim seçilirse, \( |AB| = 3\) birim olur.
ABO dik üçgeninde Pisagor bağıntısından:
\[
|AO| = \sqrt{1^2 + 3^2} = \sqrt{10} \text{ birim olur.}
\]
O halde, ABO dik üçgeninden:
\[
\sin \alpha = \frac{|OB|}{|AO|} = \frac{1}{\sqrt{10}}
\]
\[
\sin \theta = \sin 2 \alpha = 2 \sin \alpha \cos \alpha
\]
\[
= 2 \cdot \frac{1}{\sqrt{10}} \cdot \frac{3}{\sqrt{10}} = \frac{6}{10} = \frac{3}{5}
\]
\(\textbf{Cevab: C } \)
SORU 24
\[
\frac{\pi}{2} < x < \pi \quad \text{ olmak üzere,}
\]
\[
\frac{\sin^2 x}{1 + \cos^2 x + \cos 2x} = \frac{4}{3}
\]
olduğuna göre, \( \tan 2x \) in değeri nedir?
\[
\text{A)} -\frac{1}{3} \quad
\text{B)} -\frac{1}{2} \quad
\text{C)} 2 \quad
\text{D)} \frac{4}{3} \quad
\text{}{E)} \frac{3}{4}
\]
Çözüm:
\[
\frac{\sin^2 x}{1 + \cos^2 x + \cos 2x} = \frac{4}{3}
\]
\[
\Rightarrow \frac{\sin^2 x}{1 + \cos^2 x + (-1 + 2 \cos^2 x)} = \frac{4}{3}
\]
\[
\Rightarrow \frac{\sin^2 x}{3 \cos^2 x} = \frac{4}{3} \Rightarrow \tan^2 x = 4
\]
\[
\frac{\pi}{2} < x < \pi \text{ olduğundan,}
\]
\[
\tan x = -2 \text{ olur. O halde,}
\]
\[
\tan 2x = \frac{2 \tan x}{1 – \tan^2 x} = \frac{2 \cdot (-2)}{1 – (-2)^2} = \frac{4}{3} \text{ tür.}
\]
\(\textbf{Cevab: D} \)
SORU 25
\[
\frac{\cos 2x – 3 \sin x + 1}{2 + \sin x} = -\frac{1}{5} \text{ olduğuna göre,}
\]
\(\cot 2x \) kaça eşittir?
\[
\text{A) } \frac{24}{7} \quad \text{B) } \frac{7}{24} \quad \text{C) } \frac{4}{3} \quad \text{D) } \frac{3}{4} \quad \text{E) } 1
\]
Çözüm:
\[
\frac{\cos 2x \;- \;3 \sin x + 1}{2 + \sin x} = -\frac{1}{5}
\]
\[
\Rightarrow \frac{1 \;- \; 2 \sin^2 x \;-\; 3 \sin x + 1}{2 + \sin x} = -\frac{1}{5}
\]
\[
\Rightarrow -\frac{2 \sin^2 x + 3 \sin x – 2}{2 + \sin x} = -\frac{1}{5}
\]
\[
\Rightarrow \frac{(\sin x + 2)(2 \sin x \; – \; 1)}{2 + \sin x} = \frac{1}{5}
\]
\[
\Rightarrow 2 \sin x \;-\; 1 = \frac{1}{5} \Rightarrow \sin x = \frac{3}{5}
\]
\[
\text{O halde, } \tan x = \frac{3}{4}
\]
\[
\tan 2x = \frac{2 \tan x}{1 \;- \;\tan^2 x} = \large{ \frac{2 \cdot \frac{3}{4}}{1 – \left( \frac{3}{4} \right)^2 }} = \frac{24}{7}
\]
\[
\cot 2x = \frac{1}{\tan 2x} = \frac{7}{24} \text{ tür.}
\]
\(\textbf{Cevab: B} \)
SORU 26
\[ \tan \left( \frac{\pi}{4} \;- \; x \right) – \cot \left( x \; – \; \frac{\pi}{4} \right) \]s işleminin sonucu aşağıdakilerden hangisidir?}
\[
\text{A) } 1 \quad \text{B) } -1 \quad \text{C) } 2 \quad \text{D) } -2 \sec 2x \quad \text{E) } 2 \sec 2x
\]
Çözüm:
\[
\tan \left( \frac{\pi}{4} \; – \; x \right) – \cot \left( x \;- \; \frac{\pi}{4} \right)
\]
\( \star \quad – \cot \theta = \cot (- \theta) \) olduğundan,
\[
= \tan \left( \frac{\pi}{4} \;- \; x \right) + \cot \left( \frac{\pi}{4}\; – \; x \right)
\]
\[
= \large { \frac{\sin \left( \frac{\pi}{4} \;- \;x \right)}{\cos \left( \frac{\pi}{4} \; – \; x \right)} + \frac{\cos \left( \frac{\pi}{4} \;-\; x \right)}{\sin \left( \frac{\pi}{4}\; – \; x \right)} }
\]
\[ \large {=
\frac{ \sin^2 \left( \frac{\pi}{4} \;- \;x \right) + \cos^2 \left( \frac{\pi}{4} \;- \; x \right) }{ \cos \left( \frac{\pi}{4} \; – \;x \right) \cdot \sin \left( \frac{\pi}{4}\; – \;x \right) } }
\]
\[
= \large{ \frac{1}{\frac{1}{2} \sin \left( \frac{\pi}{2} – 2x \right)} } \quad (\sin \theta \cdot \cos \theta = \frac{1}{2} \sin 2 \theta)
\]
\[
= \frac{2}{\cos 2x} = 2 \sec 2x \text{ tir.}
\]
\(\textbf{Cevab: E} \)
SORU 27
\(180^\circ < x < 270^\circ \) olmak üzere, \( \large \tan x = \frac{3}{4} \) ise \( \large \sin \frac{x}{2} \) nin değeri nedir?
\[
\text{A)} \frac{3}{\sqrt{10}} \quad \text{B)} -\frac{3}{\sqrt{10}} \quad \text{C)} \frac{1}{\sqrt{10}} \quad \text{D)} -\frac{1}{\sqrt{10}} \quad \text{E)} \frac{3}{4}
\]
Çözüm:
\[\tan x = \large{ \frac{2 \tan \frac{x}{2}}{1 – \tan^2 \frac{x}{2}} } \]
\[\Rightarrow \frac{3}{4} = \frac{2 \tan \frac{x}{2}}{1 – \tan^2 \frac{x}{2}}\]
\[
\Rightarrow 3 – 3 \tan^2 \frac{x}{2} = 8 \tan \frac{x}{2}
\]
\[
\Rightarrow 3 \tan^2 \frac{x}{2} + 8 \tan \frac{x}{2} – 3 = 0
\]
\[
\tan \frac{x}{2} = t \text{ denilirse,}
\]
\[
3t^2 + 8t – 3 = 0
\]
\[
\Rightarrow t = -3 \text{ veya } t = \frac{1}{3} \text{ olur.}
\]
\[
180^\circ < x < 270^\circ \Rightarrow 90^\circ < \frac{x}{2} < 135^\circ \text{ olduğundan}
\]
\[
\Rightarrow \tan \frac{x}{2} = -3 \text{ tür. O halde,}
\]
\[
\frac{x}{2} \text{ dar açı kabul edilerek } |\tan \frac{x}{2}| = 3 \text{ bulunur.}
\]
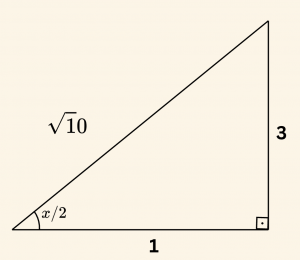Yandaki dik üçgenden,
\[ \left | \sin \frac{x}{2} \right | = \frac{ 3}{ \sqrt{10 } } \]
\[ 90° < \frac{x}{2} < 135° \quad \text{için} \]
\[ \sin \frac{x}{2} > 0 \quad \text{olduğundan } \quad \sin \frac{x}{2} = \frac{ 3}{ \sqrt{10 } } \]
\(\textbf{Cevab: A} \)
Uyarı:
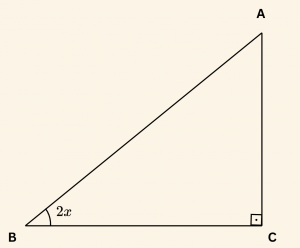\( 2x \) dar açı olmak şartıyla, \( 2x \) in trigonometrik oranlarından birisi belli iken \( x \) in trigonometrik oranları, aşağıdaki dik üçgen yardımıyla bulunabilir.
\(2x \) in verilen trigonometrik oranına uygun bir şekilde ABC dik üçgeni çizilir.
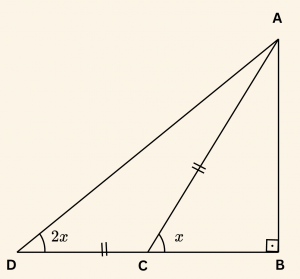
Daha sonra \( [AC] \) ye eşit uzunlukta, \( [BC] \) nin uzantısı olan \( [DC] \) çizilir.
D noktasının A köşesiyle birleştirilmesiyle ABD dik üçgeni elde edilir. Elde edilen bu dik üçgende D açısının ölçüsü \( x \) olur.
SORU 28
\( 0^\circ < x < 45^\circ \) olmak üzere,
\[ \cos x = \frac{2 \sqrt{2}}{\sqrt{13}} + \sin x \] ise \( \cot x \) in değeri kaçtır?
\[
\text{A )} 2 \quad \text{B )} 3 \quad \text{C )} 4 \quad \text{D )} 5 \quad \text{E )} 6
\]
Çözüm:
\[
\cos x = \frac{2 \sqrt{2}}{\sqrt{13}} + \sin x \Rightarrow \cos x – \sin x = \frac{2 \sqrt{2}}{\sqrt{13}}
\]
\[
\text{eşitliğin her iki tarafının karesi alınırsa,}
\]
\[
\cos^2 x + \sin^2 x – 2 \cos x \sin x = \frac{8}{13}
\]
\[
\Rightarrow 1 – \sin 2x = \frac{8}{13}
\]
\[
\Rightarrow \sin 2x = \frac{5}{13} \text{ olur. O halde,}
\]
\[
\text{Aşağıdaki ABD dik üçgeninden}
\]
\[
\cot x = \frac{|BD|}{|AB|} = \frac{25}{5} = 5 \text{ tir.}
\]
\(\textbf{Cevab: D} \)
SORU 29
\[
\text{Bir ABC üçgeninde } \tan A = 2 \text{ ve } \tan B = \frac{2}{3} \text{ ise, } \tan \frac{C}{2} \text{ nin değeri nedir?}
\]
\[
\text{A)} \frac{4}{3} \quad \text{B)} \frac{3}{4} \quad \text{C)} \frac{8}{\sqrt{65}} \quad \text{D)} \frac{\sqrt{65}}{8} \quad \text{E)} \frac{8}{1+\sqrt{65}}
\]
Çözüm:
\[
A + B + C = 180^\circ \Rightarrow A + B = 180^\circ – C
\]
\[
\Rightarrow \tan (A + B) = \tan (180^\circ – C) = – \tan C
\]
\[
\Rightarrow \frac{\tan A + \tan B}{1 – \tan A \tan B} = – \tan C
\]
\[
\Rightarrow \large{ \frac{2 + \frac{2}{3}}{1 – 2 \cdot \frac{2}{3}} } = – \tan C
\]
\[
\Rightarrow \large{ \frac{\frac{8}{3}}{-\frac{1}{3}} = – \tan C \Rightarrow \tan C} = 8
\]
\[
\text{FED dik üçgeninden}
\]
\[
\tan \frac{C}{2} = \frac{|FE|}{|ED|} = \frac{8}{1 + \sqrt{65}} \text{ tir.}
\]
\(\textbf{Cevab: E} \)