Bir Eşitsizlik Sisteminin Grafiği
Bir eşitsizlik sistemini meydana getiren eşitsizliklerin hepsini aynı anda sağlayan noktalar kümesinin analitik düzlemdeki görüntüsüne bu eşitsizlik sisteminin grafiği denir.
Eşitsizlik sisteminin grafiğini çizmek için sistemi meydana getiren eşitsizliklerin grafiği çizilir.
Bu grafiklerin kesiştikleri noktalar, eşitsizlik sisteminin grafiğidir.
Örnek:
\[
\left.
\begin{aligned}
y \geq x^2 + 1\\
\\
y + x^2 – 4 < 0\\
\end{aligned}
\right\} \Rightarrow \quad \text{eşitsizlik sisteminin grafiğini çizelim.}
\]
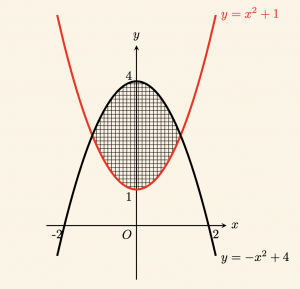
\[
\left.
\begin{aligned}
y \geq x^2 + 1 \\
\\
y +x^2 – 4 < 0\\
\end{aligned}
\right\} \Rightarrow \left. \begin{aligned} y \geq x^2 + 1 \\ \\ y < -x^2 + 4 \\ \end{aligned} \right\}
\]
Örnek:
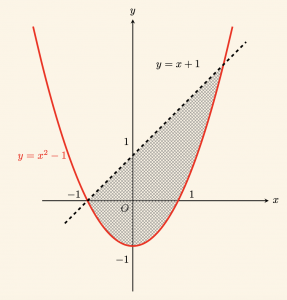
\[
\left.
\begin{aligned}
y \geq x^2 – 1\\
\\
y < x + 1 \\
\end{aligned}
\right\} \Rightarrow \quad \text{eşitsizlik sisteminin grafiğini çizelim.}
\]
Uyarı:
\( f(x) < y < g(x) \) eşitsizlik sisteminin grafiği, \( y = f(x) \) ve \( y = g(x) \) eğrileri (veya doğruları) arasındaki bölgedir.
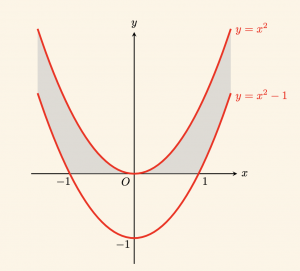
Örnek:
\[
\left.
\begin{aligned}
x^2 – 1 ≤ y ≤ x^2 \\
\\
y ≥ 0 \\
\end{aligned}
\right\} \Rightarrow \quad \text{eşitsizlik sisteminin grafiğini çizelim.}
\]
Bu sistem:
\(\bullet \) \(\quad y \geq 0 \) olan bölgeyi kısıtlar, yani sadece üst yarı düzlem,
\(\bullet \quad \) Alt sınırı \( y = x^2 – 1 \), üst sınırı \( y = x^2 \) olan aralıktır.
Yani, taralı alan:
\[
x^2 – 1 \leq y \leq x^2 \quad \text{ve} \quad y \geq 0
\]
koşulunu sağlayan bölgedir.
Parabolik bant bölgesi, sadece \( y \geq 0 \) kısmında gösterilir.
← Önceki Sayfa | Sonraki Sayfa →