Eşitsizlik Grafikleri
Bir eşitsizliği sağlayan noktalar kümesinin analitik düzlemdeki görüntüsüne bu eşitsizliğin grafiği denir.
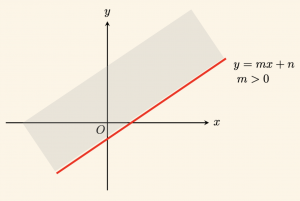
1) Şekildeki taralı bölge, \[ y \geq mx + n \quad m > 0 \quad \text{eşitsizliğinin grafiğidir. } \]
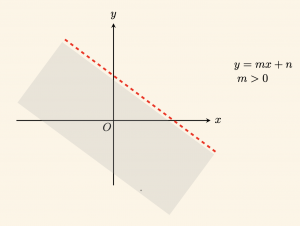
2) Şekildeki taralı düzlem \( y < mx + n \) eşitsizliğinin grafiğidir. Burada eşitlik olmadığından \( y = mx + n \) doğrusu üzerindeki noktalar eşitsizliği sağlamaz.
Bu yüzden \( y = mx + n \) doğrusu kesikli çizgiyle çizilir.
Parabol eşitsizlik grafikleri:
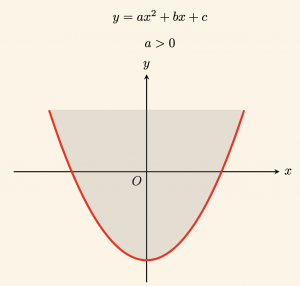
1) Şekildeki taralı düzlem \( y \geq ax^2 + bx + c \) eşitsizliğinin grafiğidir. (\(a > 0\))
2) Şekildeki taralı düzlem \( y > ax^2 + bx + c \) eşitsizliğinin grafiğidir. Burada eşitlik olmadığından \( y = ax^2 + bx + c \) parabolü üzerindeki noktalar eşitsizliği sağlamaz.
Bu yüzden parabol kesikli çizgiyle çizilir.
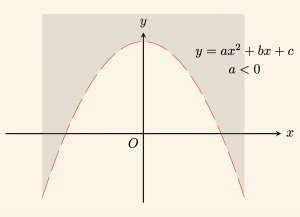
3) Şekildeki taralı düzlem \( y \leq ax^2 + bx + c \) eşitsizliğinin grafiğidir.
(\(a > 0\))
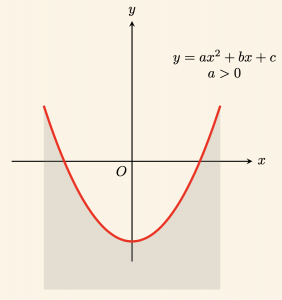
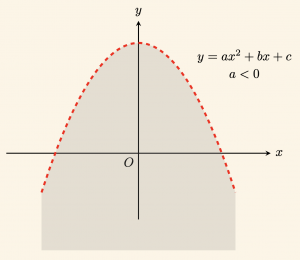
4) Şekildeki taralı düzlem \( y < ax^2 + bx + c \) eşitsizliğinin grafiğidir. Burada eşitlik olmadığından parabol kesikli çizgiyle çizilmiştir.
(\(a < 0\))
Uyarı:
\(y = f(x)\) eğrisi (veya doğrusu), analitik düzlemi iki bölgeye ayırır. Bu bölgelerden biri \(y > f(x)\), diğeri de \(y < f(x)\) eşitsizliğinin grafiğidir.
Bölgelerin birinden seçilen herhangi bir nokta, \(y = f(x)\) denkleminde yerine yazılarak
bu bölgeyi veren eşitsizliğin yönü belirlenir.
Örnek:
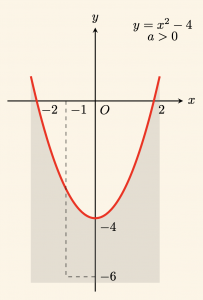
Yandaki şekilde grafiği verilen eşitsizliği bulalım.
Grafik üzerinde seçilen \(A(-1, -6)\) noktasının koordinatlarını \(y = x^2 – 4\) denkleminde yerine yazalım:
\[
x = -1 \quad \text{ ve } \quad y = -6 \;\; \text{ için:} \quad -6 < (-1)^2 – 4 \Rightarrow -6 < -3
\]
Olduğundan \( y \leq x^2 – 4 \) olarak bulunur.
Örnek:
\( y – x^2 + 4x \leq 0 \) eşitsizliğinin grafiğini çizelim.
Önce
\[
y – x^2 + 4x = 0 \Rightarrow y = x^2 – 4x
\]
parabolünü çizelim.
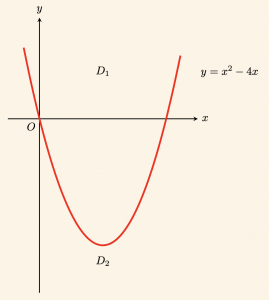
Parabol düzlemi \(D_1\) ve \(D_2\) olmak üzere iki düzleme ayırır. \(D_2\) düzlemi içinden seçilen \(A(0,\ -5)\) noktasının koordinatlarının eşitsizliği sağlayıp sağlamadığına bakalım:
\[
x = 0,\quad y = -5 \quad \text{ için } \quad y \; – \; x^2 + 4x \leq 0 \]
\[\Rightarrow -5 – \;0^2 + 4 \cdot 0 \leq 0 \Rightarrow -5 \leq 0
\]
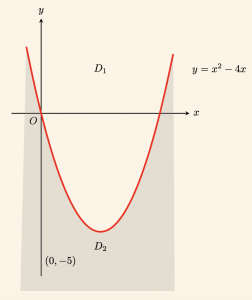
olduğundan, \(A(0,\ -5)\) noktasının içinde bulunduğu \(D_2\) düzlemi aranan bölgedir.
Örnek:
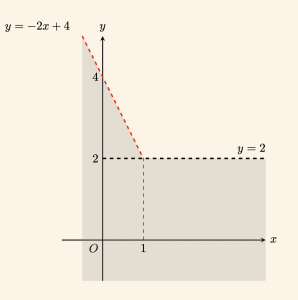
\( y < |x – 1| – x + 3 \) eşitsizliğinin grafiğini çizelim.
\(x \geq 1\) için:
\[|x – 1| = x – 1\] olduğundan,
\[
y < x – 1 – x + 3 \Rightarrow y < 2 \text{ olur.}
\]
\( x < 1 \) için:
\[|x – 1| = -(x – 1) = -x + 1\] olduğundan,
\[
y < -x + 1 – x + 3 \Rightarrow y < -2x + 4 \text{ olur.}
\]
Örnek:
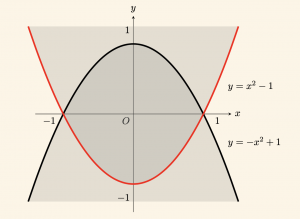
\( |y| \geq x^2 – 1 \) eşitsizliğinin grafiğini çizelim.
\(y \geq 0\) için: \(|y| = y\) olduğundan,
\[
y \geq x^2 – 1
\]
\(y < 0\) için: \(|y| = -y\) olduğundan,
\[
-y \geq x^2 – 1 \Rightarrow y \leq -x^2 + 1 \;\; \text{olur }
\]
Örnek:
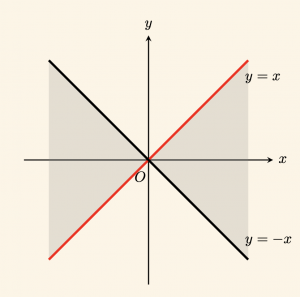
\( |y| \leq |x| \) eşitsizliğinin grafiğini çizelim.
\(x \geq 0 \) ve \(y \geq 0 \) için: \( |y| \leq |x| \Rightarrow y \leq x \)
\(x ≤ 0 \) ve \(y \geq 0 \) için: \( |y| \leq |x| \Rightarrow y \leq -x \)
\(x ≤ 0 \) ve \(y ≤ 0 \) için: \( |y| \leq |x| \Rightarrow -y \leq -x \Rightarrow y≥ x \)
\(x \geq 0 \) ve \(y ≤ 0 \) için: \( |y| \leq |x| \Rightarrow- y \leq x \Rightarrow y \geq -x\)
← Önceki Sayfa | Sonraki Sayfa →