Eşitsizlik Sistemi
Aynı anda sağlanan birden fazla eşitsizliğin oluşturduğu sisteme bir eşitsizlik sistemi denir. Sistemi meydana getiren eşitsizliklerin çözüm kümelerinin kesişimine de eşitsizlik sisteminin çözüm kümesi denir.
O halde eşitsizlik sisteminin çözüm kümesini bulmak için, eşitsizlik sistemini meydana getiren eşitsizliklerin çözüm kümeleri bulunarak kesişimleri alınır.
Örnek:
\[f(x) = x^3 + x^2 – x – 1 \geq 0 \]
\[ g(x) = \frac{x + 1}{-x^2 + 3x – 2} > 0 \]
eşitsizlik sisteminin çözüm kümesini bulalım.
\[ x^3 + x^2 – x – 1 = 0 \Rightarrow (x + 1)^2(x – 1) = 0 \]
\[ \Rightarrow x_1 = x_2 = -1 \text{ veya } x_3 = 1 \]
\[x + 1 = 0 \Rightarrow x = -1 \]
\[- x^2 + 3x – 2 = 0 \Rightarrow x_1 = 1 \text{ veya } x_2 = 2 \]
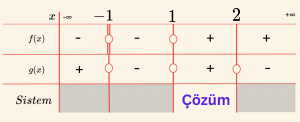
\[ \mathcal{Ç} = \{ x \mid 1 < x < 2, \, x \in \mathbb{R} \} \text{ olarak bulunur.} \]
SORU 14
\[ f(x) = \frac{x^2 \;- \; x^3}{x^2 + 2} \leq 0 \]
\[ g(x) = \frac{2}{x + 1} > 0 \]
eşitsizlik sistemini sağlayan aralıklardan birisi aşağıdakilerden hangisidir?
\[ \text{A) } x \geq 1 \quad
\text{B) } x < -1 \quad
\text{C) } x < 0 \quad
\text{D) } -1 < x < 0 \quad
\text{E) } 0 < x < 1 \]
Çözüm:
\[\begin{aligned} & x^2 \; – \; x^3 = 0 \Rightarrow x^2(1 – x) = 0 \Rightarrow x_1 = x_2 = 0 \text{ veya } x_3 = 1\\ \\
& x^2 + 2 = 0 \Rightarrow x^2 = -2 < 0 \text{ olduğundan reel kök yoktur.} \\ \\
&x + 1 = 0 \Rightarrow x = -1 \end{aligned}\]
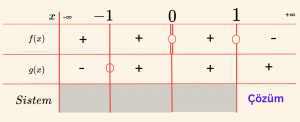
\[ \mathcal{Ç} = \{ x \mid 1 \leq x < \infty, \, x \in \mathbb{R} \} \cup \{ 0 \} \text{ dir.} \]
\(\textbf{Cevab: A} \)
SORU 15
\[ \frac{x^2 – x + 6}{x + 2} < x + 1 \leq \frac{3}{x – 1} \] eşitsizlik sistemini sağlayan aralıklardan biri aşağıdakilerden hangisidir?
\[ \text{A) } -3 < x < 0 \quad
\text{B) } x > 1 \quad
\text{C) } 0 < x \leq 2 \quad
\text{D) } -2 < x < 1 \quad
\text{E) } x < -2 \]
Çözüm:
\[ \frac{x^2 – x + 6}{x + 2} < x + 1 \quad \text{ve} \quad x + 1 \leq \frac{3}{x – 1} \]
\[ \Rightarrow f(x) = \frac{-4x + 4}{x + 2} < 0 \]
\[ \Rightarrow -4x + 4 = 0 \Rightarrow x = 1 \quad , \quad x + 2 = 0 \Rightarrow x = -2 \]
\[g(x) = \frac{x^2 – 4}{x – 1} \leq 0 \Rightarrow x^2 – 4 = 0 \Rightarrow x = \pm 2 \quad , \quad x – 1 = 0 \Rightarrow x = 1 \]
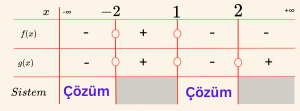
\[ \mathcal{Ç} = \{ x \mid x < -2 \text{ veya } 1 < x \leq 2, \, x \in \mathbb{R} \} \]
\(\textbf{Cevab: E} \)
SORU 16
\[ -1 < \frac{x^2 – 5}{x – 1} < 2 \] eşitsizlik sistemini aşağıdaki aralıklardan hangisi sağlar?
\[ \text{A) } x < -3 \quad
\text{B) } -1 < x < 1 \quad
\text{C) } 2 < x < 3 \quad
\text{D) } 1 < x < 2 \quad
\text{E) } x > 3 \]
Çözüm:
\[ -1 < \frac{x^2 – 5}{x – 1} < 2 \]
\[ -1 < \frac{x^2 \; – \; 5}{x- 1 } \quad \text{ve } \quad \frac{x^2-5}{x-1} < 2 \]
\[ \Rightarrow f(x) = \frac{x^2 + x – 6 }{x-1 } > 0 \Rightarrow x_1 = -3, \; x_2 = 2 \]
\[x^2 + x – 6= 0 \Rightarrow x_1= -3 \quad \text{veya } \quad x_2= 2 \]
\[\Rightarrow g(x) = \frac{x^2 -2x – 3 }{x-1 } <0 \Rightarrow x_1 = -1, \quad x_2 = 3 \]
\[x^2 -2x-3 =0 \Rightarrow x_1= -1 \quad \text{veya } \quad x_2= 3 \]
\[\Rightarrow x-1 =0 \Rightarrow x= 1 \]
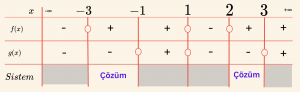
\[ \mathcal{Ç} = \{ x \mid -3 < x < -1 \quad \text{ veya } \quad 2 < x < 3, \; x \in \mathbb{R} \} \]
\(\textbf{Cevab: C} \)
SORU 17
\[ \frac{-x^2 + 2x – 3}{x^2 + 1} < x^2 + x + 1 < \frac{7}{x – 1} \] eşitsizlik sistemini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } x < 1 \quad
\text{B) } -3 < x < -1 \quad
\text{C) } -1 < x < 1 \quad
\text{D) } 1 < x < 2 \quad
\text{E) } x > 2 \]
Çözüm:
\[ \frac{-x^2 + 2x – 3}{x^2 + 1} < x^2 + x + 1 \quad \text{ve} \quad x^2 + x + 1 < \frac{7}{x – 1} \]
Burada \( \forall x \in \mathbb{R} \) için:
\[ – x^2 + 2x – 3 < 0, \quad x^2 + 1 > 0, \quad x^2 + x + 1 > 0 \text{ olduğundan} \]
\[ \frac{-x^2 + 2x – 3}{x^2 + 1} < x^2 + x + 1 \] eşitsizliğinin çözüm kümesi \( \mathcal{C}_1 = \mathbb{R} \) dir.
\[ x^2 + x + 1 < \frac{7}{x – 1} \Rightarrow x^2 + x + 1 – \frac{7}{x – 1} < 0 \]
\[ \Rightarrow \frac{x^3 – 8}{x – 1} < 0 \Rightarrow f(x) = \frac{x^3 – 8}{x – 1} < 0 \]
\[x^3 -8 =0 \Rightarrow x = 2 \quad \text{ve } \quad x-1 =0 \Rightarrow x= 1 \]
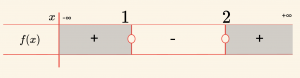
\[ Ç_2 = \{x | 1 < x < 2, \in \mathbb{R} \} \]
ve
\[ Ç = Ç_1 \cap Ç_2 = \{x | 1 < x < 2, \in \mathbb{R} \} \text{ dir.} \]
\(\textbf{Cevab: D} \)
← Önceki Sayfa | Sonraki Sayfa →