İkinci Dereceden Bir Bilinmeyenli Eşitsizlikler
\(a, b, c \in \mathbb{R} \) ve \( a \ne 0 \) olmak üzere,
\[ax^2 + bx + c > 0 \]
\[ ax^2 + bx + c \ge 0 \]
\[ ax^2 + bx + c < 0 \]
veya
\[ ax^2 + bx + c \le 0 \]
şeklindeki eşitsizliklere ikinci dereceden bir bilinmeyenli eşitsizlikler denir. İkinci dereceden bir bilinmeyenli bir eşitsizliği çözmek demek,
\[
f(x) = ax^2 + bx + c\]
üç terimlisinin işaretini inceleyerek eşitsizliği sağlayan aralığı bulmak demektir.
\[
f(x) = ax^2 + bx + c
\]
nin grafiğini çizerek işaretini inceleyelim.
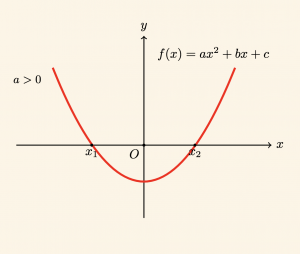
1) \( \quad \Delta > 0 \) olmak üzere
\[x < x_1 \quad \text{ veya } \quad x > x_2 \quad \text{ için } \quad f(x) > 0 \]
\[ x_1 < x < x_2 \quad \text{ için }\quad f(x) < 0 \;\; \text{dır.} \]
\[x < x_1 \quad \text{ veya } \quad x > x_2 \quad \text{ için } \quad f(x) < 0 \]
\[ x_1 < x < x_2 \quad \text{ için }\quad f(x) > 0 \;\; \text{dır.} \]
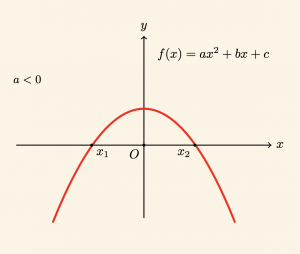
Buna göre,
\[
x < x_1 \;\; \text{ veya } \;\; x > x_2 \quad \text{ için } \;\; f(x) = ax^2 + bx + c \text{ ifadesinin işareti } a \text{ nın işaretiyle aynıdır,}
\]
\[
x_1 < x < x_2 \;\; \text{ için } \;\; f(x) = ax^2 + bx + c \;\; \text{ ifadesinin işareti } a \text{ nın işaretinin tersidir.}
\]
Bu durumu tabloda gösterelim.
\[
\begin{array}{|c | l | c r | r | r | }
\hline
x & -\infty & x_1 && & x_2 & +\infty \\
\hline
f(x)=ax^2+bx+c \;\; (\Delta > 0 ) & \text{a’nın işaretinin aynısı} & \circ\ &&\text{işaretinin tersi} & \circ& \text{işaretinin aynısı} \\
\hline
\end{array}
\]
Örnek:
\(f(x) = -x^2 + 7x – 6 \) üç terimlisinin işaretini inceleyelim.
\[
-x^2 + 7x – 6 = 0
\;\; \Longrightarrow \;\;
x_1 = 1 \quad \text{ veya } \quad x_2 = 6
\quad\text{ve}\quad
a = -1 < 0
\]
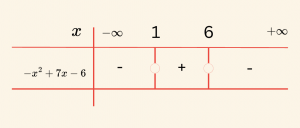
\[ \text{ Buna göre } \quad x < 1 \quad \text{veya} \quad x > 6 \quad \text{için} f(x) < 0 \]
\[ 1 < x < 6 \quad \text{için} \quad f(x) > 0 \]
Örnek:
\( m \in \mathbb{R} \) olmak üzere,
\( (m^2 + 1)x^2 + m^2 x – 1 < 0 \) eşitsizliğinin çözüm kümesini bulalım.
\[ (m^2 + 1)x^2 + m^2 x – 1 =0 \]
\[
\Rightarrow \bigl[(m^2 + 1)x – 1\bigr](x + 1) = 0
\quad\Longrightarrow\quad
x_1 = \frac{1}{m^2 + 1}, \quad x_2 = -1.
\]
\[
a = m^2 + 1 > 0 \quad (\text{parabol yukarı doğru açılır}).
\]
\[
\text{Parabol }(m^2+1)x^2 + m^2 x – 1 \text{ eksenleri }x = -1 \text{ ve }x = \frac{1}{m^2+1}\text{ de keser.}
\]
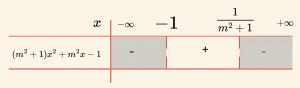
\[
\text{Çözüm kümesi: }
\{x| -1 < x < \frac{1}{m^2 + 1} \,x \in \mathbb{R} \}
\]
Örnek:
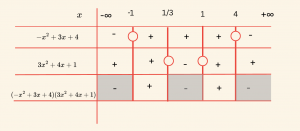
\(-x^2 + 3x + 4)(3x^2 – 4x + 1) > 0 \) eşitsizliğinin çözüm kümesini bulalım.
\[
-x^2 + 3x + 4 = 0 \Rightarrow x_1 = -1 \quad \text{ve} \quad x_2 = 4 \quad (a = -1 < 0)
\]
\[
3x^2 – 4x + 1 = 0 \Rightarrow x_1 = \frac{1}{3} \quad \text{ve} \quad x_2 = 1 \quad (a = 3 > 0)
\]
\[
\text{Kritik noktalar: } -1,\quad \frac{1}{3},\quad 1,\quad 4
\]
\[
\text{Eşitsizlik } > 0 \text{ olduğuna göre, işaretin pozitif olduğu aralıklar alınır.}
\]
\[
\text{Buna göre çözüm kümesi: } \quad \mathcal{Ç} = \left\{ x \in \mathbb{R} \;\middle|\; -1 < x < \frac{1}{3} \;\text{veya}\; 1 < x < 4 \right\}
\]
Uyarı:
Eşitsizliğin paydasını sıfır yapan değerler çözüm kümesinin elemanı olamayacağımdan çözüm kümesine alınmazlar. Eşitsizliğin payını sıfır yapan değerler ise sadece eşitlik olduğu durumlarda çözüm kümesine alınırlar.
Örnek:
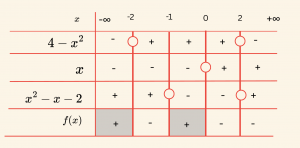
\[ f(x) = \frac{(4 \;- x^2)x}{x^2 \;- x \;- 2} < 0 \] eşitsizliğinin çözüm kümesini bulalım.
\[4 – x^2 = 0 \Rightarrow x = \pm2 \quad (a = -1 < 0) \]
\[x = 0 \quad (a = 1 > 0) \]
\[x^2 – x – 2 = 0 \Rightarrow x_1 = -1, \; \; x_2 = 2 \quad (a = 1 > 0) \]
\[
\text{Kritik noktalar: } -2, \; -1, \;0, \; 2
\]
\[
\text{f(x) < 0 olduğu yerler: } -2 < x < -1 \quad \text{ve} \quad x > 0 \quad \text{(2 hariç)}
\]
\[
\text{Çözüm kümesi:} \quad
\mathcal{Ç} = \left\{ x \;\middle|\; -2 < x < -1 \;\text{veya}\; x > 0, x \in \mathbb{R} \right\} \;- \; \{2\}
\]
Örnek:
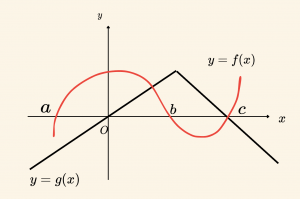
Yukarıdaki şekle göre \[\frac{f(x)}{g(x)} \geq 0 \] eşitsizliğinin çözüm kümesini bulalım.
\[f(x) = 0 \Rightarrow x = a, \quad x = b, \quad x = c \]
\[g(x) = 0 \Rightarrow x = 0, \quad x = c \]
\[
\text{İstenen: } \frac{f(x)}{g(x)} \geq 0 \Rightarrow \text{Pozitif veya sıfır olduğu bölgeler:}
\]
\[
x \in (-\infty, a] \cup (0, b]
\]
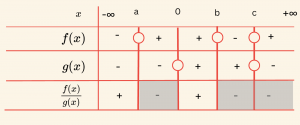
\[Ç = \left\{ x \in \mathbb{R} \;\middle|\; -\infty < x \leq a \; \text{veya} \; 0 < x \leq b \right\} \quad \text{olarak bulunur.} \]
2) \( \quad \Delta = 0 \) olmak üzere
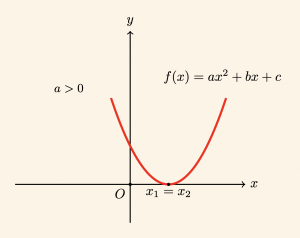
\[ x \neq -\frac{b}{2a} \;\; \text{için } \quad f(x) > 0 \;\; \text{dır.} \]
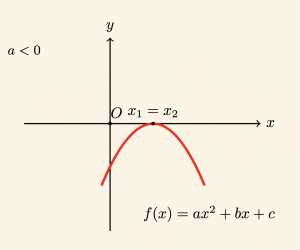
\[ x \neq -\frac{b}{2a} \;\; \text{için }, \quad f(x) < 0 \;\; \text{dır.} \]
\[
\text{Buna göre,} \quad x = -\frac{b}{2a} \quad \text{ için } f(x) = 0,
\]
\[
x \ne -\frac{b}{2a} \text{ için } f(x) = ax^2 + bx + c \text{ ifadesinin işareti, } a\text{’nın işaretiyle aynıdır.}
\]
Bu durumu tabloda gösterelim:

Örnek:
\( -4x^2 + 24x \;- 36 \) üç terimlisinin işaretini inceleyelim.
\[
-4x^2 + 24x \; – 36 = 0 \Rightarrow x_1 = x_2 = 3 \quad \text{ve} \quad a = -4 < 0 \quad \text{olduğundan }
\]
Bu durumda işaret tablosu:

\[ x \neq 3 \quad \text{için } \quad -4x^2 + 24x \; – 36 < 0 \;\; \text{dır. } \]
Örnek:
\( m \in \mathbb{R} \) olmak üzere, \( x^2 – 2mx – 2x + m^2 + 2m + 1 \) ifadesinin işaretini inceleyelim.
\[
x^2 – 2(m+1)x + (m+1)^2 = \left(x – (m+1)\right)^2 = 0 \]
\[\Rightarrow x_1 = x_2 = m+1 \]
\[
a = 1 > 0 \text{ olduğundan, işaret tablosu:}
\]

Sonuç \( x \ne m+1 \) için \( (x \;-\; (m+1))^2 > 0 \) olur.
3) \( \quad \Delta < 0 \) olmak üzere
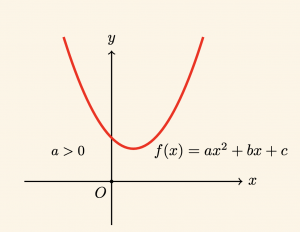
\[ \forall x \in \mathbb{R} \text{ için } f(x) > 0 \text{ dır.} \]
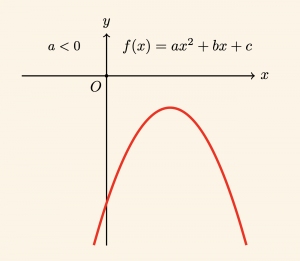
\[ \forall x \in \mathbb{R} \text{ için } f(x) < 0 \text{ dır.} \]
Buna göre \( f(x) = ax^2+bx+ c \) nin işareti a nın işaretinin aynısıdır. Bu durumu tabloda gösterelim.

Örnek:
\( f(x) = -x^2 + 3x- 3 \) üç terimlisinin işaretini inceleyelim.
\( -x^2 + 3x- 3 = 0 \Rightarrow \Delta = -3 < 0 \) ve \( a = -1 < 0 \) olduğundan

\(\forall \; x \in \mathbb{R} \) için \( f(x) = -x^2 + 3x\; – \; 3 < 0 \) dır.
Sonuç:
\( \Delta < 0 \) ve \( a > 0 \) ise, \( \forall x \in \mathbb{R} \) için (daima) \( f(x) = ax^2 + bx + c > 0, \)
\( \Delta < 0 \) ve \( a < 0 \) ise \( \forall x \in \mathbb{R} \) için (daima) \( f(x) = ax^2 + bx + c < 0 \) dır.
Örnek:
\( f(x) = x^2 \,- \; 2x + m \) üç terimlisi \( \forall x \in \mathbb{R} \) için \( -7 \) den büyük değerler aldığına göre, m hangi aralığın elemanıdır?
\[ \forall x \in \mathbb{R} \Rightarrow x^2 – 2x + m > -7 \]
\[
\Rightarrow x^2 – 2x + m + 7 > 0
\]
\[
a = 1 > 0 \quad \text{ve} \quad \Delta = (-2)^2 \;- \; 4 \cdot (m + 7) < 0
\]
\[
4 < 4 \cdot (m + 7) \Rightarrow 1 < m + 7 \Rightarrow m > -6 \;\; \text{olarak bulunur. }
\]
Örnek:
\( mx^2 + (2m + 1)x + m\; -\; 3 < 0 \) eşitsizliğinin daima doğru olması için m’nin değer kümesini bulalım.
\[
a = m < 0 \quad \text{ve} \quad \Delta = (2m + 1)^2 – 4m \cdot (m\; – \; 3) < 0
\]
\[
\Rightarrow 4m^2 + 4m + 1 \;- \; 4m^2 + 12m = 16m + 1 < 0 \]
\[\Rightarrow m < -\frac{1}{16}
\]
\[ m < -\frac{1}{16} \quad \text{için} \] \( m < 0 \) olduğundan
\[ \Rightarrow \mathcal{Ç} = \{ m \in \mathbb{R} \mid m < -\frac{1}{16} \}
\]
SORU 1
\( (m^2 + 1)x^2 + mx + 1 > 0 \) eşitsizliğinin daima doğru olması için m’nin alacağı değerler nedir?
\[\begin{aligned}
&\text{A) } \{ m | m m < 1, m \in \mathbb{R} \} \quad \\
&\text{B) } \{ m | m 1 < m < 4 , m \in \mathbb{R} \} \quad \\
&\text{C) } \{ m | > 4, m \in \mathbb{R} \} \quad \\
&\text{D) } \mathbb{R} \quad \\
&\text{E) } Ø \end{aligned}\]
Çözüm:
\( a = m^2 + 1 > 0 \) ve \( \Delta = m^2 – 4 \cdot (m^2 + 1) \cdot 1 < 0 \)
\[ \Rightarrow -3m^2\; -\; 4 < 0 \text{ olmalıdır.} \]
\[
\forall m \in \mathbb{R} \text{ için } m^2 + 1 > 0 \text{ ve } -3m^2 – 4 < 0 \text{ olduğundan } \mathcal{Ç} = \mathbb{R} \text{ olur.}
\]
\(\textbf{Cevab: D} \)
SORU 2
\( mx^2 + (2m – 2)x + m – 1 < 0 \) eşitsizliğinin daima doğru olması için \(m \) nin alacağı değerlerin kümesi aşağıdakilerden hangisidir?
\[\begin{aligned}
&\text{A) } \{ m \mid m > 2,\, m \in \mathbb{R} \} \quad \\
&\text{B) }\{ m \mid m < -2,\, m \in \mathbb{R} \} \quad \\
&\text{C) } \{ m \mid -2 < m < 2,\, m \in \mathbb{R} \} \quad \\
&\text{D) } \mathbb{R} \quad \\
&\text{E) } Ø \end{aligned}\]
Çözüm:
\[
a = m < 0 \quad \text{ve} \quad \Delta = (2m – 2)^2 – 4m(m – 1) < 0
\]
\[
\Rightarrow -4m + 4 < 0 \Rightarrow m > 1 \text{ olmalıdır.}
\]
\[
\text{Ancak } m < 0 \text{ ve } m > 1 \text{ aynı anda olamaz.}
\Rightarrow \mathcal{Ç} = Ø
\]
\(\textbf{Cevab: E} \)
SORU 3
Aşağıdaki şekle göre m için aşağıdakilerden hangisi doğrudur?
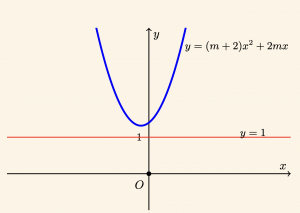
\[ \text{A) } m< 1 \quad \text{B) } 1 < m < 3 \quad \text{C) } 0 < m < 2 \quad \text{D) } m > 0 \quad \text{E) } m > 2 \]
Çözüm:
Verilen şekle göre \( y = (m + 2)x^2 + 2mx + m > 1 \) eşitsizliği daima doğru olmalıdır.
\[ (m + 2)x^2 + 2mx + m > 1 \]
\[\Rightarrow (m + 2)x^2 + 2mx + m – 1 > 0 \text{ olması için,} \]
\[ a = m + 2 > 0 \Rightarrow m > -2 \text{ ve} \]
\[ \Delta = 4m^2 – 4 \cdot (m + 2) \cdot (m – 1) < 0 \]
\[ \Rightarrow -4m + 8 < 0 \]
\[ \Rightarrow m > 2 \text{ olmalıdır.} \]
\[ m > 2 \text{ için } m > -2 \text{ olduğundan } m > 2 \text{ dir.} \]
\(\textbf{Cevab: E} \)
Pratik Yolla İşaret İnceleme:
A(x), B(x) \text{ ve } C(x) birer polinom olmak üzere,
\[ A(x) \cdot B(x) \cdot C(x) \] veya \[ \frac{A(x) \cdot B(x)}{C(x)} \] şeklindeki ifadelerin işaretini incelerken yapılması gereken işlemleri sıralayalım.
1) \( A(x) = 0, B(x) = 0 \) ve \( C(x) = 0 \) denklemlerinin reel kökleri bulunarak küçükten büyüğe doğru tabloya yerleştirilir.
Burada karşımıza çıkan köklerden birbirinin aynısı olanların adedi çift sayı ise bu kök çift katlı köktür.
2) \( A(x), B(x) \) ve \( C(x) \) polinomlarının en büyük dereceli terimlerinin katsayılarının işaretleri çarpılır. Elde edilen bu işaret, tabloda en büyük kökün sağına yazılır.
3) Tablo, sola doğru köklerde işaret değiştirerek devam eder. Fakat çift katlı köklerde işaret değiştirmez.
Uyarı:
\[ \frac{A(x) \cdot B(x)}{C(x)} \geq 0 \] veya \[ \frac{A(x) \cdot B(x)}{C(x)} \leq 0 \] şeklindeki eşitsizliklerde \( C(x) = 0 \) denkleminin kökleri çözüm kümesinin elemanı olamaz.
\( A(x) = 0 \) ve \( B(x) = 0 \) denklemlerinin kökleri çözüm kümesinin elemanıdır.
\[ \frac{A(x) \cdot B(x)}{C(x)} > 0 \quad \text{veya} \quad \frac{A(x) \cdot B(x)}{C(x)} < 0 \]
şeklindeki eşitsizliklerde \( A(x) = 0, \;\; B(x) = 0 \) ve \( C(x) = 0 \) denklemlerinin kökleri çözüm kümesinin elemanı olamaz.
Örnek:
\( – x^3 + 5x^2 – 6x \leq 0 \) eşitsizliğinin çözüm kümesini bulalım.
\( – x^3 + 5x^2 – 6x = 0 \Rightarrow x = 0 \) veya \( x = 2 \) veya \( x = 3 \) tür.
Polinomun en büyük dereceli terimi \( -x^3 \) ün katsayısının işareti \( (-) \) olduğundan en büyük kök olan 3’ün sağındaki işaret \( (-) \) dir.
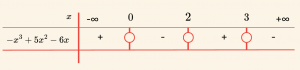
\[ \mathcal{Ç} = \{ x \mid 0 \leq x \leq 2 \quad \text{ veya } \quad 3 \leq x < +\infty, \, x \in \mathbb{R} \} \] olarak bulunur.
Örnek:
\( x^4 \; – \; x^3 \; – \; x + 1 > 0 \) eşitsizliğinin çözüm kümesini bulalım.
\[ x^4 \; – \; x^3 \; – \; x + 1 = 0 \Rightarrow (x^3 – 1)(x – 1) = 0 \Rightarrow (x^2 + x + 1)(x – 1)^2 = 0 \]
\[ x^2 + x + 1 = 0 \Rightarrow \Delta < 0 \text{ olduğundan denklemin reel kökü yoktur.} \]
\[ (x – 1)^2 = 0 \Rightarrow x_1 = x_2 = 1 \text{ çift katlı kök olduğundan tablo, 1’de işaret değiştirmez.} \]
Polinomun en büyük dereceli terimi \( (x^4) \) ün katsayısının işareti \( (+) \) olduğundan 1’in sağındaki işaret \( (+)\) dir.

\[ \mathcal{Ç} = \mathbb{R} – \{ 1 \} \text{ olarak bulunur.} \]
Örnek:
\[ f(x) = \frac{x^2 – 4}{-x^2 + 2x – 2} \geq 0 \] eşitsizliğinin çözüm kümesini bulalım.
\[\begin{aligned} &x^2 – 4 = 0 \Rightarrow x_1 = -2 \quad \text{ veya } \quad x_2 = 2 \\
\\
-& x^2 + 2x – 2 = 0 \Rightarrow \Delta < 0 \quad \text{ olduğundan reel kök yoktur.} \end{aligned} \]
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (x^2) \) ve \( (-x^2) \) nin katsayılarının işaretleri çarpımı \( (+) \cdot (-) = (-) \) dir.
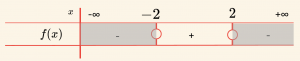
\[ \mathcal{Ç} = \{ x \mid -2 \leq x \leq 2 \} \]
Örnek:
\[ \frac{x}{2} \;-\; \frac{1}{2} < \frac{1}{x} \] eşitsizliğinin çözüm kümesini bulalım.
\[\frac{x}{2}\; -\; \frac{1}{2}\; – \; \frac{1}{x} < 0\]
\[ \frac{x \;-\; 1}{2} \; – \; \frac{1}{x} < 0 \Rightarrow \frac{x^2 \;- \;x \;- \; 2}{2x} < 0 \]
\[ x^2 \;-\; x \;-\; 2 = 0 \Rightarrow x_1 = -1, \, x_2 = 2 \]
\[ 2x = 0 \Rightarrow x = 0 \text{ dır.} \]
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (x^2) \) ve \( (x) \) in katsayılarının işaretleri çarpımı \( (+) \cdot (+) = (+) \) dir.
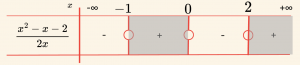
\[ \mathcal{Ç} = \{ x \mid -\infty < x < -1 \text{ veya } 0 < x < 2, \, x \in \mathbb{R} \} \]
Örnek:
\[ f(x) = \frac{(9 – x^2) \cdot x^4}{x^2 – 2x – 3} \geq 0 \] eşitsizliğinin çözüm kümesini bulalım.
\[
\begin{aligned}
&9 – x^2 = 0 \Rightarrow x_1 = -3, \, x_2 = 3 \\
\\
&x^4 = 0 \Rightarrow x_1 = x_2 = x_3 = x_4 = 0 \quad \text{ (çift katlı kök)} \\
\\
&x^2 \;-\; 2x \;-\; 3 = 0 \Rightarrow x_1 = -1,\quad x_2 = 3 \\
\\
\end{aligned}
\]
Burada, \( 3 \) de iki kez elde edildiğinden çift katlı köktür. Pay ve paydadaki polinomların en büyük dereceli terimleri \( (x^2), \, (x^4), \, (x^2) \) nin katsayılarının işaretleri çarpımı \( (-) \cdot (+) \cdot (+) = (-) \) dir.
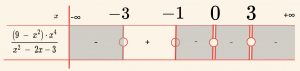
\[ \mathcal{Ç} = \{ x | -3 ≤ x ≤ -1 , \, x \in \mathbb{R} \} \cup \{0 \} \;\; \text{dır.} \]
SORU 4
\[ f(x) = \frac{-x^2 + 6x – 9}{(-x^2 + x – 2)(x^2 – 4)} \leq 0 \] eşitsizliğini sağlayan kaç tane \(x \) tamsayı değeri vardır?
\[ \text{A) } 2 \quad \text{B) } 3 \quad \text{C) } 4 \quad \text{D) } 5 \quad \text{E) } 6 \]
Çözüm:
\[- x^2 + 6x – 9 = 0 \Rightarrow -(x – 3)^2 = 0 \Rightarrow x_1 = x_2 = 3 \]
\[ – x^2 + x – 2 = 0 \text{ denkleminde } \Delta < 0 \text{ olduğundan reel kök yoktur.} \]
\[ x^2 – 4 = 0 \Rightarrow x_1 = -2 \text{ veya } x_2 = 2 \]
\Pay ve paydadaki polinomların en büyük dereceli terimleri \( (-x^2), (-x^2), (x^2) \) nin katsayılarının işaretleri çarpımı
\( (-) \cdot (-) \cdot (+) = (+) \) dır.
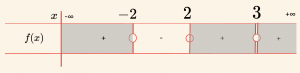
\[ \mathcal{Ç} = \{ x \mid -2 < x < 2, \, x \in \mathbb{R} \} \cup \{ 3 \} \text{ olduğundan} \]
\( x \) in alabileceği tamsayı değerleri \( -1, 0, 1 \) ve \( 3 \) olup dört tanedir.}
\(\textbf{Cevab: C} \)
SORU 5
\[ f(x) = \frac{(1 – x^3)^2 \cdot 2^x}{x^5 + 32} > 0 \] eşitsizliğini sağlayan x değerleri için aşağıdakilerden hangisi doğrudur?
\[\text{A) } x < -2 \quad
\text{B) } x < 1 \quad
\text{C) } x > 0 \quad
\text{D) } -2 < x < 1 \quad
\text{E) } x > -2 \]
Çözüm:
\[ (1 – x^3)^2 = 0 \Rightarrow x_1 = x_2 = 1 \]
\[\forall x \in \mathbb{R} \quad \text{ için } \quad 2^x > 0 \] olduğundan bu ifade \( f(x) \) in işaretini etkilemez.
\[ x^5 + 32 = 0 \Rightarrow x = -2 \]
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (x^6), (x^5) \) in katsayılarının işaretleri çarpımı \((+) \cdot (+) = (+) \) dir.
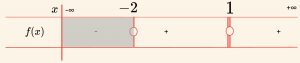
\[\mathcal{Ç} = \{ x \mid -2 < x < 1 \text{ veya } 1 < x < \infty, \, x \in \mathbb{R} \} \]
\(\textbf{Cevab: D} \)
SORU 6
\[ f(x) = \frac{-\frac{1}{x} +1 \;-\; x }{\sqrt{ x^2+4}-1 } < 0 \] eşitsizliğini sağlayan aralık aşağıdakilerden hangisidir?
\[\text{A) } x < -1 \quad
\text{B) } -1 < x < 0 \quad
\text{C) } x > 0 \quad
\text{D) } -2 < x < -1 \quad
\text{E) } -3 < x < -2 \]
Çözüm:
\[ f(x) = \frac{-\frac{1}{x} +1 \;-\; x }{\sqrt{ x^2+4}-1 } < 0 \Rightarrow \frac{-x^2 + x – 1}{x(\sqrt{x^2 + 4} \;- \;1)} < 0 \]
\(- x^2 + x – 1 = 0 \) denkleminde \( \Delta < 0 \) olduğundan reel kök yoktur.
\( \forall x \in \mathbb{R} \) için \( \sqrt{x^2 + 4}\; -\; 1 > 0 \) olduğundan bu ifade f(x) in işaretini etkilemez.
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (-x^2), (x) \) in katsayılarının işaretleri çarpımı \( (-) \cdot (+) = (-) \) dir.

\[ \mathcal{Ç} = \{ x \mid 0 < x < \infty, \, x \in \mathbb{R} \} \]
\(\textbf{Cevab: C} \)
SORU 7
\[ f(x) = \frac{(x^4 – 1)(1 – x^3)}{x^2 – 4x + 3} \leq 0 \] eşitsizliğini sağlayan aralıklardan biri aşağıdakilerden hangisidir?
\[ \text{A) } x \leq -1 \quad
\text{B) } -2 < x < 1 \quad
\text{C) } -1 \leq x < 3 \quad
\text{D) } 1 < x < 3 \quad
\text{E) } 1 \leq x < 1 \]
Çözüm:
\[ x^4 – 1 = 0 \Rightarrow x_1 = -1 \text{ veya } x_2 = 1 \]
\[ 1 – x^3 = 0 \Rightarrow x = 1 \]
\[ x^2 – 4x + 3 = 0 \Rightarrow x_1 = 1 \text{ veya } x_2 = 3 \]
Burada 1, üç kez elde edildiğinden çift katlı kök değildir. Pay ve paydadaki polinomların en büyük dereceli terimleri \( (x^4), (-x^3), (x^2) \) nin katsayılarının işaretleri çarpımı \( (+) \cdot (-) \cdot (+) = (-) \) dir.
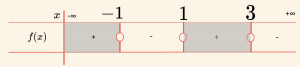
\[ \mathcal{Ç} = \{ x \mid -1 \leq x < 1 \text{ veya } x > 3, \, x \in \mathbb{R} \} \]
\(\textbf{Cevab: E} \)
SORU 8
\[ x + \frac{12}{x} > 6 + \frac{8}{x^2} \] eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } 1 < x < 3 \quad
\text{B) } -1 < x < 1 \quad
\text{C) } x < 0 \quad
\text{D) } 0 < x < 2 \quad
\text{E) } x > 2 \]
Çözüm:
\[ x + \frac{12}{x} > 6 + \frac{8}{x^2} \Rightarrow x + \frac{12}{x}\; – \; 6\; -\; \frac{8}{x^2} > 0 \]
\[\Rightarrow f(x) = \frac{x^3\; -\; 6x^2 + 12x\; -\; 8}{x^2} > 0 \]
\[ x^3 \;- \;6x^2 + 12x\; – \;8 = (x – 2)^3 = 0 \Rightarrow x_1 = x_2 = x_3 = 2 \]
\[ x^2 = 0 \Rightarrow x_1 = x_2 = 0 \]
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (x^3), (x^2) \) nin katsayılarının işaretleri \( (+) \cdot (+) = (+) \) dir.
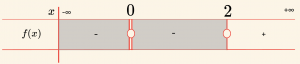
\[ \mathcal{Ç} = \{ x \mid x> 2 , \; x \in \mathbb{R} \} \]
\(\textbf{Cevab: E} \)
SORU 9
\( a < 0 < b \) olmak üzere,
[f(x) = \frac{x^2 – (a + b)x + ab}{(ax^2 – b)x^4} > 0 \] eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } a < x < 0 \quad
\text{B) } a < x < b \quad
\text{C) } x < a \quad
\text{D) } x > b \quad
\text{E) } x > 0 \]
Çözüm:
\[ x^2 – (a + b)x + ab = 0 \Rightarrow x_1 = a \text{ veya } x_2 = b \]
\[ ax^2 – b = 0 \Rightarrow x^2 = \frac{b}{a} < 0 \] olduğundan reel kök yoktur.
\[ x^4 = 0 \Rightarrow x_1 = x_2 = x_3 = x_4 = 0 \]
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (x^2), (ax^2), (x^4) \) ün katsayılarının işaretleri çarpımı
\( (+) \cdot (-) \cdot (+) = (-) \) dir.
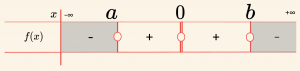
\[ \mathcal{Ç} = \{ x \mid a < x < b, \, x \in \mathbb{R} \}\; – \; \{ 0 \} \]
\(\textbf{Cevab: A} \)
SORU 10
\( m^2 + \frac{1}{m} < 0 \) olmak üzere,
\[f(x) = \frac{mx^2 + (1 – m^2)x – m}{x^2 – m^2} \geq 0 \] eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[ \text{A) } m < x < 0 \quad
\text{B) } x < m \quad
\text{C) } x > m \quad
\text{D) } -m < x \leq -\frac{1}{m} \quad
\text{E) } x \geq -\frac{1}{m} \]
Çözüm:
\[ m^2 + \frac{1}{m} < 0 \Rightarrow \frac{m^3 + 1}{m} < 0 \]
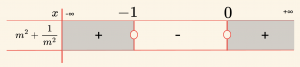
Buradan \( -1 < m < 0 \) bulunur. O halde,
\[ mx^2 + (1 – m^2)x – m = 0 \Rightarrow x_1 = m \text{ veya } x_2 = -\frac{1}{m} \]
\[ x^2 – m^2 = 0 \Rightarrow x_1 = m \text{ veya } x_2 = -m \]
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (mx^2), (x^2) \) nin katsayılarının işaretleri çarpımı
\( (-) \cdot (+) = (-) \) dir.
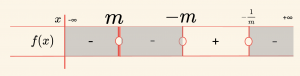
\[ \mathcal{Ç} = \{ x \mid -m < x \leq -\frac{1}{m}, \, x \in \mathbb{R} \} \]
\(\textbf{Cevab: D} \)
SORU 11
\[ f(x) = \frac{x + 5}{x^3 + 8} \;- \; \frac{x}{x^2\; – \;2x + 4} + \frac{1}{x + 2} \geq 0\] eşitsizliğini sağlayan kaç tane \( x \) tamsayı değeri vardır?
\[ \text{A) } 3 \quad
\text{B) } 4 \quad
\text{C) } 5 \quad
\text{D) } 6 \quad
\text{E) } 7 \]
Çözüm:
\[ f(x) = \frac{x + 5}{x^3 + 8}\; -\; \frac{x}{x^2 \;- \;2x + 4} + \frac{1}{x + 2} \geq 0 \]
Payda eşitlenirse,
\[ \Rightarrow f(x) = \frac{-3x + 9}{(x + 2)(x^2 – 2x + 4)} \geq 0 \] olur.
\[-3x + 9 = 0 \Rightarrow x = 3 \]
\[x + 2 = 0 \Rightarrow x = -2 \]
\[x^2 – 2x + 4 = 0 \text{ denkleminde } \Delta < 0 \] olduğundan reel kök yoktur.
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (-3x), \, (x), \, (x^2) \) nin katsayılarının işaretleri çarpımı \(
(-) \cdot (+) \cdot (+) = (-) \) dir.
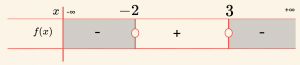
\[ \mathcal{Ç} = \{ x \mid -2 < x \leq 3, \, x \in \mathbb{R} \} \text{ olduğuna göre} \]
eşitsizliği sağlayan x tamsayı değerleri \( -1, \, 0, \, 1, \, 2, \, 3 \) olup beş tanedir.
\(\textbf{Cevab: C} \)
SORU 12
\[ f(x) = \frac{x^{1995} + 1}{(1 – x)^{1995}} > 0 \] eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } x < -1 \quad
\text{B) } -1 < x < 1 \quad
\text{C) } x > 1 \quad
\text{D) } x > 0 \quad
\text{E) } x < 0 \\ \]
Çözüm:
\[ x^{1995} + 1 = 0 \Rightarrow x = -1 \]
\[ (1 – x)^{1995} = 0 \Rightarrow x = 1 \]
Pay ve paydadaki polinomların en büyük dereceli terimleri \( (x^{1995}), \, (-x^{1995}) \) in katsayılarının işaretleri çarpımı \( (+) \cdot (-) = (-) \) dir.
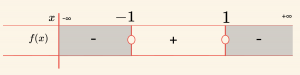
\[ \mathcal{Ç} = \{ x \mid -1 < x < 1, \, x \in \mathbb{R} \} \]
\(\textbf{Cevab: B} \)
SORU 13
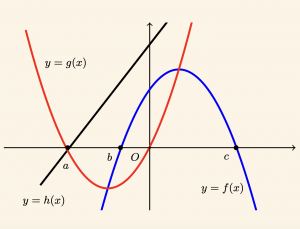
Yukarıdaki şekilde \( y = f(x) \) ve \( y = g(x) \) parabolleri ile \( y = h(x) \) doğrusu verilmiştir. Buna göre
\[ R(x) = \frac{g(x) \cdot h(x)}{f(x)} \geq 0 \] eşitsizliğini sağlayan aralıklardan biri aşağıdakilerden hangisidir?
\[ \text{A) } x > c \quad
\text{B) } b < x < 0 \quad
\text{C) } 0 \leq x < c \quad
\text{D) } x < 0 \quad
\text{E) } x > 0 \]
Çözüm:
\[ g(x) = 0 \Rightarrow x_1 = a \text{ veya } x_2 = 0 \]
\[ h(x) = 0 \Rightarrow x = a \]
\[ f(x) = 0 \Rightarrow x_1 = b \text{ veya } x_2 = c \]
\( g(x)\) polinomunun en büyük dereceli teriminin katsayısının işareti \( (+) \) dir. Çünkü parabolün kolları Oy ekseninin pozitif yönündedir.
\( h(x) \) polinomunun en büyük dereceli teriminin katsayısının işareti \( (+) \) dir. Çünkü doğrunun eğimi pozitiftir.
\( f(x) \) polinomunun en büyük dereceli teriminin katsayısının işareti \( (-) \) dir. Çünkü parabolün kolları Oy ekseninin negatif yönündedir.
O halde bu işaretlerin çarpımı \( (+) \cdot (+) \cdot (-) = (-) \) dir.
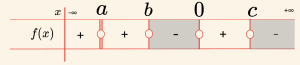
\[\mathcal{Ç} = \{ x \mid x < b \text{ veya } 0 \leq x < c, \, \; x \in \mathbb{R} \} \]
\(\textbf{Cevab: C} \)
← Önceki Sayfa | Sonraki Sayfa →