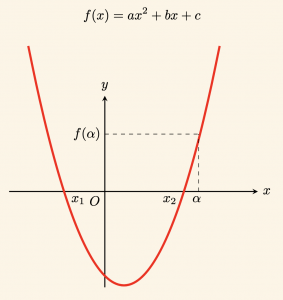
İkinci Dereceden Bir Denklemin Köklerinin Bir Reel Sayıyıla Karşılaştırılması
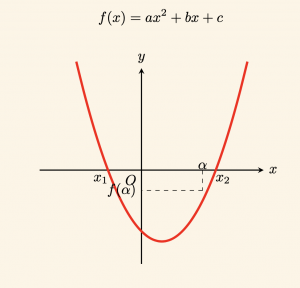
\(f(x) = ax^2 + bx + c\) ikinci dereceden fonksiyonunun grafiğinden (parabol) faydalanarak
\(ax^2 + bx + c = 0\) denkleminin \(x_1,\; x_2\) kökleriyle \(\alpha\) reel sayısını karşılaştıralım.
\(1. \quad \alpha \) kökler arasında ise,
\(a > 0\) için \(x_1 < \alpha < x_2\) ise \(f(\alpha) < 0\) dır. Buradan
\[ a \cdot f(\alpha) < 0\] olur.
Uyarı:
\(f(x) = ax^2 + bx + c = 0\) denklemlerinde \(a \cdot f(\alpha) < 0\) ise \(\Delta > 0\) dır.
Örnek:
\(f(x) = (m – 1)x^2 + (1 – 3m)x + m + 2 = 0\) denkleminin kökleri \(x_1, x_2\) dir.
\(x_1 < 2 < x_2\) ise \(m\)’nin hangi aralıkta olduğunu bulalım.
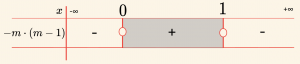
\(x_1 < 2 < x_2\) olması için \(\alpha = m – 1\) ve \(\alpha = 2\) olduğundan
\[m – 1 = 2 \Rightarrow (m – 1)(2 – m) < 0 \quad \text{olmalıdır.} \]
\[
\Rightarrow (m – 1) \cdot \left[ (m – 1) \cdot 2^2 + (1 – 3m) \cdot 2 + m + 2 \right] < 0
\]
\[
\Rightarrow (m – 1) \cdot (-m) < 0
\]
\[
Ç = \{ m \mid m < 0 \text{ veya } m > 1,\ m \in \mathbb{R} \} \text{ olarak bulunur.}
\]
SORU 30
\(f(x) = (m -\; 1)x^2 – (m^2 + 1)x + 2m^2 -\; 6m + 6 = 0\) denkleminin kökleri \(x_1, \;x_2\) dir. \(x_1 < 1 < x_2\) ise \(m\) için aşağıdakilerden hangisi doğrudur?
\[ \text{A) } 4 < m < 5 \quad
\text{B) } -1 < m < 5 \quad
\text{C) }1 < m < 6 \quad
\text{D) } m > 4 \quad
\text{E) } 1 < m < 4 \]
Çözüm:
\(a = m – 1\) ve \(\alpha = 1\) ise,
\[x_1 < 1 < x_2 \Rightarrow (m – 1) \cdot f(1) < 0\]
\[
\Rightarrow (m – 1) \cdot \left[(m – 1) \cdot 1^2 – (m^2 + 1) \cdot 1 + 2m^2 – 6m + 6\right] < 0
\]
\[
\Rightarrow (m – 1) \cdot \left[m – 1 – m^2 – 1 + 2m^2 – 6m + 6 \right] < 0
\]
\[
\Rightarrow (m – 1) \cdot (m^2 – 5m + 4) < 0
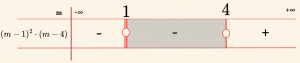
\Rightarrow (m – 1)^2 \cdot (m – 4) < 0
\]
\[
Ç = \{ m \mid m < 1 \text{ veya } 1 < m < 4,\ m \in \mathbb{R} \}
\]
\(\textbf{Cevab: E} \)
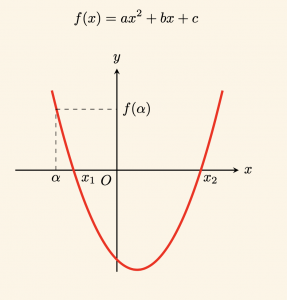
\(2. \quad \alpha \) kökler dışında ise,
\(a > 0 \) için \(\alpha < x_1 < x_2 \) ise \(f(\alpha) > 0 \) olur.
Buradan \(a \cdot f(\alpha) > 0\) olur. O hâlde,
\[
\alpha < x_1 < x_2 \\ \Leftrightarrow
\left\{
\begin{aligned}
\quad &\Delta > 0\\
\quad &a \cdot f(\alpha) > 0 \\
\quad &r = -\frac{b}{2a} > \alpha
\end{aligned}
\right. \\
\]
\(a > 0\) için \(x_1 < x_2 < \alpha\) ise \(f(\alpha) > 0\) olur. Buradan yine \(a \cdot f(\alpha) > 0\) olur. O hâlde:
\[
x_1 < x_2 < \alpha \\ \Leftrightarrow
\left\{
\begin{aligned}
\quad &\Delta > 0\\
\quad &a \cdot f(\alpha) > 0 \\
\quad &r = -\frac{b}{2a} < \alpha
\end{aligned}
\right. \\
\]
Örnek:
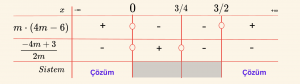
\(f(x) = mx^2 + (2m – 3)x + m – \;3 = 0\) denkleminin kökleri \(x_1, \;x_2\) dir. \(x_1 < x_2 < 1\) ise \(m\)’nin hangi aralıkta olduğunu bulalım.
\(x_1 < x_2 < 1\) olması için,
\[
\Delta = (2m – 3)^2 – 4m \cdot (m – 3) = 9 > 0
\]
\(a = m\), \(\alpha = 1\) ise:
\[
m \cdot f(1) > 0 \Rightarrow m \cdot [m + (2m – 3) + (m – 3)] > 0 \Rightarrow m(4m – 6) > 0
\]
ve
\[
r = \frac{-b}{2a} = \frac{-(2m – 3)}{2m} < 1 \Rightarrow \frac{-4m + 3}{2m} < 0
\]
\[
Ç = \{ m \mid m < 0 \text{ veya } m > \frac{3}{2},\ m \in \mathbb{R} \}
\]
Örnek:
\(f(x) = -x^2 + mx -\; 4 = 0\) denkleminin kökleri \(x_1, \; x_2\) dir. \(2 < x_1 < x_2\) ise \(m\)’nin hangi aralıkta olduğunu bulalım.
\(2 < x_1 < x_2\) olması için:
\[
\Delta = m^2 – \;4 \cdot (-1) \cdot (-4) = m^2 – \;16 > 0
\]
\(a = -1\), \(\alpha = 2\) ise:
\[
-1 \cdot f(2) > 0 \Rightarrow -1 \cdot (-2^2 + 2m – \;4) > 0 \Rightarrow -2m + 8 > 0
\]
ve
\[
r = \frac{-b}{2a} = \frac{-m}{-2} = \frac{m}{2} > 2 \Rightarrow m > 4 \;\; \text{olmalıdır.}
\]
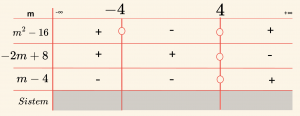
\[ Ç= Ø \]
SORU 31
\(x^2 + mx -\; m – 1 = 0\) denkleminin kökleri \(x_1, \; x_2\) dir. \(x_1 < -1 < x_2 < 2\) ise \(m\) için aşağıdakilerden hangisi doğrudur?
\[ \text{A) } m < -4 \quad
\text{B) } -5 < m < -4 \quad
\text{C) } -4 < m < -3 \quad
\text{D) } -3 < m < 0 \quad
\text{E) } m > 0 \]
Çözüm:
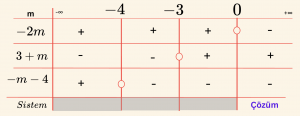
\[f(x) = x^2 + mx – \;m -\; 1\]
\(a = 1\), \(\alpha_1 = -1\), \(\alpha_2 = 2\)
\[x_1 < -1 < x_2 \Rightarrow f(-1) < 0 \Rightarrow 1 \cdot f(-1) < 0 \Rightarrow -2m < 0\]
\[x_1 < x_2 < 2 \Rightarrow f(2) > 0 \Rightarrow 1 \cdot f(2) > 0 \Rightarrow 3 + m > 0\]
\[
r = \frac{-m}{2 \cdot 1} < 2 \Rightarrow -m – 4 < 0
\]
\[
Ç = \{ m \mid m > 0,\ m \in \mathbb{R} \}
\]
\(\textbf{Cevab: E} \)
SORU 32
\(-76x^2 + 19x + 263 = 0\) denkleminin kökleri \(x_1, x_2\) olduğuna göre, aşağıdakilerden hangisi doğrudur?
\[\begin{aligned} \text{A) } x_1 <& 2 < x_2 \quad
\text{B) } x_1 < x_2 < 2 \quad
\text{C) } 2 < x_1 < x_2 \quad \\ \\ \text{D) } &x_1 = x_2 = 2 \quad
\text{E) } x_1 = x_2 < 2 \end{aligned}\]
Çözüm:
\(f(x) = -76x^2 + 19x + 263 = 0\) denkleminin kökleri ile 2 sayısını karşılaştıralım.
\(a = -76\) ve \(\alpha = 2\) ise,
\[
-76 \cdot f(2) = -76 \cdot \left[ -76 \cdot 2^2 + 19 \cdot 2 + 263 \right] = -76 \cdot (-3) > 0
\]
olduğundan 2 kökler dışındadır.
\[
r = \frac{-b}{2a} = \frac{-19}{2 \cdot (-76)} = \frac{1}{8} < 2 \Rightarrow x_1 < x_2 < 2
\]
\(\textbf{Cevab: B} \)
SORU 33
\(m < 0 < n\) olmak üzere,
\(-x^2 + mx + n^2 = 0\) denkleminin kökleri \(x_1, x_2\) olduğuna göre, aşağıdakilerden hangisi doğrudur?
\[
\begin{aligned}
\text{A) }m < n < x_1 < x_2 \\
\text{B) } x_1 < m < n < x_2 \\
\text{C) } x_1 < x_2 < m < n \\
\text{D) } x_1 < m < x_2 < n \\
\text{E) } m < x_1 < n < x_2
\end{aligned}
\]
Çözüm:
\(f(x) = -x^2 + mx + n^2 = 0\) denkleminin kökleri ile m ve n sayılarını karşılaştıralım.
\(a = -1\), \(\alpha_1 = m\), \(\alpha_2 = n\)
\[
-1 \cdot f(m) = -(-m^2 + m \cdot m + n^2) = -n^2 < 0 \Rightarrow m \text{ kökler arasında}
\]
\[
-1 \cdot f(n) = -(-n^2 + m \cdot n + n^2) = -m \cdot n > 0 \Rightarrow n \text{ kökler dışında}
\]
\[
\text{ O halde } \;\; x_1 < m < x_2 < n \;\; \text{olur. }
\]
\(\textbf{Cevab: D} \)
← Önceki Sayfa | Sonraki Sayfa →