Mutlak Değerli ve Köklü Eşitsizlikler
\( 1. \quad g(x) > 0 \) olmak üzere
\[ \left| f(x) \right| < g(x) \quad \text{ ise } \quad -g(x) < f(x) < g(x) \text{ tir.} \]
SORU 18
\[ \left| x^2 – x – 1 \right| < 5 \] eşitsizliğini sağlayan aralıklardan biri aşağıdakilerden hangisidir?
\[ \text{A) } x < -2 \quad
\text{B) } -3 < x < -1 \quad
\text{C) } -2 < x < 3 \quad
\text{D) } x > 3 \quad
\text{E) } 3 < x < 4 \]
Çözüm:
\[\left| x^2 – x – 1 \right| < 5 \Rightarrow -5 < x^2 – x – 1 < 5 \]
\[\Rightarrow -5 < x^2 – x – 1 < 5 \]
\[\Rightarrow -5 < x^2 – x – 1 \quad \text{ve } \quad x^2 – x – 1 < 5 \]
\[ \Rightarrow x^2 – x + 4 > 0 \text{ eşitsizliğinde } a = 1 > 0 \quad \]
ve
\[ \quad \Delta = -15 < 0 \Rightarrow \mathcal{Ç}_1 = \mathbb{R} \]
\[ x^2 – x – 1 < 5 \Rightarrow x^2 – x – 6 < 0 \Rightarrow \text{kökler } x = -2 \text{ ve } x = 3 \]
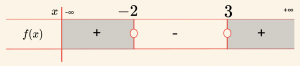
\[ \mathcal{Ç}_2 = \{ x \mid -2 < x < 3, \, x \in \mathbb{R} \} \]
\[ \mathcal{Ç} = \mathcal{Ç}_1 \cap \mathcal{Ç}_2 = \{ x \mid -2 < x < 3, \, x \in \mathbb{R} \} \]
\(\textbf{Cevab: C} \)
SORU 19
\[ \left| x^2 – 3x – 1 \right| < x + 4 \] eşitsizliğini sağlayan aralıklardan birisi aşağıdakilerden hangisidir?
\[\text{A) } -3 < x < -1 \quad
\text{B) } -1 < x < 5 \quad
\text{C) } 5 < x < 7 \quad
\text{D) } x < -3 \quad
\text{E) } x > 7 \]
Çözüm:
\[ x + 4 > 0 \Rightarrow x > -4 \text{ olmak üzere} \]
\[ \left| x^2 – 3x – 1 \right| < x + 4 \]
\[ \Rightarrow -(x + 4) < x^2 – 3x – 1 < x + 4 \]
\[ \Rightarrow -x – 4 < x^2 – 3x – 1 \quad \text{ve} \quad x^2 – 3x – 1 < x + 4 \]
\[ \Rightarrow x^2 – 2x + 3 > 0 \text{ eşitsizliğinde } a = 1 > 0 \text{ ve } \Delta = -8 < 0 \Rightarrow \mathcal{Ç}_1 = \mathbb{R} \]
\[ x^2 – 3x – 1 < x + 4 \] \[\Rightarrow x^2 – 4x – 5 < 0 \]
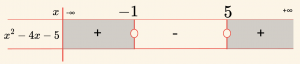
\[ \mathcal{Ç}_2 = \{ x \mid -1 < x < 5, \; x \in \mathbb{R} \} \]
\[ \mathcal{Ç} = \mathcal{Ç}_1 \cap \mathcal{Ç}_2 = \{ x \mid -1 < x < 5, \; x \in \mathbb{R} \} \]
\(\textbf{Cevab: B} \)
\( 2. \quad | f(x) | > g(x) \) ise \( f(x) > g(x) \) veya \( f(x)< -g(x) \) tir.
SORU 20
\( \left| x^2 + x – 5 \right| > 2x + 1 \) eşitsizliğini sağlayan aralıklardan biri aşağıdakilerden hangisidir?
\[ \text{A) } x < 3 \quad
\text{B) } -3 < x < 2 \quad
\text{C) } -1 < x < 3 \quad
\text{D) } x > 3 \quad
\text{E) } x < 2 \]
Çözüm:
\[ \left| x^2 + x – 5 \right| > 2x + 1 \Rightarrow
\begin{cases}
x^2 + x – 5 > 2x + 1 \\
\\
\text{veya} \\
\\
x^2 + x – 5 < -(2x + 1)
\end{cases} \]
\[ \Rightarrow x^2 – x – 6 > 0 \quad \text{veya} \quad x^2 + 3x – 4 < 0 \]
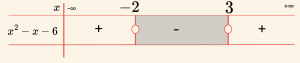
\[ \mathcal{Ç}_1 = \{ x \mid x < -2 \text{ veya } x > 3, \; x \in \mathbb{R} \} \]
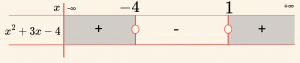
\[ \mathcal{Ç}_2 = \{ x \mid -4 < x < 1, \; x \in \mathbb{R} \} \]
\[ \mathcal{Ç} = \mathcal{Ç}_1 \cup \mathcal{Ç}_2 = \{ x \mid x < 1 \text{ veya } x > 3, \; x \in \mathbb{R} \} \]
\(\textbf{Cevab: D} \)
SORU 21
\( x^2 + x + 4 < \left| -2x^2 + x – 1 \right| < x^2 + x + 9 \) eşitsizliğini sağlayan aralıklardan biri aşağıdakilerden hangisidir?
\[\text{A) } -2 < x < -1 \quad
\text{B) } x < -2 \quad
\text{C) } -1 < x < 3 \quad
\text{D) } x > 3 \quad
\text{E) } 4 < x < 5 \]
Çözüm:
\( -2x^2 + x \;- \; 1 \) üç terimlisinde \( a = -2 < 0 \) ve \( \Delta = -7 < 0 \)
\[ \Rightarrow \forall x \in \mathbb{R} \text{ için } -2x^2 + x – 1 < 0 \;\; \text{dır.} \]
Bu nedenle: \( \left| -2x^2 + x \;- \;1 \right| = 2x^2 \;-\; x + 1 \;\; \) dir. Buna göre eşitsizlik
\[ x^2 + x + 4 < | – 2x^2\; +\; x – 1 | < x^2 + x + 9 \]
\[ \Rightarrow x^2 + x + 4 < 2x^2\; – \;x + 1 \quad \text{ve} \quad 2x^2\; – \;x + 1 < x^2 + x + 9 \]
\[ \Rightarrow -x^2 + 2x + 3 < 0 \quad \text{ve} \quad x^2\; – \;2x \;-\; 8 < 0 \]
Köklere göre işaret tablosu:
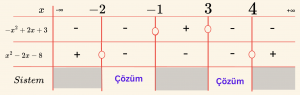
Kesişim: \[ \mathcal{Ç} = \{ x \mid -2 < x < -1 \quad \text{ veya } \quad 3 < x < 4, \; x \in \mathbb{R} \} \]
\(\textbf{Cevab: A} \)
\( 3. \quad | f(x) | < g(x) \) ise \( [f(x)]^2 < [g(x)]^2 \) dir.
SORU 22
\(|x^2 – 3| < |x – 3|\) eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } -4 < x < 1 \quad
\text{B) } 0 < x < 1 \quad
\text{C) } x < -3 \quad
\text{D) } x > 2 \quad d
\text{E) } 1 < x < 2 \]
Çözüm:
\[|x^2 – 3| < |x – 3| \Rightarrow |x^2 – 3|^2 < |x – 3|^2\]
\[\Rightarrow x^4 – 6x^2 + 9 < x^2 – 6x + 9 \]
\[\Rightarrow x^4 – 7x^2 + 6x < 0 \]
\[x^4- 7x^2 +6x = 0 \Rightarrow x(x+3)(x-1)(x-2) =0 \]
\[ x_1= 0 \quad \text{veya } \quad x_2=-3 \quad \text{veya } \quad x_3= 1 \quad \text{ veya } \quad x_4= 2 \]
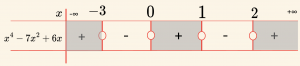
\[ \mathcal{Ç} = \{ x \mid -3 < x < 0 \quad \text{ veya } \quad 1 < x < 2, \; x \in \mathbb{R} \} \]
\(\textbf{Cevab: E} \)
SORU 23
\(|x – 2| – |x + 1| – x + 2 < 0\) eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } -1 < x < 1 \quad
\text{B) } x > 1 \quad
\text{C) } x < -2 \quad
\text{D) } -2 < x < 0 \quad
\text{E) } 0 < x < 3 \]
Çözüm:
Verilen eşitsizlikte mutlak değer içlerinin işaretini inceleyelim.
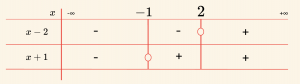
Tabloya göre, \(|x – 2| – |x + 1| – x + 2 < 0\) eşitsizliği,
\(x \leq -1\) için:
\[\begin{aligned} &- (x – 2) – [ – (x + 1) ] – x + 2 < 0 \\
&\Rightarrow -x + 5 < 0 \\
&\Rightarrow x > 5 \;\; \text{ olduğundan } \;\; Ç_1 = Ø
\end{aligned}\]
\(-1 \leq x \leq 2\) için:
\[\begin{aligned}
&- (x – 2) – (x + 1) – x + 2 < 0 \\
&\Rightarrow -3x + 3 < 0 \\
&\Rightarrow x > 1 \;\;\text{ olduğundan } \;\; \\
&Ç_2 = \{x \mid 1 < x \leq 2,\, x \in \mathbb{R}\}
\end{aligned}\]
\(x \geq 2\) için:
\[\begin{aligned}&x – 2 – (x + 1) – x + 2 < 0 \\
&\Rightarrow -x – 1 < 0 \\
&\Rightarrow x > -1 \;\; \text{ olduğundan } \\
&Ç_3 = \{x \mid x \geq 2,\, x \in \mathbb{R}\}
\end{aligned}\]
O halde,
\[
Ç = Ç_1 \cup Ç_2 \cup Ç_3 = \{x \mid x > 1,\, x \in \mathbb{R}\}
\]
\(\textbf{Cevab: B} \)
SORU 24
\[ f(x) = \frac{\sqrt{x + 3} \cdot (x^2 – 16)}{| -x^2 + x + 2 |} < 0 \] eşitsizliğini sağlayan kaç tane \( x \) tam sayı değeri vardır?
\[\text{A) } 5 \quad
\text{B) } 4 \quad
\text{C) } 3 \quad
\text{D) } 2 \quad
\text{E) } 1 \]
Çözüm:
\( x > -3 \) için \( \sqrt{x + 3} > 0 \) olduğundan \( f(x) \)’in işaretini etkilemez.
\( x \ne -1 \) ve \( x \ne 2 \) için \( |-x^2 + x + 2| > 0 \) olduğundan \( f(x) \)’in işaretini etkilemez.
O hâlde \( f(x) \)’in işareti, \( x^2 – 16 \) polinomunun işareti olacaktır.
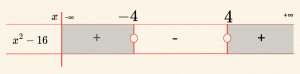
\[
Ç = \{ x \mid -4 < x < 4,\ x \in \mathbb{R} \} \text{ ve}
\]
\( x > -3 \), \( x \ne -1 \) ve \( x \ne 2 \) olduğundan \( x \)’in alabileceği tam sayı değerleri \( -2, 0, 1, 3 \) olup dört tanedir.
\(\textbf{Cevab: B} \)
SORU 25
\[\sqrt[3]{x^3 \;- \;2x^2 + 1} \leq x\; – \;1 \] eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } x < -2 \quad
\text{B) } -2 < x < -1 \quad
\text{C) } -1 < x \leq 1 \quad
\text{D) } 1 \leq x \leq 2 \quad
\text{E) } x \geq 2 \]
Çözüm:
\[
\sqrt[3]{x^3 \; – \; 2x^2 + 1} \leq x \;- \;1
\]
\[
\Rightarrow \left( \sqrt[3]{x^3 \;-\; 2x^2 + 1} \right)^3 \leq (x\; – \;1)^3
\]
\[
\Rightarrow x^3\; – \; 2x^2 + 1 \leq x^3 \;- \;3x^2 + 3x\; – 1
\]
\[
\Rightarrow x^2 \;- \; 3x + 2 \leq 0
\]
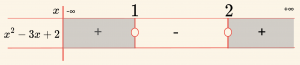
\[
Ç = \{ x \mid 1 \leq x \leq 2,\ x \in \mathbb{R} \} \text{ dir.}
\]
\(\textbf{Cevap: D}\)
SORU 26
\[x – 1 < \sqrt{-x^2 + 3x + 4}\] eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } -1 \leq x < 3 \quad
\text{B) } 0 < x < 4 \quad
\text{C) } 2 < x < 4 \quad
\text{D) } x \geq 3\quad
\text{E) } x < 1 \]
Çözüm:
\( \sqrt{-x^2 + 3x + 4} \) ifadesinin reel sayı belirtmesi için,
\[
– x^2 + 3x + 4 \geq 0 \text{ olmalıdır. O hâlde,}
\]
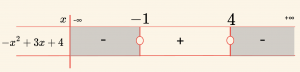
\[
-1 \leq x \leq 4 \text{ olur. Bu durumda,}
\]
\(x – 1 < 0 \Rightarrow x < 1\) için
\[\begin{aligned} &x- 1 < \sqrt{-x^2 + 3x + 4} \quad \text{ eşitsizliği sağlanır ve} \\ & Ç_1 = \{ x \mid -1 \leq x < 1,\ x \in \mathbb{R} \} \quad \text{ dir.}\\
\end{aligned}\]
\(x – 1 \geq 0 \Rightarrow x \geq 1\) için
\[
x – 1 < \sqrt{-x^2 + 3x + 4}
\]
\[ (x – 1)^2 < ( \sqrt{-x^2 + 3x + 4} )^2 \]
\[ \Rightarrow x^2\;-2x+1 < (-x^2 + 3x + 4) \]
\[
\Rightarrow 2x^2 \;- 5x \;-\; 3 < 0
\]
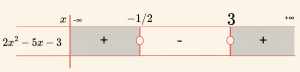
\[
Ç_2 = \{ x \mid 1 \leq x < 3,\ x \in \mathbb{R} \}
\] ve
\[
Ç = Ç_1 \cup Ç_2 = \{ x \mid -1 \leq x < 3,\ x \in \mathbb{R} \} \text{ dir.}
\]
\(\textbf{Cevab: A} \)
SORU 27
\[x + 2 > \sqrt{x^2 \; – 16}\] eşitsizliğini aşağıdaki aralıklardan hangisi sağlar?
\[\text{A) } x < -5 \quad
\text{B) } -5 < x < -4\quad
\text{C) } -4 < x < -2 \quad
\text{D) } -2 < x < 4\quad
\text{E) } x \geq 4 \]
Çözüm:
\[x + 2 > \sqrt{x^2 – 16} \Rightarrow (x + 2)^2 > (\sqrt{x^2 – 16})^2\]
\[
\Rightarrow x^2 + 4x + 4 > x^2 – 16
\]
\[
\Rightarrow 4x + 20 > 0 \text{ olur.}
\]
Ayrıca, \(\sqrt{x^2\; -\; 16}\) ifadesinin reel sayı belirtmesi için
\[
x^2 \; – \;16 \geq 0 \quad \text{ ve } \quad x + 2 > \sqrt{x^2 \; – \;16} \quad \text{ olması için } \quad x + 2 > 0 \text{ olmalıdır.}
\]
O hâlde,
\[
\left.
\begin{aligned}
&4x + 20 > 0 \\ \\
&x^2 – 16 \geq 0 \\ \\
&x + 2 > 0
\end{aligned}
\right\} \quad \text{eşitsizlik sistemi çözülmelidir.}
\]
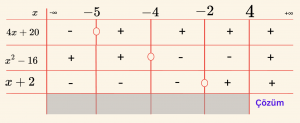
\[
Ç = \{ x \mid x \geq 4,\ x \in \mathbb{R} \} \text{ dir.}
\]
\(\textbf{Cevab: E} \)
SORU 28
\[ \sqrt[x – 1]{2^{x^2 + 5x} }\;\; \geq \;\; 4^x\] eşitsizliğini sağlayan kaç tane \(x\) tam sayı değeri vardır?
\[\text{A) } 4 \quad
\text{B) } 5\quad
\text{C) } 6\quad
\text{D) } 7\quad
\text{E) } 8 \]
Çözüm:
\[\sqrt[x-1]{2x^2 + 5x} \; \geq \; 4^x \Rightarrow 2^{\frac{x^2 + 5x}{x – 1}} \geq 2^{2x}
\]
\[
\Rightarrow \frac{x^2 + 5x}{x – 1} \geq 2x
\]
\[
\Rightarrow f(x) = \frac{-x^2 + 7x}{x – 1} \geq 0
\]
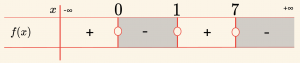
Ayrıca kökün kuvveti olan \(x – 1 \geq 1 \Rightarrow x \geq 2\) ve \(x \in \mathbb{Z}\) olmalıdır.
O hâlde,
\[
Ç = \{ x \mid 2 \leq x \leq 7,\ x \in \mathbb{Z} \} \text{ olur.}
\]
\(x\)’in alabileceği tam sayı değerleri \(2, 3, 4, 5, 6, 7\) olup altı tanedir.
\(\textbf{Cevab: C} \)
← Önceki Sayfa | Sonraki Sayfa →