İki Parabolün Birbirine Göre Durumu
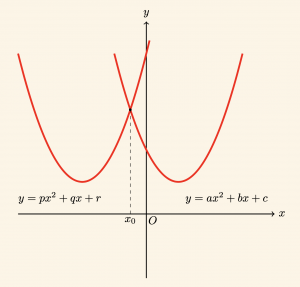
Denklemleri \( y = ax^2 + bx + c \) ve \( y = px^2 + qx + r \) olan iki parabolün birbirine göre durumunu incelemek için
iki parabolün denklemi ortak çözülür.
1) \( a = p \) ve \( b \ne q \) ise,
İki parabol tek noktada kesişir.
\[
\left.
\begin{aligned}
y &= ax^2 + bx + c \\
y &= px^2 + qx + r
\end{aligned}
\right\}\]
\[\Rightarrow ax^2 + bx + c = px^2 + qx + r \]
\[\Rightarrow bx + c = qx + r\]
denkleminin kökü parabollerin kesim noktasının apsisidir.
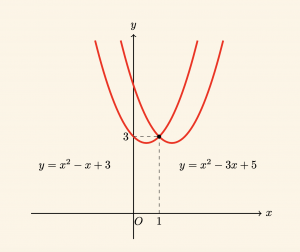
Örnek:
\( y = x^2 – x + 3 \) parabolü ile \( y = x^2 – 3x + 5 \) parabolünün birbirine göre durumunu inceleyelim.
\[
\left.
\begin{aligned}
y &= x^2 – x + 3 \\
y &= x^2 – 3x + 5
\end{aligned}
\right\}
\Rightarrow x^2 – x + 3 = x^2 – 3x + 5 \]
\[\Rightarrow x = 1 \]
olduğundan paraboller tek noktada kesişir. Bu noktanın ordinatını bulalım.
\[ y = x^2\; – \;x + 3 \;\;\text{de} \quad x = 1 \quad \text{için} \quad y = 3 \;\; tür.\]
2) \( \quad a \ne p \) ise,
İki parabolün birbirine göre üç durumu vardır. Bu durumlar incelenirken takip edilecek yol, bir parabol ile bir doğrunun birbirine göre durumunun incelenmesinde izlenen yol ile aynıdır.
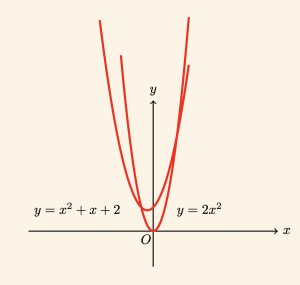
Örnek:
\( y = 2x^2 \) parabolü ile \( y = x^2 + x + 2 \) parabolünün birbirine göre durumunu inceleyelim.
\[
\left.
\begin{aligned}
y &= 2x^2 \\
y &= x^2 + x + 2
\end{aligned}
\right\}
\Rightarrow 2x^2 = x^2 + x + 2 \]
\[\Rightarrow x^2 – x – 2 = 0 \]
\[ \Rightarrow x_1 = -1 \quad \text{ veya } \quad x_2 = 2 \]
olduğundan paraboller iki noktada kesişir. Bu noktaların ordinatlarını bulalım.
\[ y = 2x^2 \; \; \text{de} \]
\[x_1 = -1 \quad \text{için} \quad y_1 = 2 \]
\[ x_2 = 2 \quad \text{için} \quad y_2 = 8 \;\; \text{dir.} \]
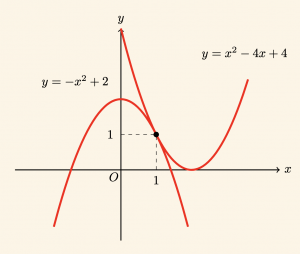
Örnek:
\( y = x^2 – 4x + 4 \) parabolü ile \( y = -x^2 + 2 \) parabolünün birbirine göre durumunu inceleyelim.
\[
\left.
\begin{aligned}
y &= x^2 – 4x + 4 \\
y &= -x^2 + 2
\end{aligned}
\right \}
\Rightarrow x^2 – 4x + 4 = -x^2 + 2 \]
\[ \Rightarrow 2x^2 – 4x + 2 = 0 \]
\[ \Rightarrow x_1 = x_2 = 1 \]
olduğundan paraboller teğettir. Bu noktanın ordinatını bulalım.
\[ y= -x^2 + 2 \;\; \text{de } \quad x= 1 \quad \text{için } \quad y= 1 \;\; \text{dir. } \]
Örnek:
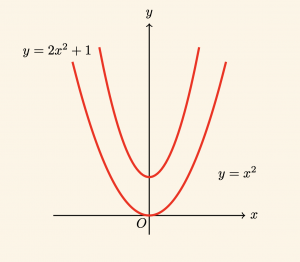
\( y = 2x^2 + 1 \) parabolü ile \( y = x^2 \) parabolünün birbirine göre durumunu inceleyelim.
\[
\left.
\begin{aligned}
y &= 2x^2 + 1 \\
y &= x^2
\end{aligned}
\right\}
\Rightarrow 2x^2 + 1 = x^2 \]
\[\Rightarrow x^2 + 1 = 0\]
\[\Rightarrow \Delta < 0 \]
olduğundan parabollerin ortak noktaları yoktur.
SORU 15
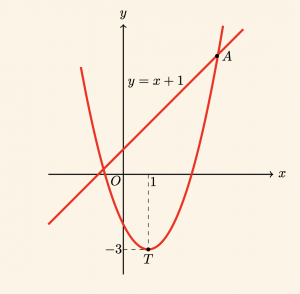
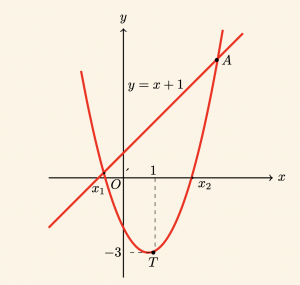
Yandaki şekilde parabolün tepe noktası \( T \) olduğuna göre, A noktasının apsisi nedir?
\[
\text{A)} 7 \quad
\text{B) } 6 \quad
\text{C) } 5 \quad
\text{D) } 4 \quad
\text{E) } 3
\]
Çözüm:
\( y = x + 1 \) doğrusunun Ox eksenini kestiği noktanın apsisi,
\[
y = 0 = x + 1 \Rightarrow x_1 = -1 \text{ dir.}
\]
\[
r = \frac{x_1 + x_2}{2} \Rightarrow 1 = \frac{-1 + x_2}{2} \Rightarrow x_2 = 3 \text{ olur.}
\]
Parabolün denklemi,
\[ y = a(x – x_1)(x – x_2) \;\; \text{den } \]
\[ y = a(x + 1)(x – 3) \]
ve burada \( (0, -3) \) noktası yerine yazılırsa
\[
x = 0 \text{ için } y = -3 = a(0 + 1)(0 – 3) \Rightarrow a = 1
\]
olduğundan
\[ y = (x + 1)(x – 3) = x^2 – 2x – 3 \quad \text{bulunur. } \]
Parabol ile doğrunun denklemini ortak çözelim.
\[
\left.
\begin{aligned}
y &= x^2 – 2x – 3 \\
y &= x + 1
\end{aligned}
\right\}
\Rightarrow x^2 \;-\; 2x\; -\; 3 = x + 1 \]
\[\Rightarrow x = -1 \text{ veya } x = 4 \text{ tür.}
\]
O halde A noktasının apsisi 4 tür.
\(\textbf{Cevab: D} \)
SORU 16
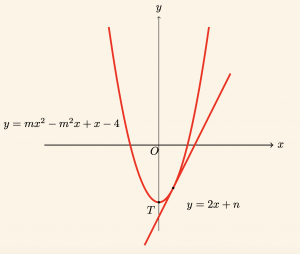
Aşağıdaki şekilde\( y = 2x + n \) doğrusu, tepe noktası Oy ekseni üzerinde olan \( y = mx^2 – m^2x + x – 4m \)
parabolüne teğettir.
Buna göre, \( n \) kaçtır?
\[
\text{A)} -5 \quad
\text{B) } -6 \quad
\text{C) } -7 \quad
\text{D) } -8 \quad
\text{E) } -9
\]
Çözüm:
\[
y = mx^2 – m^2x + x – 4m \]
\[\Rightarrow y = mx^2 + (1 – m^2)x – 4m
\]
Parabolün tepe noktası Oy ekseni üzerinde olduğundan,
\[
1 – m^2 = 0 \Rightarrow m = -1 \text{ veya } m = 1 \text{ olur.}
\]
Parabolün kolları Oy ekseninin pozitif yönünde olduğundan \( m = 1 \) ve \( y = x^2 – 4 \) tür.
O halde parabol ile doğrunun denklemlerini ortak çözelim.
\[
\left.
\begin{aligned}
y &= x^2 – 4 \\
y &= 2x + n
\end{aligned}
\right\}
\Rightarrow x^2 – 4 = 2x + n \]
\[\Rightarrow x^2 – 2x – 4 – n = 0
\]
ve doğru, parabole teğet olduğundan,
\[ \Delta = (-2)^2 – 4 \cdot 1 \cdot (-4 – n) = 0 \]
\[ \Rightarrow 4 + 16 + 4n = 0 \]
\[ \Rightarrow n = -5 \text{ dir.} \]
\(\textbf{Cevab: A} \)
SORU 17
\( y = -x^2 – x + 2 \) parabolünün \( y = -2x + 3 \) doğrusuna en yakın noktasının ordinatı nedir?
\[
\text{A)} \frac{3}{4} \quad
\text{B) } 1 \quad
\text{C) } \frac{5}{4} \quad
\text{D) } \frac{3}{2} \quad
\text{E) } \frac{7}{4}
\]
Çözüm:
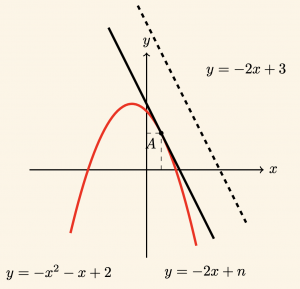
Parabol üzerindeki A noktası, \( y = -2x + 3 \) doğrusuna en yakın nokta olsun. Parabolün A noktasındaki teğeti
\( y = -2x + 3 \) doğrusuna paralel olacağından, denklemi \( y = -2x + n \) şeklindedir.
Bu denklem, parabolün denklemi ile ortak çözülürse
\[
\left.
\begin{aligned}
y &= -x^2 – x + 2 \\
y &= -2x + n
\end{aligned}
\right\}
\Rightarrow -x^2 – x + 2 = -2x + n \]
\[ \Rightarrow x^2 – x + n – 2 = 0 \]
ve doğru, parabole teğet olduğundan kökler çakışık (\( \Delta = 0 \)) olmalıdır.
O halde,
\[
x_1 = x_2 = \frac{-b}{2a} = \frac{1}{2}
\]
kökü A noktasının apsisidir.
Bu noktanın ordinatı, \[ y = -x^2 – x + 2 \quad \text{de} \quad x = \frac{1}{2} \;\; \text{için } \]
\[
y = -\left(\frac{1}{2}\right)^2 – \frac{1}{2} + 2 = \frac{5}{4} \text{ tür.}
\]
\(\textbf{Cevab: C} \)
SORU 18
\( y = 2x^2 + 6x + m \) parabolü ile \( y = x^2 + 2x – m \) parabolü birbirine teğet ise değme noktasının apsisi ile \( m \)’nin toplamı nedir?
\[
\text{A)} -3 \quad
\text{B) } -2 \quad
\text{C) }-1\quad
\text{D) } 0 \quad
\text{E) } 1
\]
Çözüm:
Parabollerin denklemlerini ortak çözelim:
\[
\left.
\begin{aligned}
y &= 2x^2 + 6x + m \\
y &= x^2 + 2x – m
\end{aligned}
\right\}
\Rightarrow 2x^2 + 6x + m = x^2 + 2x – m\]
\[\Rightarrow x^2 + 4x + 2m = 0 \]
ve iki parabol teğet olduğundan,
\[
\Delta = 4^2 – 4 \cdot 1 \cdot 2m = 0 \Rightarrow m = 2 \quad \text{ olur.}
\]
Bu değer yukarıda elde edilen denklemde yerine yazılırsa,
\[
x^2 + 4x + 2m = 0 \Rightarrow x^2 + 4x + 4 = 0 \]
\[\Rightarrow x_1 = x_2 = -2 \]
değme noktasının apsisidir.
O halde \( -2 + 2 = 0 \) dır.
\(\textbf{Cevab: D} \)
SORU 19
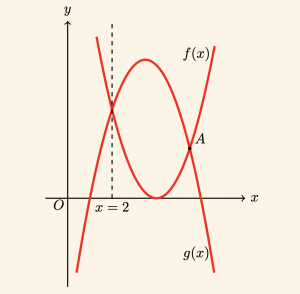
Yukarıdaki şekilde \( f(x) = mx^2 – 8x + 8m + 8 \) parabolü ile \( g(x) = -x^2 + (3m + 4)x – 5m – 1 \) parabolleri verilmiştir. A noktasının apsisi nedir?
\[
\text{A)} \frac{11}{2} \quad
\text{B) } 6 \quad
\text{C) } \frac{13}{2} \quad
\text{D) } 7 \quad
\text{E) } 8
\]
Çözüm:
Paraboller \( x = 2 \) doğrusu üzerinde kesiştiğine göre,
\[
\left.
\begin{aligned}
f(2) &= 12m – 8 \\
g(2) &= m + 3
\end{aligned}
\right \}
\quad \text{ve} \quad f(2) = g(2)
\Rightarrow 12m – 8 = m + 3 \]
\[ \Rightarrow m = 1 \;\; \text{ olur.} \]
Bu değeri parabollerin denkleminde yerine yazarak denklemleri ortak çözelim.
\[\left.
\begin{aligned}
f(x) &= x^2 – 8x + 16 \\
g(x) &= -x^2 + 7x – 6
\end{aligned}
\right \}
\Rightarrow f(x) = g(x)
\Rightarrow 2x^2 – 15x + 22 = 0 \]
\[ \Rightarrow x = 2 \quad \text{ veya } \quad x = \frac{11}{2} \]
olduğundan A noktasının apsisi \[ \frac{11}{2} \] dir.
\(\textbf{Cevab: A} \)
SORU 20
\( m \)’nin değişen değerleri için,
\[
f(x) = (m + 1)x^2 + (m + 2)x – 2m + 1 \]
ve
\[ g(x) = mx^2 + 3mx – m^2
\]
parabolleri veriliyor. f(x) ve g(x) parabol çiftleri için aşağıdakilerden hangisi doğrudur?
\[
\begin{aligned}
&\text{A)} \text{Farklı iki noktada kesişirler. } \quad \\
&\text{B) } \text{Teğettirler. } \quad \\
&\text{C) } \text{Tek noktada kesişirler. } \\
&\text{D) } \text{Ortak noktaları yoktur. } \\
&\text{E) } \text{Çakışıktırlar.} \\
&\end{aligned}
\]
Çözüm:
\( f(x) \) parabolü ile \( g(x) \) parabolünün denklemlerini ortak çözelim:
\[
f(x) = (m + 1)x^2 + (m + 2)x – 2m + 1 \]
\[
g(x) = mx^2 + 3mx – m^2
\]
\[
\Rightarrow f(x) = g(x) \text{ eşitliği düzenlenirse,} \]
\[\Rightarrow x^2 + (2 – 2m)x + m^2 – 2m + 1 = 0 \]
\[
\Rightarrow \Delta = (2 – 2m)^2 – 4 \cdot 1 \cdot (m^2 – 2m + 1) = 0
\]
olduğundan teğettirler.
\(\textbf{Cevab: B} \)
SORU 21
\( m \)’nin değişen değerleri için,
\[
y = x^2 + (2m + 4)x + 2m + 5
\]
parabollerinin geçtiği sabit bir nokta vardır. Bu noktanın apsisi nedir?
\[
\text{A)} 2 \quad
\text{B) } 1 \quad
\text{C) } 0 \quad
\text{D) } -1 \quad
\text{E) } -2
\]
Çözüm:
Bu parabollerden iki tanesini seçip ortak çözüm yapalım.
\[
y = x^2 + (2m + 4)x + 2m + 5 \text{ ise,}
\]
\[
\begin{aligned}
m = 1 &\Rightarrow y = x^2 + 6x + 7 \\
m = 2 &\Rightarrow y = x^2 + 8x + 9
\end{aligned}
\]
\[
x^2 + 6x + 7 = x^2 + 8x + 9
\Rightarrow x = -1 \text{ dir.}
\]
\(\textbf{Cevab: D} \)
← Önceki Sayfa | Sonraki Sayfa →