Parabolün Denklemini Bulma

1) $ \quad y = ax^2 + bx + c $

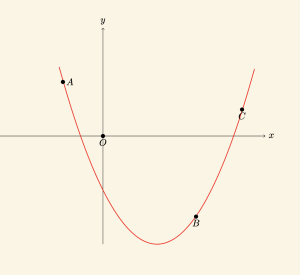
Parabolü üzerindeki herhangi üç nokta biliniyorsa, bu noktalar parabolün denkleminde yerine yazılarak $a, b, c$ katsayıları elde edilir ve parabolün denklemi bulunur.

Örnek:

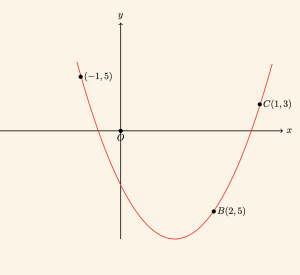
Yandaki şekilde verilen parabolün denklemini bulalım. Parabol üzerindeki noktalar,

\[
y = ax^2 + bx + c
\]

parabol denkleminde yerine yazılırsa,

$ A(-1 , 5) $ için $ a – b + c = 5 $,

$B(2 , 5) $ için $ 4a + 2b + c = 5 $ ve

$ C(1 , 3) $ için $ a + b + c = 3 $ denklemleri elde edilir.

Ortak çözüm yapılırsa,

\[ a = 1, \quad b = -1 \quad \text{ve } c = 3 \quad \text{olur} \]

O halde;

\[ y = ax^2 + bx + c \Rightarrow y = x^2 – x + 3 \]

2) Parabol üzerindeki herhangi bir nokta ile parabolün Ox eksenini kestiği noktalar biliniyorsa, parabolün denklemi,

\[ y = a(x – x_1)(x – x_2) \]

ifadesi kullanılarak bulunur.

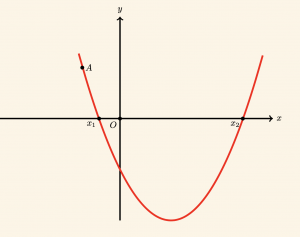
Örnek:

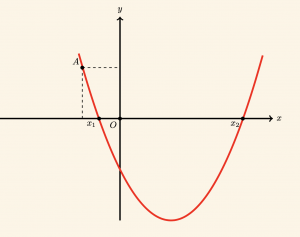
Yukarıdaki şekilde verilen parabolün denklemini bulalım. Parabolün Ox eksenini kestiği noktaların apsisleri

\[ x_1 = -1 \quad \text{ve } x_2 = 2 \quad \text{olduğundan,} \]

\[ y = a(x + 1)(x – 2) \]

ifadesinden

\[ y = a(x + 1)(x – 2) \] elde edilir.

Burada $ a $’yı bulmak için parabol üzerindeki $ (-2, \frac{5}{3}) $ noktası, elde edilen parabol denkleminde yerine yazılırsa,

$ x = -2 $ için $ y = \frac{5}{3} = a(-2 + 1)(-2 – 2) $

\[ \Rightarrow a = \frac{5}{12} \quad \text{ve } y = \frac{5}{12} (x + 1)(x – 2) \quad \text{dir.} \]

3) Parabol üzerindeki herhangi bir nokta ile parabolün tepe noktası biliniyorsa, bu parabolün denklemi,

\[ y = a(x – r)^2 + k \]

ifadesi kullanılarak bulunur.

Örnek:

Yandaki şekilde verilen tepe noktası T olan parabolün denklemini bulalım.

Parabolün tepe noktasının koordinatları:

\[ r = -1 \quad \text{ve } \quad k = 4 \quad \text{olduğundan, } \]

\[ y = a(x – r)^2 + k \quad \text{ifadesinden } \quad y = a(x + 1)^2 + 4 \quad \text{elde edilir.} \]

Burada $ a $’yı bulmak için parabol üzerindeki $ (0, 3) $ noktası, elde edilen parabol denkleminde yerine yazılırsa,

\[ x = 0 \quad \text{için} \quad y = 3 = a(0 + 1)^2 + 4 \]

\[ \Rightarrow a = -1 \quad \text{ve } y = -(x + 1)^2 + 4 \quad \text{tür. } \]

SORU 13

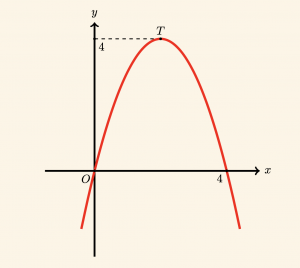
Yukarıdaki şekilde tepe noktası T olan $ y = f(x) $ parabolü orijinden geçtiğine göre, $ f(5) $ kaçtır?

\[
\text{A)} -6 \quad
\text{B) } -5 \quad
\text{C) } -4 \quad
\text{D) } -3 \quad
\text{E) } -2
\]

Çözüm:

Parabolün Ox eksenini kestiği noktaların apsisleri

\[ x_1 = 0 \quad \text{ve } \quad x_2 = 4 \quad \text{olduğundan, } \]

\[ y = a(x – x_1)(x – x_2) \Rightarrow y = a x (x – 4) \] ve parabolün tepe noktasının apsisi de

\[
r = \frac{x_1 + x_2}{2} \Rightarrow r = \frac{0 + 4}{2} = 2 \text{ olur.}
\]

Ayrıca $ T(2, 4) $ noktası parabolün denkleminde yerine yazılırsa,

\[ x = 2 \quad \text{için} \quad y = 4 = a \cdot 2 \cdot (2 – 4) \]

\[ \Rightarrow a = -1 \quad \text{ve } f(x) = -x(x – 4) \quad \text{bulunur.} \]

O halde $ f(5) = -5(5 – 4) = -5 $ tir.

$\textbf{Cevab: B} $

SORU 14

Yandaki şekilde tepe noktası $ T(-2, -1) $ olan parabol verilmiştir. ATB üçgeninin alanı kaç birim karedir?

\[
\text{A)} 1 \quad
\text{B) } 2 \quad
\text{C) } 3 \quad
\text{D) } 4 \quad
\text{E) } 5
\]

Çözüm:

Parabolün tepe noktasının koordinatları $ r = -2 $ ve $ k = -1 $ olduğundan,

\[
y = a(x – r)^2 + k \Rightarrow y = a(x + 2)^2 – 1 \text{ olur.}
\]

Ayrıca $ (0, 3) $ noktası parabolün denkleminde yerine yazılırsa,

\[
x = 0 \text{ için } y = 3 = a(0 + 2)^2 – 1
\]

\[
\Rightarrow a = 1 \text{ ve } y = (x + 2)^2 – 1
\]

bulunur. O halde, parabolün eksenleri kesim noktalarını bulalım.

\[
y = (x + 2)^2 – 1 = 0 \Rightarrow x^2 + 4x + 3 = 0
\]

\[
\Rightarrow x = -3 \text{ veya } x = -1
\]

\[
\Rightarrow A(-3, 0) \text{ ve } B(-1, 0)
\]

olduğundan,

\[
A(ATB) = \frac{ |AB| \cdot |k| }{2} = \frac{2 \cdot |-1|}{2} = 1 \text{ birim karedir.}
\]

$\textbf{Cevab: A} $